初三数学动手操作与应用训练题（一）
班级＿＿＿＿ 姓名＿＿＿＿ 得分＿＿＿＿
1．如图，边长为12米的正方形池塘的周围是草地，池塘边A、B、C、D处各有一棵树，且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大，应将绳子拴在（ ）.
| （A）A处 | （B）B处 | （C）C处 | （D）D处 |
2. 都江堰市将前市委书记挪用公款修建的11套价值400万元的别墅公开拍卖了。如果一个家庭3个人，人均住房面积按25平方米，每平方米1000~1200元计算，那么这11套别墅的价值至少可解决（ ）家庭的住房问题。
（A）30多个 （B）40多个 （C）50多个 （D）60多个
3. 如图为某种汽车的一种平顶内藏式的矩形天窗，天窗的长为862mm，宽为475mm．若设天窗打开的宽度为xmm，则天窗打开部分的面积s（
）与打开的宽度x（mm）之间的函数关系式（要求天窗必须打开）是________________
（写出自变量x的取值范围）．
4. 某天清晨，小鹏同学生病了，体温上升，吃过药后感觉好多了，中午时他的体温基本正常，但是下午他的体温又开始上升，直到半夜才感觉身上不那么发烫了. 下面大致能上反映出小鹏这一天（0时—24时）体温的变化情况的图是（ ）
 |
（A） （B） （C） （D）
5．用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.
 |
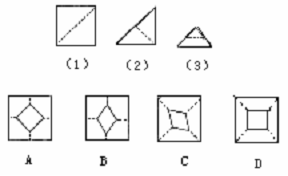6．小强拿了一张正方形的纸如图（1），沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是（ ）
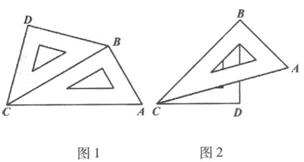
7．将一副三角板如示意图摆放在一起，请在图1或图2中任选一个图形进行解答。
（1）连结DA，计算∠BDA的余切值；（2）求作一个二次项系数为1的一元二次方程，使cot∠BDA和2tan∠BDA为此方程的两个根。
8.已知A（1，2），B（-2，5），要求写出一个二次函数使其图象经过A、B两点，甲、乙两个学生展开了如下讨论：
甲：再自己任意给定一个点的坐标，便可通过待定系数法求得
乙：这种方法当然可行。若要求写出两个、三个或更多的满足条件的二次函数解析式，按你这种做法太麻烦。能不能找到一个更好的办法呢？
（甲、 乙两人陷入了沉思……）
乙：我有了个想法！即便要写更多个比你这种方法方便得多！
甲：请多多指教！
乙：……
问：请你说说更方便的做法。
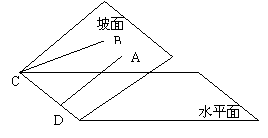
9.人们拖着一辆沉重的板车爬上一个陡坡，感到十分吃力。为了省力，采用沿着坡面斜着向上拖。如图，沿CB而不沿DA拖。请你用数学的原理解释其合理性。
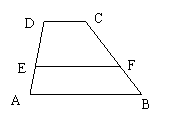
10．如图，在梯形ABCD中AB∥CD ，CD=a，AB=b，E为AD边上的一点，EF∥AB，且EF交BC于点F.
（1）某学生在研究这一问题时，发现如下事实：
①当
时，有
；
②当
时，有
；
③当
时，有
；……
当
时，有，参照上述研究结论，请你猜想用a、b和k表示EF的一般结论：
.
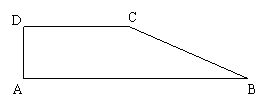（2）现有一块直角梯形田地（如图所示），其中AB∥CD，AD⊥AB，AB=310米，AD=70米.若要将这块地方割成两块，由两农民来承包.要求这两块地均为直角梯形，且面积相等.请你给出具体分割方案.