初三数学月考
试题
(满分150分,120分钟完卷)
学校 姓名
一、选择题(4分×6=24分)
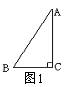 1、如图1,在△ABC中,∠C=900,a、b分别为∠A、∠B的对边,比值
1、如图1,在△ABC中,∠C=900,a、b分别为∠A、∠B的对边,比值![]() 是∠A的( )
是∠A的( )
A、正弦 B、余弦 C、正切 D、余切
2、下列命题中真命题的( )
A、平分弦的直径垂直于弦 B、垂直于半径的直线是圆的切线
C、同圆中较大的弦的弦心距小 D、三点确定一个圆
3、方程3x2=0与5x2 =5x的解是( )
A、都是x =0 B、有一个相同的解为0 C、都不相同 D 以上都不对
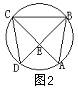 4、如图2,弦AC、BD交于点E,且
4、如图2,弦AC、BD交于点E,且![]() =
=![]() =
=![]() ,若∠ACD=300,则∠AED=( )
,若∠ACD=300,则∠AED=( )
A、800 B、900 C、1000 D、1100
5、若ab>0、ac<0,那么y=![]() x+
x+![]() 的图象经过( )
的图象经过( )
A、第一、二、三象限 B、第一、二、四象限
C、第一、三、四象限 D、第二、三、四象限
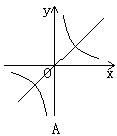
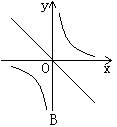
6、如图,在同一坐标系中,正比例函数y=(a-1)x与反比例函数y=![]() 的图象的大致位置不可能是( )
的图象的大致位置不可能是( )
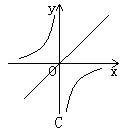
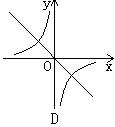
二、填空题(4分×10=40分)
7、当a 时,方程(a2-1)x2+(a-3)x +a=0是一元二次方程。
8、Rt△的两直角边为5、12,则其外接圆半径为 ,内切圆半径为 。
9、函数y=(x+2)0-![]() 的自变量x的取值范围是
。
的自变量x的取值范围是
。
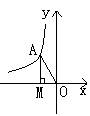 10、圆内的两条平行弦长分别为6和8,半径为5,则这两条弦间的距离为
。
10、圆内的两条平行弦长分别为6和8,半径为5,则这两条弦间的距离为
。
11、一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O为原点,如果S△AOM=3,那么这个反比例函数的解析式为 。
12、圆心都在y轴上的两圆相交于A、B两点,如果A的坐标为(2,![]() ),那么点B的坐标是
。
),那么点B的坐标是
。
13、在直角坐标系中,分别以点A(0,3)与点B(4,0)为圆 心,以8与3为半径作⊙A和⊙B,则这两个圆的位置关系为
14、已知等腰三角形面积为4![]() ㎝2,一腰上的高为2
㎝2,一腰上的高为2![]() ㎝,则这条高与底边的夹角为
。
㎝,则这条高与底边的夹角为
。
 15、规定i2=-1,则方程x2=-1可写成x2=
i2,所以x=
15、规定i2=-1,则方程x2=-1可写成x2=
i2,所以x=![]() i,知道i1=i ,i2=-1, i3=-i, i4=1,i5= i,i6=-1,i7 =- i,i8=1…通过观察知道i2005=
。
i,知道i1=i ,i2=-1, i3=-i, i4=1,i5= i,i6=-1,i7 =- i,i8=1…通过观察知道i2005=
。
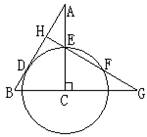
16、如图,在△ABC中,∠ACB=900,以顶点C为圆心的圆切AB于点D,交AC于点E,过点E作AB的垂线,垂足为H,HE交BC的延长线于点G,已知∠A=300,AE=25,则EG= 。
三、解答题
17、计算(![]() -1)0-
-1)0-
![]() +(sin300)-2+3tan600 (6分)
+(sin300)-2+3tan600 (6分)
18、解方程(组)(6分×2=12分)
(1)3x3-5x2+2x=0
(2) ![]()
19、已知:如图⊙O的弦AB=2![]() ㎝,半径OC⊥AB于M,
㎝,半径OC⊥AB于M,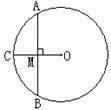 若CM=1㎝,求OM的长。( 6分)
若CM=1㎝,求OM的长。( 6分)
20、已知关于x的一元二次方程(k-3)x2-![]() x+1=0有两个不相等的实数根,求k的取值范围。( 6分)
x+1=0有两个不相等的实数根,求k的取值范围。( 6分)
21、已知如图,两点A(-8,0),B(2,0),以AB为直径的半圆与y轴正半轴交于点C。(8分)
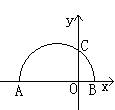 ①求过点A、C的直线的解析式和过A、B、C三点的抛物线的解析式;
①求过点A、C的直线的解析式和过A、B、C三点的抛物线的解析式;
②抛物线的顶点,求D点的坐标。
22、(1)已知反比例函数y=![]() ,当x=-
,当x=-![]() 时,y=-6,求出这个解析式;(3分)
时,y=-6,求出这个解析式;(3分)
(2)若一次函数y=mx-4的图象与(1)中的反比例函数y=![]() 的图象有交点,求m的取值范围。(4分)
的图象有交点,求m的取值范围。(4分)
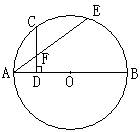
23、如图,AB为⊙O的直径,C为 ![]() 的中点,CD⊥AB于点D,与AE相交于点F。求证:①AD·AB=AF·AE ②AF=CF (10分)
的中点,CD⊥AB于点D,与AE相交于点F。求证:①AD·AB=AF·AE ②AF=CF (10分)
24、某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售y件之间有如下关系:
| X | 3 | 5 | 9 | 11 |
| y | 18 | 14 | 6 | 2 |
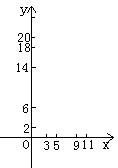
根据表中提供的数据
(1)在右图直角坐标系中描出实数对(x,y)的对应点;(3分)
(2)猜测并确定日销售量y件与日销售单价x元之间的函数关系式,并在右图中画出图象;(4分)
(3)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售规律,试求出日销售利润P元与日销售单价x元之间的函数关系式,并求出日销售单价x为多少元时,才能获得最大日销售利润。(5分)
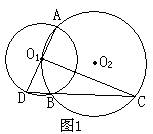
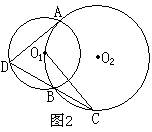
25、已知⊙O1与⊙O2相交于A、B两点,且O2在⊙O1上。⑴如图一,AD是⊙O2的直径,连结DB并延长交⊙O1于点C,求证:C O2⊥AD;⑵如图二,AD是⊙O2的一条弦,连结DB并延长交⊙O1于点C,这时C O2所在直线是否仍与AD垂直?请证明你的结论。(11分)
26、已知二次函数y=x2-(m2+5)x+2m2+6(x为自变量)的图象与x轴交于A(2,0)、B两点,与y轴交于C点,且A、B两点间的距离为8。(11分)
(1)求这个二次函数的解析式。
(2)画出这个二次函数的图象(草图),若二次函数的图象的顶点坐标为P。求△PAC的面积。