初三数学月考试卷3
一、选择题（每小题4分，共48分）
1．下列各式不是单项式的是（ ）．
A．4x2 B．a C．－1 D．5m —1
2．若不等式2x-m≤0的正整数解为1,2,3,则字母m的取值范围是 ( )
A． m≥6 B .m＜8 C .6≤m＜8 D .6＜m≤8
3．如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，
使其不变形，这样做的根据是（ ）．
A．两点之间的线段最短 B．长方形的四个角都是直角
C．长方形是轴对称图形 D．三角形有稳定性
4．从等腰三角形底边上任意一点分别作两腰的平行线，那么所成的平行
四边形的周长等于这个等腰三角形的（ ）
A.周长 B.周长的一半 C. 腰长 D.腰长的二倍 （第3题图）
5．下图是各种汽车的标志，其中是轴对称图形的有（ ）个．
A．1个 B．2个 C．3个 D．4个
6、如图，下图是汽车行驶速度（千米／时）和时间（分）
的关系图，下列说法其中正确的个数为（ ）
（1）汽车行驶时间为40分钟；
（2）AB表示汽车匀速行驶；
（3）在第30分钟时，汽车的速度是90千米／时； （第6题图）
（4）第40分钟时，汽车停下来了．
A．1个 B．2个 C．3个 D．4个
7．小华利用计算器计算0.×0.时，
发现计算器的显示屏上显示如右图的结果，对这个结果
表示正确的解释应该是（ ）．
A．1.677025×10—14 B．1.677025×1014 （第7题图）
C．（1.677025×10）—14 D．1.677025×10×（—14）
8．下面给出的事件中，概率为1的事件有（ ）个．
（1）打开电视机，正在播放新闻；
（2）太阳每天从东方升起；
（3）“非典型性肺炎”病毒最终一定会被人类征服；
（4）人体吸入大量煤气（一氧化碳）会中毒．
A．0个 B．1个 C．2个 D．3个
9．如图，光线a照射到平面镜CD上，然后在平面镜 （第10题图）
AB和CD之间来回反射，这时光线的入射角等于反射角，即∠1＝∠6，
∠5＝∠3，∠2＝∠4。若已知∠1=55°，∠3=75°，那么∠2等与（ ）
A．50° B．55° C．66° D．65°
10.下列等式中，计算正确的是（ ）
A．
B．
C．
D．
（A） 
（B） 3 （C）
（D）-3
12.在平地上投掷手榴弹,下面哪幅图可以大致刻画出手榴弹投掷过程中(落地前)速度变化情况( )
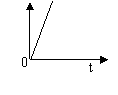
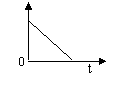
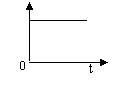
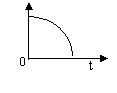v
v
v
v
A B C D
二、填空题（每小题3分，共24分）
13．多项式3x3y —2xy＋2的次数是 ．
14．要从一张长为40cm、宽为20cm的长方形纸片（如图）中，
剪出长为18cm、宽为12cm的长方形 纸片，则最多能剪
出 张． （第12题图）
15．在直角三角形、钝角三角形和锐角三角形这三种三角形中，
有两条高在三角形外部的是 三角形．
16．把一副常用的三角板如图所示拼在一起，那么图中∠ADE
是 度．
17.若
，那么m=________
18.如图：△ABC平移到△DEF，则图中与线段AD平行且相等的
线段有 条.
20.在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）。
把余下的部分剪拼成一个矩形（如图）。通过计算图形
（阴影部分）的面积，验证了一个等式，则这个等式是
三、解答题（共78分）
15．计算：
．
16．求值：
．
 |
17.求不等式组 的自然数解;
18．阅读下列因式分解的过程，再回答所提出的问题：
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x) =(1+x)3
(1)上述分解因式的方法是 ，共应用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004，则需应用上述方法 次，
结果是 .
(3)分解因式：1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).
19． 如图，直线AC∥DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。以下是他的想法，请你填上根据。
小华是这样想的：
因为CF和BE相交于点O，
根据 得出∠COB＝∠EOF；
而O是CF的中点，那么CO＝FO，又已知 EO＝BO，
根据 得出⊿COB≌⊿FOE， （第19题图）
根据 得出BC＝EF，
根据 得出∠BCO＝∠F，
既然∠BCO＝∠F，根据 出AB∥DF，
既然AB∥DF，根据 得出∠ACE和∠DEC互补。
20．要在已知袋子中装入若干个形状、大小完全相同的小球，使得从袋子中任意摸出一个红球的概率为
，请你给出一种放球的方法。
21．如图，直线a是一个轴对称图形的对称轴，画出这个轴对称图形的另一半，并说明这个轴对称图形是一个什么图形，它一共有几条对称轴。
 |
（第21题图）
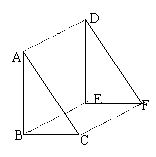
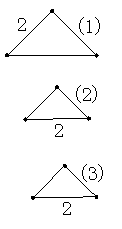
22.如图:有三块等腰直角三角形的纸板,其中(1)的直角边长为2,(2)、(3)的斜边长为2,请利用这三块纸板拼成形状不同的四边形，并画在下列空白处.
 |
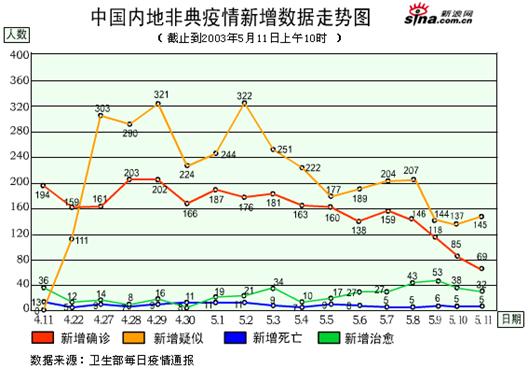
23．据新浪网消息，下图为“中国内地非典疫情新增数据走势图”（截止到2003年5月10上午10时），回答下列问题：
（1）什么时间新增确诊人数最多，最多是多少？
（2）什么时间范围内，新增确诊人数开始逐步下降？
（3）通过以上数据和走势图，对在我国这一次发生的“非典”疫情，进行简要的评述，并对今 后疫情的走势进行预测．
 |
25．下表是我国的几个省（自治区）的年降水量以及纬度位置。
| 省（自治区） | 广东省 | 湖北 | 河南 | 内蒙古 自治区 |
| 纬度位置 （北 纬） | 3度至25度 | 29度至33度 | 31度至36度 | 38度至53度 |
| 年降水量 | 1800毫米 | 1200毫米 | 900毫米 | 300毫米 |
(1)表中的数字都是近似数，其中四个年降水量都是精确到100毫米得到的，那么广东省的年降水量1800毫米这个近似数有 个有效数字。
(2)从表中可以看出，这四个省（自治区）年降水量随着纬度位置的变化而变化，这样请你说出在这个问题中，什么是自变量？什么是因变量？并说一说降水量是怎样随着纬度位置的变化而变化的？
26．老师要小华用一张纸片制作成一个如图②的形状的图案，他是这样做的：先画一条线段AC（如图①），再以AC为直径画圆（O是它的圆心），并剪下这个圆，然后在AC上找一点B，再分别以AB、BC为直径画圆，然后用剪子或其它工具挖去这两个圆（即以O1、O2为圆心的圆），再通过适当的剪裁，就可以得到图②。如果被挖去两个圆中，小圆的半径（即AO2）比大圆的半径（即CO1）小1cm，请你比较余下的部分的面积（即图①中阴影部分的面积）和被挖去的部分的面积（即两个小圆的面积的和）的大小。
（图①） （图②）
27．还记得我们上学期学过的七巧板吗？它是我们的祖先的一项卓越创造，它虽然只有七块，但是可以拼出多种多样的图形。如图就是一个七巧板，这七块刚好拼成一个四个角都是直角的正方形。上图中有三对全等的三角形，如：⊿ABN≌⊿ADN，也有几对全等的四边形。
（1） 请你根据全等图形的特征，求出∠BAN的度数；
（2） 请你写出一对全等的四边形和另外两对全等的三角形（请把表示对应的顶点的字母写在对应的位置）。
 |
（第27题图）
28. 某城市出租车的起步价是10元(即行驶5千米以内都需付10元车费),达到或超过5千米后,每行驶1千米加收1.4元(不足1千米按1千米计算),现某人乘车从甲地到乙地,支付车费19.8元,问:从甲地到乙地的路程大约是多少?
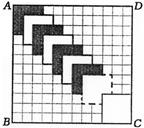
29.如图，正方形ABCD的边长为12，划分成12×12个小正方形格. 将边长为n（n为整数，
且2≤n≤11）的黑白两色正方形纸片按图中的方式黑白相间地摆放，第一张n×n的纸片
正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为（n－1）×（n－1）的正方形. 如此摆放下去，最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题：
(1) 由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 |
(2)设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S1，未被盖住的面积为S2.
①当n=2时，求S1∶S2的值；
②是否存在使得S1=S2的n值，若存在，请求出这样的n值；若不存在，请说明理由.
 |