初三上学期数学--解直角三角形单元检测题（B）
满分：100分；考试时间：90分钟
姓名： 学号： 成绩：
一、填空题：（每小题2分，共20分）
1、△ABC中，AB＝AC＝10cm，BC＝12cm，则cosB＝ ，cotB＝ 。
2、计算：cot440·cot450·cot460＝
；若
，00＜
＜900，则＝_______。
3、在Rt△ABC中，∠C＝900，如果已知
和∠B，则
＝ ，
＝
。（用锐角三角函数表示）
4、如果是锐角，且cos＝
，那么sin
＝ 。
5、在Rt△ABC中，∠C＝900，＝2，＝
，则tan
＝
。
6、计算：
＝
。
7、已知Rt△ABC中，∠C＝900，
，则∠B＝
。
8、计算sin30°＋9cos600＝___________；若
，则cos＝____________。
9、比较大小：sin520_________cos460
10、某人沿着山坡走到山顶共走了1000米，它上升的高度为500米，这个山坡的坡度为__________，坡角为__________。
二、选择题：（每小题2分，共20分）
11、下列各式中，正确的是（ ）
A、sin(300＋600)＝sin300＋sin600
B、cot400＝
C、
D、 tanA·sinA＝cosA
12、利用投影仪把Rt△ABC各边的长度都扩大5倍，则锐角A的各三角函数值（ ）
A、都扩大5倍 B、都缩小5倍 C、没有变化 D、不能确定
13、在Rt△ABC中，∠C＝900，sinA＝
，则tanB的值为（ ）
A、
B、
C、
D、
14、在Rt△ABC中，∠C＝900，cosA＝
，＝，则等于（
）
A、
B、1
C、2
D、3
15、已知tan600－cotA＝0，A是锐角，则sinA的值是（ ）
A、
B、
C、
D、
16、在Rt△ABC中，∠C＝900，下列关系式一定不成立的是（ ）
A、
B、
C、
D、
17、在Rt△ABC中，∠C＝900，、分别为∠A、∠B的对边，且满足
则tanA的值为（ ）
A、5或6 B、2 C、3 D、2或3
18、在△ABC中，∠A∶∠B∶∠C＝1∶2∶3，则
＝ ( )
A、 B、 1 C、
D、
19、已知A、B两点，若由A看B的仰角为，则由B看A的俯角为 ( )
A、
B、
C、
D、 
20、等腰三角形的顶角A＝1200，底边BC的长为12cm ,那么它的腰长是 ( )
A、
cm B、
cm C、cm
D、6cm
三、计算下列各题：（每小题5分，共10分）
21、
22、
四、解答下列各题：（每小题8分，共40分）
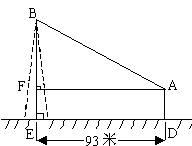
23、如图，在离铁塔93米的A处，用测角器测得塔顶的仰角为∠BAF，已知测角器高AD＝1.55米，若∠BAF＝30°，求铁塔高BE。
解：
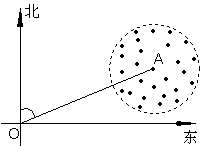
24、如图，灯塔A周围1000米水域内有礁石，一舰艇由西向东航行，在O处测得灯塔A在北偏东740方向上，这时O、A相距4200米，如果不改变航向，继续向东航行，此舰艇是否有触礁的危险？（以下数据供考生选用：cos740＝0.2756，sin740＝0.9613，cot740＝0.2867，tan740＝3.487）
25、已知A、B、C是△ABC的三个内角，求证：
＝
26、如图，海上有一灯塔P，在它周围4千米内有暗礁，一艘轮船以每小时9千米的速度由东向西行驶，行至A处测得灯塔P在它的北偏西75°，继续行驶一小时到达B处，又测得灯塔P在它的北偏西60°，试问：若客轮不改变航向，是否有触礁的危险？（供考生参考的数据：tan150≈0.2679，cot150≈3.732，≈1.732）
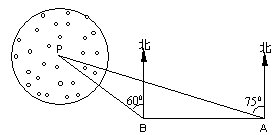
27、在Rt△ABC中，∠C＝90º，、、分别为∠A、∠B、∠C的对边，tanA、tanB是关于
的一元二次方程
的两个实数根。①求
的值。 ②若＝10且＞,求、的长。
五、知识运用：（10分）
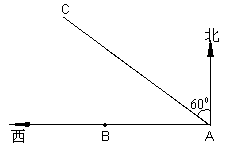
28、如图，某货船以20海里／时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，到达后必须立即卸货．此时，接到气象部门通知，一台风中心正以40海里／时的速度由A向北偏西600方向移动。距台风中心200海里的圆形区域（包括边界）均会受到影响。
（1）问：B处是否会受到台风的影响？请说明理由。
（2）为避免受到台风的影响，该船应在多少小时内卸完货物？
（供选用的数据：
≈1.4，≈1.7）
参考答案
一、填空题：
1、
，
；2、1，600；3、
，
；4、；5、；6、1；7、600；
8、5，；9、＞；10、1∶，300
二、选择题：CCABB，DDCCB
三、计算下列各题：
21、
22、
四、解答下列各题：
23、解：在Rt△ABF中，∵tan∠BAF＝
∴BF＝AF·tan∠BAF＝93×tan300＝93×＝
(米)
∴BE＝BF＋FE＝BF＋AD＝
(米)
答：铁塔高BE约为55.24米。
24、解：过A作AB⊥OB于B，由题意知：∠AOB＝900－740，AO＝4200米
∵
∴AB＝
＝
＝
≈
≈1157.52（米）
∵AB＞1000
∴不改变航向，继续向东航行，此舰艇不会有触礁危险。
25、证明：∵A＋B＋C＝1800
∴A＝1800－（B＋C）
∴
∴
∴
26、解：过P作PC⊥AB的延长线于C，由题意知：AB＝9，∠PAC＝150，∠PBC＝300
∵AC＝
BC＝
∴AC－BC＝
即
∴PC≈4.5＞4
∴客轮不改变航向，继续向西前行，不会有触礁危险。
27、解：①由韦达定理得：
即
∴
∴
此时一元二次方程可化为；
由△≥0得：≥
或≤－
∵不符题意，应舍去。
∴的值为
。
②原方程可化为：
又∵＞
∴
设＝
，那么＝
由勾股定理得：
即
解得：＝
∴＝
＝
＝
＝
28、
解：（1）过B作BD⊥AC于D，由题意知：∠BAC＝300，AB＝16×20＝320（海里）
∵
∴BD＝
＝
＝160（海里）
∵BD＜200
∴B处会受到台风的影响。
（2）以点B为圆心，200海里为半径画圆交AC于E、F，则BE＝200海里
在Rt△BED中，由勾股定理得：
即
∴DE＝120
又∵AD＝
（海里）
AE＝AD－DE＝
（海里）
∴
（小时）
∴为避免受到台风的影响，该船应在3.8小时内卸完货物。