初三升学模拟考数学试题卷
考生须知：
1、本试卷分试题卷和答题卷两部分，满分120分，考试时间100分钟。
2、必须在答题卷的对应答题位置答题。
3、答题前，应先在答题卷上填写班级、姓名、学号。
一、选择题（本题有15个小题，每小题3分，共45分）
1．冬季某天我国三个城市的最高气温分别是－10℃、1℃、－7℃，把它们从高到低排列正确的是
A、－10℃、－7℃、1℃ B、－7℃、－10℃、1℃
C、1℃、－7℃、－10℃ D、1℃ 、－10℃、－7℃
2．手电筒发射出的光线，给我们的形象似
A、线段 B、射线 C、直线 D、折线
3、二次函数
的最小值是
A、4 B、2 C、3 D、－1
4．某省有7万名学生参加初中毕业考试，要想了解这7万名学生的数学成绩，从中抽取了1000名考生的数学成绩进行统计分析，以下说法正确的是
A、这1000名考生是总体的一个样本 B、每位考生的数学成绩是个体
C、7万名考生是总体 D、1000名考生是样本容量
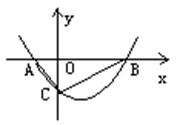
5．葡萄熟了，从葡萄架上落下来，下图的图象可大致反映葡萄下落过程中的速度v随时间t变化情况的是
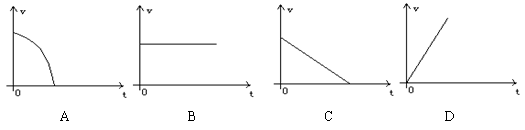
6．已知x为实数，设M=
，N=
，则M、N的大小关系为
A、
B、
C、
D、以上都不对
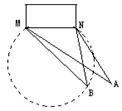
7．在足球比赛场上，甲、乙两名队员相互配合向对方球门MN进攻。当
甲带球冲到点A时，乙已跟随冲到点B，如图。从数学的角度看，
此时是甲自己射门好，还是将球传给乙，让乙射门好？
A、甲好 B、乙好 C、一样 D、不能确定
数学试题卷—1（共4页）
8．如果方程组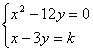
有两组相同的解，则k的值是
|
|
A、1 B、－1 C、±1 D、0
|
|
|
|
A、
B、
C、
D、
10．在实数范围内分解因式－2x2 + 3x + 1的结果是
A、(x－)(x－) B、－2(x－)(x－)
C、(x+)(x+) D、－2(x+)(x+)
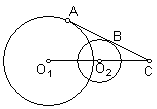11．如图，半径为R和r ( R > r )的两圆O1与O2相交，公切线与连心线的夹角为30°，两圆公切线的长AB =
A、
B、
C、
D、
12．某件商品的标价为13200元，若降价以9折出售，仍可获利10%（相对进货价），则该商品的进货价是A、10800元 B、105600元 C、10692元 D、11880元
13．若顺次连接四边形各边中点得到一个正方形，则原四边形满足
A、两条对角线相等但不互相垂直 B、两条对角线互相垂直但不相等
C、两条对角线互相平分但不相等 D、两条对角线相等且互相垂直
14．已知，△ABC中，∠BAC=100°，AB=4，AC=3，则△ABC的面积为
A、6sin80° B、12sin80°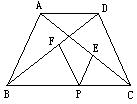
C、6cos100° D、12cos100°
15．如图，在梯形ABCD中，AD//BC，AB=DC=3，P是BC上一动点，
PE//AB交AC于E，PF//CD交BD于F；设PE、PF的长分别为m、
n，且x = m + n，那么点P在BC上移动时，x的值
A、大于3 B、等于3 C、小于3 D、等于4
数学试题卷—2（共4页）
二、填空题（本题有5个小题，每小题4分，共20分）
16．在我国南宋大数学家秦九韶（1202~1261）的著作中，出现了十进小数的记法，例如，他把324506.25记为如图a的形式，用“馀”字表明该位以后都是小数部分，“馀”就是现在的小数点。
（1）请把123.46表示为图a的形式。
（2）图b表示的数为 。
|
红色地毯，已知这种地毯每平方米售价30元，主楼梯道宽
2米，其侧面如图所示，则购买地毯至少需要
元。
|
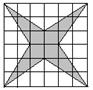块6cm×6cm的印有方格的布上用丝线绣的。则当小猫去抓这
个饰物时，抓到丝线的可能性为 。
19．先阅读，然后回答问题：
式子“1+2+3+4+……+100”表示从1开始的100个连续的自然
数的和。由于上述式子比较长，书写也不方便，为了简便起见，
我们可以将“1+2+3+4+……+100”表示为
，这里“
”是求和符号。
例如：“1+3+5+7+……+99”可表示为
；
又如：
=
；
请计算：
=
。
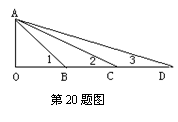
20．如图，∠AOD=90°，AO=BO=BC=CD，则在（1）∠1+∠2+∠3=90° ，（2）∠BAC=∠BDA，（3）△BAC∽△BDA，（4）中，正确结论的序号是 （把你认为正确的都填上）。
三、解答题（本题有6个小题，共55分）
21．（1）计算：
（2）解不等式组：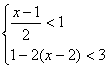
22．阅读下面的材料，然后解答问题：
已知：x > 0，符号[x]表示大于或等于x的最小整数，如[2.3]=3，[5]=5，……
（1）填空：
= ，
= ；若
，则x的取值范围是 。
数学试题卷—3（共4页）
（2）某市的出租车收费标准如下：5km以上（含5km）收费6元，超过5km时，每超过1km收费1.2元（不足1km按1km计算），用x表示所行路程（单位：km），y表示行xkm应付车费，则乘车费可按如下公式计算：
某乘客乘车21.6元，求该乘客所行的路程x(km)的取值范围。
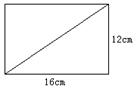
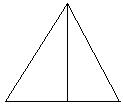
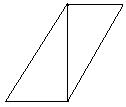
23．用硬纸板剪一个长为16cm、宽为12cm的长方形，再沿对角线把
它分成两个三角形（如图），请你画出用这两个三角形拼出各种三角形和四边形（不能重叠），计算出每一个的周长，并指出它们当中哪一个周长最大，哪一个周长最小？
| 景点 | A | B | C | D | E |
| 原价（元） | 10 | 10 | 15 | 20 | 25 |
| 现价（元） | 5 | 5 | 15 | 25 | 30 |
| 平均日人数（千人） | 1 | 1 | 2 | 3 | 2 |
24．某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变，有关数据如下表所示：
（1）该风景区称调整前后这5个景点门票的平均收费不变，平均日总收入持平。 问风景区是这样计算的？
（2）另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，实际上增加了约9.4%。问游客是怎样计算的？
（3）你认为风景区和游客哪一个的说法较能反映整体实际？
25．如图：抛物线
与x轴交于A、B两点，交
y轴负半轴与C点，∠ACB=90°，且
，
求△ABC外接圆的面积。
26．2001年4月13日，江泽民主席在古巴访问时，曾向卡斯特罗主席赠送了他亲笔书写的七绝一首。现借用江主席这首诗中的28个字编一个地名谜：
先将这首诗编号如下：
朝 辞 华 夏 彩 云 间，万 里 南 美 十 日 还；
1 2 3 4 5 6 7 8 9 10 11 12 13 14
隔 岸 风 声 狂 带 雨，青 松 傲 骨 定 如 山。
15 16 17 18 19 20 21 22 23 24 25 26 27 28
请你从中选出两个字组成一地名，但需满足下列条件：
（1）第一个字编号数为
之值；
（2）第二个字编号为一个四边形的周长，已知这个四边形，其中每三边的和分别为22、20、17、25；
你能说出这个地名吗？试说明理由。
数学试题卷—4（共4页）
升学模拟考数学参考答案
一、选择题（每小题3分，共45分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 | C | B | B | B | D | A | B | A | D | B | C | A | D | A | B |
二、填空题（每小题4分，共20分）
16． 134506.3 17． 504
18． 
19．
54
20、
（1）（2）（3）（4）
三、解答题（本题有6小题，共55分）
21、（1）3分，（2）4分
解：（1）原式=
–2 –
=
解：（2）由①得：x < 3 ;
由②得：x > 1
∴原不等式组的解集为1 < x < 3
22、（本题8分）
解：（1）填空：= 1 ，= 6 ；
若，则x的取值范围是 
。
（2）把
代入
，得
∴
，即
23、（本题8分）
 |
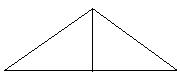P=64cm P=72cm P=72cm
 | |||||
 | |||||
 | |||||
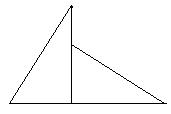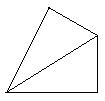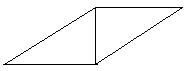p=64cm P=72cm P=56cm
数学答案1
24、（本题10分）
解：（1）风景区是这样算的：
调整前的平均价格=
调整后的平均价格=
因为调整前后的平均价格不变，平均人数不变，所以平均日总收入不变。
（2）游客是这样计算的：
原平均日总收入=10
1+101+152+203+252=160（千元）
现平均日总收入=51+51+215+253+302=175（千元）
所以，平均日总收入增加了，增加的百分率=
（3）游客的说法能反映整体实际。
25、（本题10分）
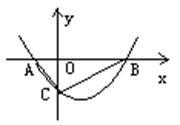解：设A（x1,0）、B（x2,0），易知C（0，q）；
∵
，由射影定理得OC2=OA•OB，
∴
=
解得
，（
舍去）
又由得：
，
∴
，
，∴p=-2
故原抛物线的解析式为
，
Rt△ABC的斜边AB 的长=
=
，它的外接圆直径也为，
∴△ABC的外接圆面积为2
26、（本题12分）
解：（1）=
=3
（2）设此四边形的周长为x，则这个四边形的四条边的长分别为
,
,
,
;
∴（）+（）+（）+（） = x ，解得x =28
故所求地名为“华山”
数学答案2