初三数学（总）综合训练题12（两圆关系）
班级_________姓名__________ 得分__________
一、填空题
1．两圆有三条公切线，那么这两圆的位置关系是 ；
2．若两圆外切，圆心距为16 cm，且两圆的半径之比为5：3，则大圆的半径为 ，
小圆的半径为 ；
3.已知P为边长是2的正六边形ABCDEF内一点，P点到各边的距离分别为h1、h2、h3 h4、h5、h6，则h1＋h2＋h3+h4＋h5＋h6＝
4．两圆圆心距
，两圆半径的长分别是方程
的两个根，则这两圆的位置关系是
；
5．已知两圆的半径
（
）是方程
的两个根，两圆的圆心距为
，
若
，则两圆的公切线有
条；
二、选择题
6．两圆相切，则公切线的条数为-------------------------------- -（ ）
A 、1 条； B、 2 条 ； C、 3 条 ； D 、1条或3条；
7．若两圆的半径分别为R、
（），圆心距为，且
，则两圆的位置关系为------------------------------------- -（ ）
A、不内含； B、不相切； C、相交； D、不相离；
8．两圆的半径分别是R、（
），圆心距为，且有等式
成立，则这两圆的位置关系是-------------------------------------- -（ ）
A、相交； B、外切； C、 内切； D 、外切或内切；
9、如图，以OB为直径的半圆与半圆O交于点P，A、O、C、B在同一条直线上，作
AD⊥ AB与BP的延长线交于点D，若半圆O的半径为2，∠D的余弦值是方程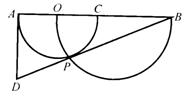
的根，则AB的长等于（ ）
（A）
（B）
（C）8（D）5
二、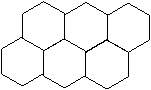
解答题
10． 我们常见到如下图那样的图案的地面，它们分别全用正方形或全用正六边形状的材料铺成，这样铺成平面平整，无空隙，为什么？现在问：象下面那样铺地面，能否全用正五边形材料，为什么？
11、如图，⊙O1经过⊙O的圆心，E、F是两圆的交点，直线OO1交⊙O于点Q、D，交
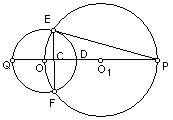⊙O1于点P，交EF于点C，且EF=
，sin∠P=
（1） 求证：PE是⊙O的切线；
（2） 求⊙O和⊙O1的半径的长；
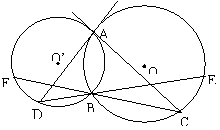12、已知：如图，⊙O和⊙O’相交于A、B两点，AC是⊙O’的切线，交⊙O于C点，连结CB并延长交⊙O’于点F，D为⊙O’上一点，且∠DAB＝∠C，连结DB交延长交⊙O于点E。
①求证： FD∥CA;
②若BF＝4，CA＝
，求CB的长。 ；
13．已知：矩形ABCD中，CD=2，AD=3，P是AD上的一个动点，且和A、D不重合，过P作
PE⊥CP交直线AB于E，设PD=x， AE=y。写出y关于x的函数解析式，并写出x的取值范围。
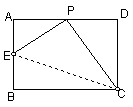
参考答案与提示：
1、外切
2、10，6；
3、6
；
4、外离；
5、4；
6、D；
7、A；
8、C；
9、C；
10、用正方形或全用正六边形状的材料铺成，这样铺成平面平整，无空隙，因为正六边形每个内角为1200，1200能被3600整除。 象下面那样铺地面，不能全用正五边形材料，因为正五边形每个内角为1080，1080不能被3600整除。
11、提示：（1）连OE，∠0EP=90O； （2）0E = 4，OO1 = 8；
12、提示：（1）连FD，AB，∠DFB=∠DAB=∠BCA； （2）5；
13、y=-x2 +x , xÎ(0 , );
]