中考数学模拟试卷（四）

中考数学模拟试卷（四）

一、填空题(每题4分，共20分)

1、用语言叙述代数式，正确的是(　 )

A、a、b两数的平方差；B、a与b的差的平方；

C、a与b的平方的差； D、b、a两数的平方差。

2、数据1、2、8、5、3、9、5、4、5、4的众数、中位数分别为(　 )

A、4.5、5；B、5、4.5；C、5、4；D、5、5。

3、已知两圆的半径满足方程，圆心距为1，则两圆的位置关系是(　 )

A、相交；B、外切；C、内切；D、外离。

4、如图，两枚同样大小的硬币，其中一个固定，另一个沿其周围滚动，滚动时，两枚硬币总是保持有一点相接触(相外切)，当滚动的硬币沿固定的硬币滚动一圈，回到原来的位置时，滚动的那一个硬币自转的周数为(　 )

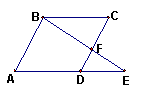
A、1；B、2；C、3；D、4。

5、已知等腰直角三角形外接圆半径为5，则内切圆半径为(　 )

A、；B、；

C、；D、。

二、填空题(每题3分，共24分)

6、若关于x的一元二次方程

有两个实数根，则k的取值范围是　　　　　  。

7、等边三角形外接圆面积是内切圆面积的

　　倍。

8、一条弦把圆分成2：3的两部分，那么这条弦所对的圆周角的度数为　　　　　 。

9、分解因式：

＝　　　　　　　　　　　  。

10、由矩形的一个顶点作对角线的垂线，垂足将这条对角线分成长度为3：1的两段，若矩形的一条边长为5cm，则对角线长为　　　　  cm。

11、已知扇形的圆心角为150⁰，弧长为20厘米，则这个扇形的半径为　　　　　  厘米。

12、已知，，且b<0，那么a：b＝　　　　。

13、如图，E是平行四边形ABCD的边AD延长线上一点，且D为AE的黄金分割点，即，BE交DC于点F，已知，则CF的长是　　　　　 。

三、解答题

14、(6分)解方程：

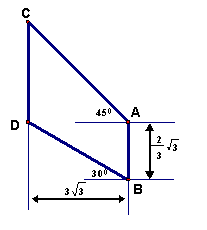
15、(10分)某型号的飞机机翼如图，其中AB∥CD，根据图中的数据计算AC、BD和CD的长度(结果保留根号)。

16、(10分)已知二次函数

的图象与x轴的交点为A、B（点B在点A的右边），与y轴的交点为C。(1)若△ABC为直角三角形，求m的值；(2)在△ABC中，若AC＝BC，求∠ACB的正弦值；(3)设△ABC的面积为S，求当m为何值时，S有最小值，并求这个最小值。

17、(10分)已知方程的两根平方和为1，其中∠A为锐角三角形的一个内角，(1)求sinA；(2)若△ABC的两边的长是方程组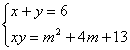 (m为实数)的解，求△ABC的第三边长和内切圆的半径。

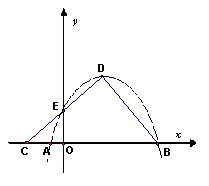18、(10分)如图，抛物线的顶点为D(不在y轴上)，交x轴于点A、B，交y轴于点E，直线DE交x轴于点C，∠ACD＝45⁰，

∠ABD＝60⁰，若AB＝，求：(1)S_△BCD；(2)抛物线的解析式。

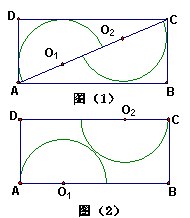
19、(10分)如图，矩形木板ABCD中，长AB＝a米，宽BC＝b米，要从矩形木板ABCD上截下两个相同的半圆面，拼成一个圆桌面，有如下两种截法：如图(1)点O₁、O₂在AC上，⊙O₁与⊙O₂分别与矩形ABCD两边相切；如图(2)点O₁、O₂分别在AB、CD上，⊙O₁与⊙O₂都相切，⊙O₁、⊙O₂分别与AD、BC相切。

(1)求图(1)中，半圆的半径R的长(用a、b的代数式表示)；

(2)求图(2)中，半圆的半径r的长(用a、b的代数式表示)；

(3)如果用长2米，宽1米的两块矩形木板各做一个圆桌面，每块木板都有上述两种截法，请问对这两块木板应当采用哪一种截法，做出的圆桌面较大。