中考数学实战冲刺之―

中考数学实战冲刺之―

　　一、考点：

　　近年中考考查实数（含有理数、无理数运算等）和代数式（含因式分解、分式运算、根式运算等）以及分式内容的题型较多，多以填空和选择题的形式出现，还有判断、比较大小、求绝对值以及求分式的值等题型也比较常见。重点考查：
　　①相反数、倒数、绝对值、平方根、算术平方根、有理数、无理数等概念的掌握情况。

　　②实数大小的比较、简单的实数运算等内容。

　　③把一个数科学记数，正确把握近似数的精确度和有效数字之间的关系。

　　④利用数轴，靠直观判断给出实数的特点，进行实数的化简与计算。

　　⑤掌握整式、分式、根式的运算。

　　⑥掌握因式分解的运算。

　　⑦能发现和总结一些规律。

　　二、难点提示：

　　1.求一个数的相反数：数a的相反数是-a，由此可得如下方法：

　　（1）求一个数的相反数，只要在这个数的前面添加一个“-”号；所得的数即是这个数的相反数。
　　注意：若a是正数，则-a是负数；若a是负数，则-a是正数，若a是０，则-a是０即-０=０。

　　（2）多重符号的化简：一个数的前面带“+”号，可去掉“+”号；一个数前面带有两个负号，可把两个负号同时去掉。遇到有两个以上符号的数，则需把符号化去，使之只带一个符号或不带符号。如:
–[–(–3)]=–[3]=–3。

　　2.有理数和无理数统称实数。

　　实数有以下两种分类方法：

　　①按属性分类：

　　

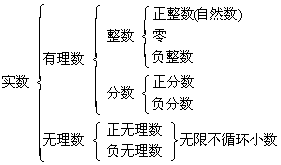
　　②按符号分类

　　

　　3.公式是字母表示数的一个重要应用，公式不是代数式，但公式的等号两边是代数式。有关公式的问题，一是用已学过的公式，如平面图形（三角形、长方形、正方形、平行四边形、梯形、圆等）的周长、面积公式和一些简单几何体（长方体、圆柱、圆锥等）的体积公式，还有一些数量关系公式如路程公式，浓度计算公式等，直接解决一些简单的实际问题。二是没有现成的公式，而需要从实际问题中总结出两个数量之间的对应数值关系，找出它们的联系规律，导出一般公式，再回到实际问题中解决问题。

　　4.利用提公因式法分解因式时，要防止出现以下错误：

　　①提不“全”或提不“净”现象：
　　如2a³–6a²–8a=a(2a²–6a–8)的错误原因是只注意到字母的指数，而没有提系数的最大公约数。

　　②出现“丢项”：
　　如4a²b²–6a²b+2a²=2a²(2b²–3b)的错误原因是丢项（2a²），当某一项恰是这个多项式各项的公因式时，它被提出后不是没有了，而是还有“1”。

　　③首项系数为负数的，应先提出负号，使括号内首项系数为正，同时，括号内各项都要变号。例如–a²+2ab–3ac=–a(a+2b–3c)的错误在提“–a”后括号内各项没有变号。

　　5.分式四则混合运算，是整式运算。因式分解和分式运算的综合运用。因此，很好地掌握多项式的因式分解及四则运算顺序是运算正确的保证。

　　6.根式的化简。

　　（1）利用积的算术平方根的性质，可将被开方数中的开方开得尽的因式，用它的算术平方根代替，而把它移到根号外，也可把根号外的非负因式平方后移到根号内。如：===2，3==。

　　一般地，如果a≥0，那么=a。这里同样要注意a≥0的条件，防止发生=–3的错误。

　　另外，一般地，如果a₁≥0，a₂≥0……a_n≥0，那么=·…。

　　（2）对式子的讨论，在化简时，要进行分类讨论。由于一个实数可能是正数、零和负数三种情形，所以上述式子实际表示三种情形：
　　当a>0时，=a=a；
　　当a=0时，=a=0；
　　当a<0时，=a=–a。

　　我们在计算的过程中，要牢记=a这一中间结果，然后再对不同符号的a值，脱去绝对值符号，这样可使运算少出差错。=a=

　　这个性质主要是强调当字母a可能取负数时，对二次根式的化简应注意符号。

　　7.二次根式的一个重要性质：()²=a(a≥0)，这个式子表明：一个非负实数的算术平方根的平方等于原来的非负数。而把这个式子反过来，还可得到：a=()²(a≥0)，这时式子表明：任何一个非负实数都可写成这个数的算术平方根的平方。

　　式子()²=a(a≥0)经常正向使用，也经常反向使用。在涉及到把一个二次根式平方时，正向使用公式得计算结果。如：。

　　三.注意事项:

　　（1）区别形如(-3)⁴与-3⁴的乘方运算的意义，前者表示(-3)×(-3)×(-3)×(-3)；后者表示
-(3×3×3×3)。前者表述为负3的四次方，后者表述为3的四次方的相反数，所以当底数是负数时，一定要添加括号。

　　（2）区别()⁴与的意义，前者表示×××，表述为的四次方；后者表示，表述为2的四次方与3的商，所以当底数是分数时，也要注意添加括号。

　　（3）因式分解的结果必须是几个整式的积的形式。
　　 　　如：4a²+6ab–8a=2a(2a+3b–4)是因式分解，但像
　　（1）a²–b²=(a+b)²·；（2）a²–2ab+3a=a(a–2b)+3a；都不是因式分解。因为（1）中不是整式；（2）中a(a–2b)+3a不是积的形式。

　　四、中考真题解析
　　1．（2001　 河北省）分母有理化:=_________。

　　考点：分母有理化。

　　评析：首先理解分母有理化的含义，然后找到分母–1的有理化因式+1，最后根据分数的性质，分子、分母同乘以因式（+1）就达到了分母有理化的目的，其结果为+1。

　　2.计算：()^–1–(2001+)⁰+(–2)²×⁺

　　考点：二次根式的除法，零指数幂，负整数指数幂

　　评析：该题是一综合运算试题，考查学生综合运算能力，只要学生对零指数幂a⁰=1（a≠0），负整数指数
幂a^–p=（a≠0），算术根及二次根式的除法掌握熟练，该题就能顺利的解答，具体过程为：
　　原式=3–1+4×+（+1）=4+

　　3.（2001年　 北京朝阳区）计算
　　解：–tg60^O–(–2001)⁰+()^–1
　　　 =
　　　 =
　　　 =2+–1+2
　　　 =3

　　4.（2001　 河南省）若=3，=2，a·b＜0，则a–b=　　　 。

　　考点：绝对值的意义、二次根式成立的条件

　　评析：由绝对值的意义可知a=±3，根据二次根式成立的条件被开方数大于等于0，所以b=4，又a·b＜0，因此a=–3。故a–b=–7。

　　5.（2001　 北京崇文区）计算+的结果正确的是（　 ）
　　A、　　　B、　　　C、1　　　D、3x

　　考点：分式的加法
　　评析：先通分，确定公分母为 (x+1)（x-1），然后再进行加减法运算，其结果为，故选A。

　　对于选择题，还可用“特殊值法”确定选项。方法是：给x以具体值（在允许范围内）分别计算各选项及原分式的值，看哪一选项与原分式的值相同，即为正确的选项。

　　解：令x=2，则原式=
　　A：　　　B：　　　C：1　　　D：3×2=6，因此应选A。

　　6.（2001　 黑龙江省哈尔滨市）先化简，再求值：，其中a=tg60°–1。

　　考点：分式的化简求值。

　　评析：此题是分式、三角函数、二次根式综合性试题。第一步先将分式通分，根据该题的特征易知公分母为(a+1) (a–1) , 然后再进行加减运算，最后化成最简分式，第二步将a值代入即可。解题过程如下：

　　解：原式＝

　　当a=tg60°-1＝时，

　　原式

　　说明：必须牢记特殊角的三角函数值，各知识点必须熟练，否则不能得满分。

　　7.（2002　 北京崇文区）因式分解：2x³－12x²y＋18xy²=__________________。

　　考点：提公因式法、公式法

　　评析：对于三项多项式的因式分解：一般运用公式法或形如x²＋(a＋b)x＋a·b=(x＋a)(x＋b)来分解。而该题提取公因式2x后将其提取后剩余部分为x²－6xy＋9y²=x²+(3y)²－2·x·(3y)，此三项多项式符合完全平方公式，所以原式分解为2x(x－3y)²。

　　8.（2001　 北京东城区）分解因式：2a³b+8a²b²+8ab³=_________________。

　　考点：提公因式法、公式法

　　评析：先提取公因式2ab，得到2ab(a²+4ab+4b²)，其中a²+4ab+4b²=a²+(2b)²+2a(2b)，符合完全平方公式，再继续分解，结果为2ab(a+2b)²。

　　说明：分解因式一定要彻底，中考一般考查两种方法的综合运用。

　　9.（2001　 云南昆明）x²–x+_________=(x–)²。

　　考点：公式法的灵活运用

　　评析：“配方”是完全平方公式的运用。由(x–)²=x²–x+可知应填。

　　10.（2002　 安徽省）已知x²–ax–24在整数范围内可以分解因式，则整数a的值是_________（只需填一个）

　　考点：公式x²+(a+b)x+ab=(x+a)(x+b)的灵活运用

　　评析：因为该题是在整数范围之内分解因式而24不是完全平方数，所以应该使用公式
x²+(a+b)x+ab=(x+a)(x+b) 。又因为－24可分解为(±24)×(1)或(±2)×(12)或(±3)×(8)或
(±4)×(6)。所以a的整数值有±23或±5或±10或±2。

　　11．（2001　 福建福州）观察下列各式：1²+1=1×2，2²+2=2×3, 3²+3=3×4，…… 　……
　　请你将猜想到的规律用自然数n(n≥1)表示出来　　　 。

　　考点：列代数式的运用

　　评析：该题是通过观察寻找规律，用代数式表示所得规律的问题，这是近年中考命题的热点问题，目的是考查学生观察分析及探究的能力。通过观察分析，该题的左边是一自然数的平方加上这个自然数，右边是这个自然数与下一个自然数的积，所以其规律用自然数n（n≥1）来表示应为：n²+n=n(n+1)

　　12.（2002　 北京西城区）-的倒数是（　 ）
　　A、　　　B、3　　　C、-　　　D、-3

　　考点：绝对值、倒数。

　　评析：根据绝对值的代数意义，可知-的绝对值是。再根据乘积是1的两个数互为倒数，所以的倒数是3，应选B。

　　13.（2001 江苏南京）在-2，3，4，-5这四个数中，任取两个数相乘，所得积最大的是（　 ）
　　A、20　　　B、-20　　　C、12　　　D、10

　　考点：有理数的乘法

　　评析：根据乘法法则两数相乘同号得正，异号得负及有理数大、小的比较法则。对于四个数-2，3，4，-5，两两相乘，得数分别为-6，-8，10，12，-15，-20。根据有理数大小的比较，在这六个数中只有12最大，所以应选C。

　　该题可拓展为三个数相乘，最大的积是　　　　 。或两两相乘所得积的最小值是　　　 。

　　14.（2001　 山西省）比较大小：-_________-(填“>”或“<”号)。

　　考点：两个负数大小的比较

　　评析：该题给出的是两个负分数，用数轴表示比较困难。而根据两个负数绝对值大的反而小的法则，易比较出它们的大小：具体过程是-==，-==，而＜，所以->-应填“>”号。

　　15.（2002　 北京西城区）观察下列各式：
　　　　×2=+2，×3=+3，×4=+4，×5=+5，……
　　想一想，什么样的两数之积等于这两数之和？设n表示正整数，用关于n的等式表示这个规律为：
　　　　　 ×　　　　　 =　　　　　 +　　　　　 。

　　考点：探究规律、导出公式。

　　评析：该题是通过观察给出的运算，找到反应其规律的表达式。这是中考中的一热点问题，此类问题不仅考查学生对知识的掌握，同时考查学生观察分析的能力。通过观察给出的四个等式左边是一个分数与一个整数的积且分数的分子比分母大1，而整数与分母相同。右边是这两个数的和，所以不难发现其规律为：左边，右边为

　　16.（北京海淀区）计算：(2-)²+(π-3.14)⁰-(2+)^-1。

　　解：(2-)²+(π-3.14)⁰-(2+)^-1=(4-4+3)+1-=8-4-(2-)=8-4-2+=6-3。

　　说明：在实数的混合运算中：（1）应先确定运算符号及顺序，再进行运算，有分数及小数时一般将小数化为分数较为简便；（2）熟悉运算律（包括正向与逆向）灵活运用各种运算法则，掌握一定的运算技巧；（3）注意零指数，负整数指数的定义（即：a⁰=1(a≠0)；a^-n=(a≠0)n为正整数）

　　17.（北京东城区）已知a=, b=, 求+2的值。

　　解： a==+2, b==-2, +2==。

　　当a=+2, b=-2时，原式==20。

　　说明：要注意两步的化简，一是给出字母的值，二是给出的代数式，另外，本题目还可以用整体代入的方法，先求出a+b=2,ab=1,整体直接代入化简后的代数式。

　　说明：分式运算要按运算顺序，进行计算和化简，分式乘除运算的关键是分子、分母的因式分解，因此，应随时注意分子、分母中多项式分解的可能性，以便进行约分，计算结果要化为分子、分母不要有公因式的最简形式。

　　实战练习:

　　一、选择题
　　1.（北京宣武区）在函数y=中，自变量x的取值范围是（　）
　　A、x>　　　B、x≥　　　C、x<　　　D、x≤

　　2.（北京崇文区）计算的结果正确的是（　）
　　A、　　　B、　　　C、　　　D、3x
　　3.（黑龙江）如果单项式-3x^4a-by²与x³y^a+b是同类项，那么这两个单项式的积是（　）
　　A、x⁶y⁴　　　B、-x³y²　　C、-x³y²　　　D、-x⁶y⁴

　　4.（武汉）化简的结果为（　）
　　A、-a　　　B、a　　　C、-a　　　D、a

　　5.（2002　 北京石景山）北京故宫的面积约为720000m²，用科学记数法表示为（　 ）
　　A、0.72×10⁶m²　　　B、7.2×10⁶m²　　　C、0.72×10⁵m²　　　D、7.2×10⁵m²

　　6.（2002　 北京崇文区）2001年北京市残联采取多种形式对45073名残疾人进行了不同类型的职业技能培训，数据45037保留2位有效数字，并用科学记数法表示为（　 ）
　　A、4.5×10³　　　B、4.5×10⁴　　　C、4.5×10⁵　　　D、45×10³

　　7.（2001　 宁波市）数a在数轴上的位置如图，则化简的结果是（　 ）
　　 　　　　
　　 A、–1　　　B、1–2a　　　C、1　　　D、2a–1

　　8.（2002　 北京朝阳区）化简的结果为（　 ）
　　 A、+1　　　B、–1　　　C、　　　D、

　　二、填空题

　　1.（武汉）分解因式：x²-bx-a²+ab=____________。

　　2.（天津）化简：=_________。

　　3.（北京东城区）若实数a、b满足3a-1+b²=0,则a^b的值为_________。

　　4.（吉林）今年3月，国家统计局公布我国总人口为129533万人。如果以亿为单位保留两位小数，可以写成约为_____________亿人。

　　5.（2002　 北京市燕山）分解因式：c²–a²–4b²+4ab=_________。

　　三、计算题
　　1.（辽宁）已知a=, b=，求a³b+ab³的值。

　　2.（济南）已知x=, 求·(1+)的值。

　　3．（武汉）=, 求÷(-x-2)的值。

　　四、（2001　 河南省）观察下列等式：
　　9-1=8，16-4=12，25-9=16，36-16=20，…， 这些等式反映出自然数间的某种规律，设n表示自然数，用关于n的等式表示出来：　　　 。

　　答案：

　　一、1、C　　2、A　　3、D　　4、C　　5、D　　6、B　　7、C　　8、D

　　二、1、（x-a）(x+a-b)　　2、2　　3、1　　4、12.95

　　5、解：c²–a²–4b²+4ab=c²–(a²–4ab+4b²)=c²–(a–2b)²=(c+a–2b)(c–a+2b)

　　三、1.解：∵a==-(+1), b==-1,
　　ab=-1, a+b=-2,
　　∴a³b+ab³=ab(a²+b²)=ab[(a+b)²-2ab]=(-1)×[(-2)²-2×(-1)]=-6。

　　

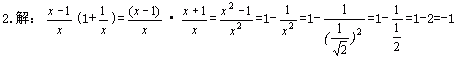
　　3. 解：原式=÷(-)=÷=·=-,
　　∵=, 即=+1，
　　∴1-=+1，　∴-=，
　　∴原式=-=。

　　四、答案：（n+2）²-n²=4(n+1)（提示：左边是两个自然数的平方差，其中前面的自然数比后面的自然数大2；右边是4的倍数。也可以按平方差公式展开右边结论）。