中考数学试卷2
一、选择题(本题12小题,每小题4分共48分)
1.-2的绝对值是( )A、1 B、-2 C、±2 D、2
2.下列图形中,不是轴对称图形的是( )
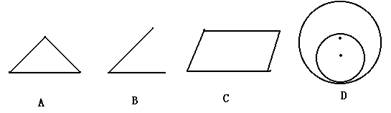
3.下列二次根式中,不是最简二次根式的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.在下列几何体中,轴截面是等腰梯形的是( )A、圆锥 B、圆台 C、圆柱 D、球
5.不等式3x-2≥0的解是( )A、x≥![]() B、x>
B、x>![]() C、x<
C、x<![]() D、x≤
D、x≤![]()
6.下列各个方程中,无解的方程是( )
A、![]() B、3(x-2)+1=0 C、x2-1=0 D、
B、3(x-2)+1=0 C、x2-1=0 D、![]()
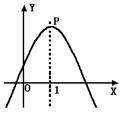 7.如图,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
7.如图,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
A、x>3 B、x<3 C、x>1 D、x<1
8.为了保障人民群众的身体健康,在预防“非典”期间,有关部门加强了对市场的监管力度。在对某商店检查中,抽检了5包口罩(每包10只),5包口罩中合格的口罩的只数分别是:9,10,9, 10,10,,则估计该商店出售的这仳口罩的合格率约为( )A、95% B、96% C、97% D、98%
9.已知直线l与⊙O相离,如果⊙O半径为R,O到直线l的距离为d,那么( )
A、d>R B、d<R C、d=R D、d≤R
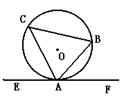 10.如果,⊙O是△ABC的外接圆,直线EF切⊙O于点A,若∠BAF=40°,则∠C等于( )
10.如果,⊙O是△ABC的外接圆,直线EF切⊙O于点A,若∠BAF=40°,则∠C等于( )
A、20° B、40° C、50° D、80°
11.方程x3-4x=0的解是( )
A、-2,2 B、0,-2 C、0,2 D、0,-2,2
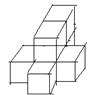 12.如果用□表示1个立方体,用
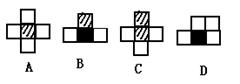
12.如果用□表示1个立方体,用![]() 表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
二;填空题(本题有6个小题,每小题5分共30分)
13.若无理数a满足不等式1<a<4,请写出两个你熟悉的无理数a: ; ;
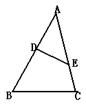 14.如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个条件,使△ABC与△AED相似。你添加的条件是:
;
14.如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个条件,使△ABC与△AED相似。你添加的条件是:
;
15.观察一列数:3,8,13,18,23,28……依次规律,在此数列中比2000大的数最小整数是 ;
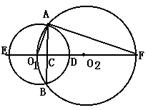 16.如图,⊙O1,⊙O2交于两点,点O1在⊙O2上,两圆的连心线交⊙O1于E,D,交⊙O2于F,交AB于点C。请你根据图中所给出的条件(不再标注其它字母,不再添加任何辅助线),写出两个线段之间的关系式:(1)
;(2)
;(半径相等除外)
16.如图,⊙O1,⊙O2交于两点,点O1在⊙O2上,两圆的连心线交⊙O1于E,D,交⊙O2于F,交AB于点C。请你根据图中所给出的条件(不再标注其它字母,不再添加任何辅助线),写出两个线段之间的关系式:(1)
;(2)
;(半径相等除外)
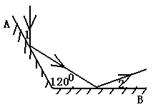 17.如图,平面镜A与B之间夹角为120°,光线经平面镜A反射在平面镜B上,再反射出去,若∠1=∠2,则∠1=
;
17.如图,平面镜A与B之间夹角为120°,光线经平面镜A反射在平面镜B上,再反射出去,若∠1=∠2,则∠1=
;
18.CD是Rt△ABC斜边止的高线,AD、BD是方程x2-6x+4=0的两根,则△ABC的面积为 ;
三、解答题
19.(本题8分)化简![]() +(
+(![]() -1)0-(
-1)0-(![]() )0;
)0;
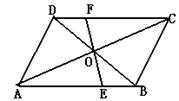 20.(本题9分)如图在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F。请你写出三对全等三角形:
;
; ;请你自选出其中的一对加以证明。
20.(本题9分)如图在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F。请你写出三对全等三角形:
;
; ;请你自选出其中的一对加以证明。
21.(本题8分)解方程组: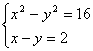
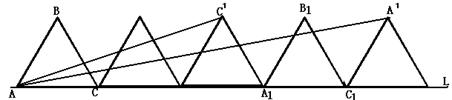
22.(本题9分)如图,已知边长为2的正三角形ABC沿着直线l滚动。(1)当△ABC滚动一周到△A1B1C1的位置,此时A点运动的路程为;约为;(精确到0.1,л=3.14…);(2)设△ABC滚动240°时,C点的位置为C’,△ABC滚动480°时,A点的位置为A’。请你利用三角函数中正切的两角和公式tan(α+β)=(tanα+ tanβ)÷(1-tanα·tanβ),求出∠CAC’+∠CAA’的度数。
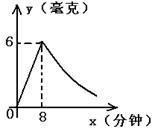 23.(本题12分)为了预防“非典“,某学校对教室采用药薰消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例,药物燃烧后,y与x成反比例(如图所示)。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克。请你根据题中所提供的信息,解答下列问题:(1)药物燃烧时y关于x的函数关系式为:
,自变量x的取值范围是:
;药物燃烧后y与x的函数关系式为:
;(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量低不低于1.6毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
23.(本题12分)为了预防“非典“,某学校对教室采用药薰消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例,药物燃烧后,y与x成反比例(如图所示)。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克。请你根据题中所提供的信息,解答下列问题:(1)药物燃烧时y关于x的函数关系式为:
,自变量x的取值范围是:
;药物燃烧后y与x的函数关系式为:
;(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量低不低于1.6毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
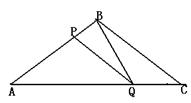 24.(本题12分)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x。(1)当x为何值时,PQ∥BC?(2)当
24.(本题12分)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x。(1)当x为何值时,PQ∥BC?(2)当![]() ,求
,求![]() 的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由。
的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由。
25.(本题14分)已知二次函数y=ax2+bx+c的图象与X轴交于A,B两点(A点在原点左侧,B点在原点右侧),与Y轴交于C点。若AB=4,OB>OA,且OA、OB是方程x2+kx+3=0的两根。(1)请求出A,B两点的坐标;(2)若点O到BC的距离为![]() ,求此二次函数的解析式;(3)若点P的横坐标为2,且ΔPAB的外心为M(1,1),试判断点P是否在(2)中所求的二次函数图象上。
,求此二次函数的解析式;(3)若点P的横坐标为2,且ΔPAB的外心为M(1,1),试判断点P是否在(2)中所求的二次函数图象上。