初高中衔接型中考数学试题（11）及参考答案

初高中衔接型中考数学试题（11）及参考答案

一、选择题

1．（浙江富阳2004）数轴上有两点A、B分别表示实数、，则线段AB的长度是（　　）

　　A、　　　　　B、　　　　C、　　　　D、

2．（浙江富阳2004）二次函数的图象与轴交点的个数是（　　）

A、0个　　　　B、1个　　　　C、2个　　　　D、不能确定

3．某种细菌在营养过程中，细菌每半小时分裂一次（由一个分裂为两个），经过两小时，这种细菌由1个可分裂繁殖成（　　）．

（A）8个　 （B）16个　 （C）4个　（D）32个

二、填空题

4．（浙江宁波2004）等腰三角形中，，、的长是关于的方程的两根，则的值是___________．

5．（浙江富阳2004）方程的解是　　　　　　　　　　　　；

三、解答题

6．（资阳市2004）已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立，求A、B的值.

7．（浙江富阳2004）已知一个长方体的木箱高为80，底面的长比宽多10，（1）求这个长方体的体积（）与长方体的宽（）之间的函数关系式；（2）问当该木箱的体积为0.72时，木箱底面的长与宽各为多少？

8． （河北省2001）某化工材料经销公司购进了一种化工原料共7000知克，购进价格为每千克30．物价部门规定其销售单价不得高于每千克70元，也不得低于30元．市场调查发现：单价定为70元时，日均销售60千克；单价每降低1元，日均多售出2千克．在销售过程中，每天还要支出其他费用500元（天数不足一天时，按整天计算）．设销售单价为x元，日均获利为y元．

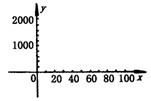
第8题图

　　（1）求y关于x的二次函数关系式，并注明x的取值范围；

　　（2）将（1）中所求出的二次函数配方成y＝a（x＋）² ＋　的形式，写出顶点坐标；在图9所示的坐标系中画出草图；观察图像，指出单价定为多少元时日均获利最多，是多少？

　　（3）若将这种化工原料全部售出，比较日均获利最多和销售单价最高这两种销售方式，哪一种获总利较多，多多少？

9．（北京西城2001）已知：Rt△ABC中，∠C＝90°．

（1）若AB＝c，∠A＝θ，用c和θ表示BC、AC；

（2）若AB＝5，sinA＝，P是AB边上一动点（不与点A、B重合），过点PA分别作PM⊥AC于点M，PN⊥BC于点N．设△AMP的面积为S、△PNB的面积为S、四边形CMPN的面积为S、AP＝x．分别求出S、S、S关于x的函数解析式；

（3）试比较S＋S与S的大小，并说明理由．

初高中衔接型中考数学试题（11）参考答案

一、

1、 答：C

2、　 答：C　

3、　  答：B

二、

4、　 答：25或16

5、　 答：　

三、

6、解：由题意有

(正确建立关于A、B的一个方程，给1分.)

解得：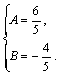

即A、B的值分别为、 .

7、解：（1）因为木箱的长、宽、高分别为：、、80　……2分

　　所以　　…………………………………………4分

（2）因为　0.72＝720000

所以　　　即　　……6分

解得：（舍去）　…………………………………7分

　　　

所以当木箱体积为0.72时，底面的长和宽分别为100和90。………8分

8、解：（1）若销售单价为x元，则每千克降低（70－x）元，日均多售出2（70－x）千克，日均销售量为［60＋2（70－x）］千克，每千克获得为（x－30）元．

　　依题意得：y＝（x－30）［60＋2（70－x）］－500＝－2 x²＋260 x－6500（30≤x≤70）．

　　（2）y＝－2 （x²－130 x）－6500＝－2（x－65）＋1950．顶点坐标为（65，1950）．

　　经观察可知，当单价定为65元时，日均获利最多，是1950元．

　　（3）当日均获利最多时：

　　单价为65元，日均销售60＋2（70－65）＝70千克，那么获总利为1950×＝195000元．

　　当销售单价最高时单价为70元，日均销售60千克，将这种化工原料全部售完需≈117天，那么获总利为（70－30）×7000－117×500＝221500元．

　　因为221500＞19500，且221500－19500＝26500元，所以，销售单价最高时获总利较多，且多获利26500元．

　　

9、解：

（1）

在Rt△ABC中，∠C＝90°，AB＝c，∠A＝θ，如图[第9题（1）]．

（以下这种表示必须熟记，今后经常用到．）

∵ sinA＝，∴ BC＝Ab sinA＝c sinθ．

∵ cosA＝，∴ AC＝Ab cosA＝c cosθ．

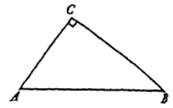
[第9题（1）]

（2）如图[第9题（2）]，过点P分别作PM⊥AC于点M，PN⊥BC于点N，则四边形CMPN是矩形．

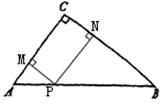
[第9题（2）]

∵ sinA＝，由锐角三角函数定义，

∴ cosA＝．

在Rt△APM中，∵ AP＝x，0＜x＜5，

又∵ PM＝Ap sinA＝x，AM＝Ap cosA＝x，

∴ ．

在Rt△PBN中，∵ PB＝AB－AP＝5－x，0＜x＜5，

同理可得

在矩形CMPN中，

∵ PM ＝x，PN＝（5－x），0＜x＜5， （注意解题过程中的每一步是怎样用已知条件的！）

∴

（3）

解法一：

∵

＝

＝　 　　　 （先明白这种解法的意义，再学会如何讨论．）

＝

∴ 当，即P为AB中点时，，此时．

当或，即P不为AB中点时，，此时．

解法二：

＝

＝

∵ 当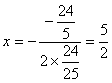时，的最小值为0，

∴ 当，即P为AB中点时，

当或，即P不为AB中点时，．

解法三：

当P为AB中点时，如图[第9题（3）]，连结PC．

∵ ∠ACB＝90°，∴ AP＝CP＝BP．　　 （这种方法“巧”在何处？）

不难推出：

△APM≌△CPM，△BPN≌△CPN．

∴

当P在AB中点左侧时，如图[第9题（4）]，作∠EPM＝∠APM，分别交MC于点F，交BC延长线于点E．

不难推出：

　　　　

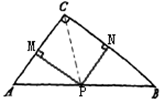
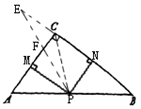
[第七题（3）]　　　　　　  [第七题（4）]

△FPM≌△APM，△EPN≌△BPN．

∵

∴

当P在AB中点右侧时，同理可证