初中毕业、升学统一考试数学试卷
（时间：120分钟，总分：150分）
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 合计 | 初积分人 | 复积分人 |
| 得分 |
第一部分 选择题（48分）
一、选择题：（每题只有一个正确答案，每题4分，计48分）
1. 
的倒数是
A． 
B．
C．
D．
2. 下列运算正确的是
A．(a＋b)2＝a2＋b2； B．(a－b)2＝a2－b2；
C．(a＋m)(b＋n)＝ab＋mn； D．(m＋n)(－m＋n)＝－m2＋n2
3. 2003年10月15日9时10分，我国“神州”五号载人飞船准确进入预定轨道，16日5时59分，返回舱与推进艇分离，返回地面。其间飞船绕地球共飞行了14圈，飞行的路程约60万千米，则“神州”五号飞船绕地球平均每圈约飞行（用科学计数法表示，结果保留三个有效数字）
A．4.28×104千米 B．4.29×104千米
C．4.28×105千米 D．4.29×105千米
4. △ABC中，AB＝３，BC＝４，则AC边的长满足
A．AC＝5 B．AC>1 C．AC<7 D．1<AC<7
5. 下列由正三角形和正方形拼成的图形中是轴对称图形而不是中心对称图形的是
 | |||||||
 | |||||||
 |  | ||||||
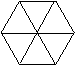A． B． C． D．
6. 圆内接四边形ABCD中，若∠A∶∠B∶∠C＝1∶2∶5，则∠D等于
A．60° B．120° C．140° D．150°
7. 已知⊙O1和⊙O2的半径分别为2和5，O1O2＝７，则⊙O1和⊙O2的位置关系是
A．外切 B．内切 C．相交 D．相离
8. 小芳和爸爸、妈妈三人玩跷跷板，三人的体重一共为150千克，爸爸坐在跷跷板的一端，体重只有妈妈一半的小芳和妈妈一同坐在跷跷板的另一端，这时，爸爸的那一端仍然着地。请你猜一猜小芳的体重应小于
A．49千克 B．50千克 C．24千克 D．25千克
9. 若代数式
的值是常数2，则a的取值范围是
A．a≥4 B．a≤2 C．2≤a≤4 D．a＝2或a＝4
10. 四边形ABCD中，AB∥CD，且AB、CD是关于x的方程x2－3mx＋2m2＋m－2＝0的两个实数根，则四边形ABCD是
A．矩形 B．平行四边形 C．梯形 D．平行四边形或梯形
11. 
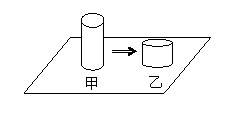用某种金属材料制成的高度为h的圆柱形物体甲如右图放在桌面上，它对桌面的压强为1000帕，将物体甲锻造成高度为
h的圆柱形物体乙（重量保持不变），则乙物体对桌面的压强为
A．500帕 B．1000帕
C．2000帕 D．250帕
12. 给出下列四个命题：
(1) 如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形；
(2) 若点A在直线y＝2x－3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；
(3) 半径为5的圆中，弦AB＝8，则圆周上到直线AB的距离为2的点共有四个；
(4)
若A（a，m）、B（a－1，n）（a>0）在反比例函数
的图象上，则m<n．
其中，正确命题的个数是
A．1个 B．2个 C．3个 D．4个
第二部分 非选择题（102分）
| 阅卷人 |
二、填空题：（每题3分，计28分）
13.
下列各数：
、π、
、
、sin60°中，无理数共有________个。
14.
函数
的自变量x的取值范围是______________。
15. 某工人师傅需要把一个半径是6cm的圆形铁片加工截出边长最大的正六边形铁片，则此正六边形的边长为__________cm。
16. 已知：如右图，△ABC中，BD平分∠ABC，且D为AC的中点，DE∥BC交AB于E，若BC＝4，则EB长为___________。
17. 泰州地区六月份某一周每天最高气温如下表：
| 星 期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 最高气温（℃） | 27 | 28 | 28 | 25 | 26 | 27 | 27 |
则这一周的最高气温的中位数是__________℃。
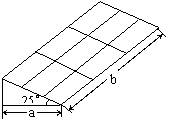
18. 李小同叔叔下岗后想自主创业搞大棚蔬菜种植，需要修一个如右图的育苗棚，棚宽a＝3米，棚顶与地面所成的角约为25°，长b＝9米，则覆盖在顶上的塑料膜至少需要______米2。（利用计算器计算，结果精确到1米2）
19. 为了能有效的使用电力资源，我市供电部门最近进行居民峰谷用电试点，每天8∶00至21∶00用电每千瓦时0.55元（“峰电”价），21∶00至次日8∶00每千瓦时0.30元（“谷电”价）。王老师家使用“峰谷”电后，五月份用电量为300千瓦时，付电费115元。则王老师家该月使用“峰电”_____________千瓦时。
20.
在距离地面2米高的某处把一物体以初速度v0（米/秒）竖直向上抛出，在不计空气阻力的情况下，其上升高度s（米）与抛出时间t（秒）满足：
（其中g是常数，通常取10米/秒2）。若v0＝10米/秒，则该物体在运动过程中最高点距地面________米。
| 阅卷人 |
三、解答题：（21、22每题6分，23、24每题7分，计26分）
21.
计算：
22.
化简：
23.
解方程：
24. 已知：如图，点D、E在△ABC的边BC上，AD＝AE，BD＝EC，
求证：AB＝AC
| 阅卷人 |
四、（本题9分）
25.
观察图1至图5中小黑点的摆放规律，并按照这样的规律继续摆放，记第n个图中小黑点的个数为y。
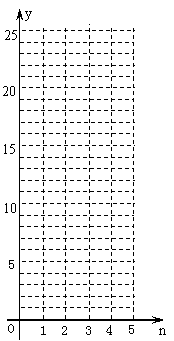图1 图2 图3 图4 图5
解答下列问题：
⑴ 填表：
| n | 1 | 2 | 3 | 4 | 5 | … |
| y | 1 | 3 | 7 | 13 | … |
⑵ 当n＝8时，y＝__________.
⑶ 根据上表中的数据，把n作为横坐标，把y作为纵坐标，在左图的平面直角坐标系中描出相应的各点（n,y），其中1≤n≤5.
⑷ 请你猜一猜上述各点会在某一函数的图象上吗？如果在某一函数的图象上，请写出该函数的解析式.
| 阅卷人 |
五、（本题9分）
26. 用剪刀将形状如图1所示的矩形纸片ABCD剪成两部分，其中M为AD的中点，用这两部分可以拼成一些新图形，如图2中的Rt△BCE就是拼成的一个图形。
 | |||||||
 | |||||||
 | |||||||
 | |||||||
（图1） （图2） （图3） （图4）
⑴ 用这两部分纸片除了可以拼成图2中的Rt△BCE外，还可以拼成一些四边形，请你试一试，把拼成的四边形分别画在图3、图4的虚框内。
⑵ 若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形，设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米，且a、b恰好是关于x的方程x2－(m－1)x＋m＋1＝0的两个实数根，试求出原矩形纸片的面积。
| 阅卷人 |
六、（本题10分）
27. “五一黄金周”的某一天，小明全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩。该小汽车离家的距离s（千米）与时间t（时）的关系可以用图中的曲线表示。根据图象提供的有关信息，解答下列各题：
⑴ 小明全家在旅游景点游玩了多少小时？
⑵ 求出返程途中s（千米）与时间t（时）的函数关系，并回答小明全家到家是什么时间？
⑶ 若出发时汽车油箱中存油15升，该汽车的油箱总容量为35升，汽车每行驶1千米耗油？升。请你就“何时加油和加油量”给小明全家提出一个合理化的建议。（加油用时忽略不计）
 |
| 阅卷人 |
七、（本题12分）
28. 如图，B为线段AD上一点，△ABC和△BDE都是等边三角形，连结CE并延长交AD的延长线于F，△ABC的外接圆⊙O交CF于M.
⑴ 求证：BE是⊙O的切线；
⑵ 求证：AC2＝CM·CF；
⑶ 若CM＝
，MF＝
，求BD；
⑷ 若过点D作DG∥BE交EF于G，过G作
GH∥DE交DF于H，则易知△DGH是等边三角
形。设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3，试探究S1、S2、S3之间的等量关系，请直接写出其结论。
| 阅卷人 |
八、（本题12分）
29. 抛物线y＝ax2＋bx＋c (a<0)交x轴于A（－1，0）、B（3，0），交y轴于C，顶点为D，以BD为直径的⊙M恰好经过点C.
⑴ 求顶点D的坐标（用a的代数式表示）；
⑵ 求抛物线的解析式；
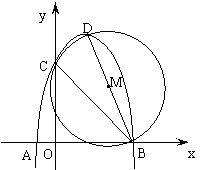⑶ 抛物线上是否存在点P，使△PBD为直角三角形？若存在，求出点P的坐标；若不存在，说明理由。