初中毕业、升学统一考试数学试卷

初中毕业、升学统一考试数学试卷

　　　　　　 　

(考试形式：闭卷　　 试题共五大题25小题　　 卷面分数：120分　 考试时限：120分钟)

考生注意：

本试卷分为两卷，解答第Ⅰ卷时请将解答结果填写在第Ⅱ卷上指定的位置，否则答案无效，交卷时只交第Ⅱ卷。

以下数据和公式供参考：tan63°≈2.0；cot63°≈0.5；；

频率分布直方图中小长方形的面积 = 频率 = ；弧长公式；△=b²－4ac；

　　　　　　　　　　　　 第Ⅰ卷(选择题、填空题　　共46分)

一、选择题(下列各小题都给出了四个选项，其中只有一项是符合题目要求的，请把符合要求的选项前面的字母代号填写在第Ⅱ卷上指定的位置。本大题共10小题，每小题3分，计30分)

1、如果水库的水位高于正常水位2m时，记作+2m，那么低于正常水位3m时，应记作(　　)

(A)+3m　 　　(B)－3m　 　　(C)　+　　　(D)　－

2、下列等式成立的是(　　)

(A)　x²·x³ = x⁶　　 (B)　x³ + x³ = x⁶　 　(C)　(x²)³ = x⁶　　 (D)　(2x³)² = 2x⁶

3、三峡电站的总装机容量是一千八百二十万千瓦，用科学记数法把它表示为(　　)

(A)0.182×10⁸千瓦　　(B)1.82×10⁷千瓦　 (C) 0.182×10^－8千瓦　(D)1.80×10^－7千瓦

4、下列二次根式中与是同类二次根式的是 (　　)

(A)　 (B) 　　(C)　　(D)

5、实数a在数轴上对应的点的位置如图所示，化简a + 3的结果是(　　 )

(A)a + 3　　(B) a－3

(C)－a + 3　　(D)－a－3

6、函数的自变量的取值范围是(　　 )

(A)x≤3　　 (B)x≥3　　 (C)x≤－3且x≠－1　　　(D) x≥－3且x≠－1

7、下列三个命题：①同们角相等，两直线平行；②两点之间，线段最短；③过两点有且只有一条直线，其中真命题有(　　)

(A)0个　 (B)1个　　(C) 2个　　(D) 3个

8、下列用英文字母设计的五个图案中既是轴对称图形，又是中心对称图形的有(　 )

(A) 0个　　(B) 1个　　 (C) 2个　　　　(D)3个

9、若两圆外切，则这两圆的公切线有(　　)

（A）1条　　　（B）2条　　　　（C）3条　　　（D）4条

10、函数y = kx + 1与函数在同一坐标系中的大致图象是（　　　）

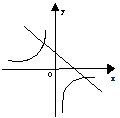
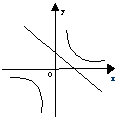
　　　（A）　　　　　　　（B）　　　　　　（C）　　　　　　（D）

二、填空题：（请将答案填写在第Ⅱ卷指定的位置。本大题共4小题，每小题4分，计16分）

11、－2的相反数是___________；

12、三角形按边的相等关系分类如下：

13、若⊙O的半径为4㎝，其中一条弧长为2π㎝，则这条弧所对的圆心角的度数是________；

14、观察下列不等式，猜想规律并填空：

1+ 2>　2×1×2；　　　　　　　　　　　　　　　  （）+（）>　2××

（－ 2）+　3>　2×（-2）×3；　　　　　　　　　   +  > 2××

（－ 4）+　(－3)>　2×（－4）×(－3)；　　　　　　  (－)+ ()> 2××

a + b > _____________(a≠b)

初中毕业升学统一考试

　　　　　　  数学试卷

题号	一	二	三	四	五	总分
得分

第Ⅱ卷　(解答题　　共74分)

一、选择题答案栏：(请将第Ⅰ卷中选择题的答案填写在下表中)

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题答案栏：(请将第Ⅰ卷中填空题的答案填写在下表中)

题号	11	12	13	14
答案

三、解答题：(本大题共5小题，每小题5分，计25分)

15、已知，求代数式的值；

16、已知：如图，AF=CE，AB∥CD，且AB=CD。

　　求证：△CDE≌△ABF

17、如图，有一座石拱桥的桥拱是以O为圆心，OA为半径的一段圆弧。

⑴请你确定弧的中点；(要求：用尺规作图，保留作图痕迹，不写作法和证明)

⑵若∠AOB=120°，OA=4米，请求出石拱桥的高度。

18、已知菱形ABCD中，对角线AC和BD相交于点O，∠BAD=120°，求∠ABD的度数。

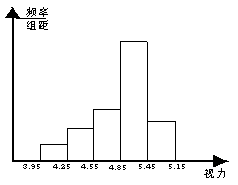19、某市在6000名初中毕业生抽样调查了300名学生的视力，绘制的频率直方图如图，其中

4.85~5.15小组的频率为0.55。

⑴此次抽样视力在4.85~5.15的学生有多少人？

⑵根据用样本估计总体的思想，请你估计这6000名毕业生中，视力在哪一个小组的学生比较多，大约为多少人？

四、解答题：(本大题共3小题，每小题7分，计21分)

20、（本小题提供了两个备选题，请从下面的20－1和20－2题中任选一个予以解答，多做一个题不多计分）

20—1．下面是明明同学的作业中，对“已知关于x方程，判别这个方程根的情况。”一题的解答过程，请你判断其是否正确，若有错误，请你写出正确解答。

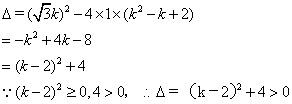解：

∴原方程有两个不相等的实数根。

20－2.如图，一防洪拦水坝的横断面为梯形ABCD，坝顶宽BC＝3米，坝高BE＝6米，坡角α为45°，坡角β为63°，求横断面（梯形ABCD）的面积。

21、如图，PA切⊙O于点A，割线PBC交⊙O于B、C两点，∠APC的平分线分别交AC、AB于D、E两点。请在图中找出2对相似三角形，并从中选择一对相似三角形说明其为什么相似。

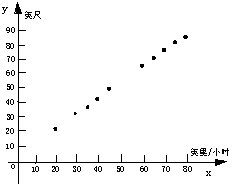
22、汽车行驶中，司机从判断出现了紧急情况到进行刹车时，这一段汽车走过的路程称为刹车反应距离。某研究机构收集了有关刹车反应距离的数据如下表：

x	20	25	30	35	40	45	50	55	60	65	70	75	80
y	22	m	33	38.5	44	50	55	n	66	71	77	82.5	88

表中x为汽车行驶速度（英里/小时），y为刹车反应距离（英尺）；m、n为丢失的数据。由表中给出的有序实数对，在直角坐标系中对应的点如图所示。

⑴请用平滑曲线顺次连结图中各点后，估计y与x的关系最近似于哪一种函数关系，并说明估计的理由；

⑵请利用估计得到的函数关系中，求出表中m、n 的值。

五、解答题：（本大题共小题，23小题8分，24、25小题各10分，计28分）

23、如图，矩形ABCD是一块需探明地下资源的土地，E是AB的中点，EF∥AD交CD于点F，探测装置（设为点P）从E出发沿EF前行时，可探测的区域是以点P为中心，PA为半径的一个圆（及其内部）。当（探测装置）P到达点P₀处时，⊙P₀与BC、EF、AD分别交于G、F、H点。

⑴求证：FD＝FC；

⑵指出并说明CD与⊙P₀的位置关系；

⑶若四边形ABGH为正方形，且三角形DFH的面积为（）平方千米，当（探测装置）P从点P₀出发继续前行多少千米到达点P₁处时，A、B、C、D四点恰好在⊙P1上？

24、知识链接

GPD　　　　 是按市场价格计算的国内生产总值的简称。

百分点　　　是百分比中相当于1％的单位，它是用“和”或“差”分析不同时期百分比的一种表示形式。如，工业总产值今年的增长幅度为19％（也可以说成增长了19个百分点），去年的增长幅度为16％，今年比去年的增长幅度增加了（19－16＝3）3个百分点而不能说成增加了3％。

国债投资　　指国家发行长期建设国债的投资。它已成为经济稳定快速增长的助推器，据测算：每a元钱的国债投资带动的投资总额可以达到4a元至5a元。

问题思考

2002年国债投资带动GDP增长1.7个百分点，创造了120万个就业单位；2002年国债投资1500亿元，创造了150个就业岗位；从2000年到2002年的三年里，由于由国债投资带动GPD增长总共创造了400万个就业岗位。已知2000年与2002年由国债投资带动GPD增长百分点的和，比2001年由国债投资带动GPD增长百分点的两倍还多0.1

⑴若由国债投资带动的投资总额的40％将会转成劳务工资成为城乡居民的收入，请你估计2002年由国债投资带来的城乡居民收入的情况（数额范围）；

⑵若每年GPD增长1.7个百分点就会创造120万个就业岗位，再每增加一个百分点就创造k万个就业岗位。请你确定比例系数k的值，并测算2002年由国债投资带动GPD增长了多少个百分点。

25、已知⊙T与坐标轴有四个不同的交点M、P、N、Q，其中P是直线与y轴的交点，点Q与点P关于原点对称。抛物线经过点M、P、N，其顶点为H。

⑴求Q点的坐标；

⑵指出圆心T一定在哪一条直线上运动；

⑶当点H在直线上，且⊙T的半径等于圆心T到原点距离的倍时，你能确定k的值吗？若能，请求出k的值；若不能，请你说明理由。

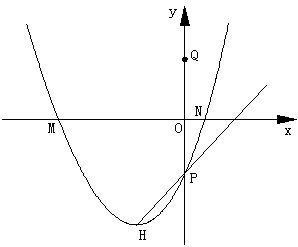（第25题图供分析参考用）