初中毕业、升学统一数学考试

初中毕业、升学统一数学考试

数　　　学

注意事项：1.全卷满分120分考试时间120分钟，共3页，32道题．

　　　　  2.考生在答题过程中。可以使用CZ1206型函数计算器，若试题计算结果没有要求取近似值，则计算结果取精确值（或保留根号）。

　　　　  3.用钢笔或圆珠笔直接答在试卷上

　　　　  4.答卷前将密封线内的项目填写清楚，并将座位号填写在试卷规定的位置上．

一、 填空题（第1—6题每格1分，第7—9题每格2分，共18分）

1、-8的立方根是　　　　　　 ；　　　　　　 ；=　　　　　  。

2、已知一元二次方程的两个根是，，则　　　，　　　　，　　　  。　　　　　　　　　 

3、　　　　　　　　　　　  如图，梯形ABCD中，AD∥BC，G、F、E、H分别是边AB、BC、CD、DA的中　点，梯形ABCD的边满足条件　　　　　  时，四边形EFGH是菱形。

　　　　　　　　　　　 

4、　　　　　　　　　　　  如图，PA切⊙O于点A，割线PBC交⊙O于点B、C，若PA=6，PB=4，AB的

　　　　　  度数为60°，则BC=　　　 　　，∠PCA=　　　　  度，∠PAB=　　　　  度。

　　　

如图，直线AE∥BD，点C在BD上，若AE=5，BD=8，△ABD的面积为16，

5、　则△ACE的面积为　　　　　　　  。

　

6、三峡一期工程结束后的当年发电量为55亿千瓦时，某市10万户居民平均每户年用电量2750千瓦时，则三峡工程该年所发电能可供该市居民使用　　　　　　　 年。

7、请写出一个根为，另一根满足的一元二次方程　　　　　　　　　  。

8、用计算机探求：满足不等式的最小正整数　　　　　　  。

9、　 光线以图所示的角度α照射到平面镜Ⅰ上，然后在平面镜Ⅰ、Ⅱ之

　　　 间来回反射，已知∠α=60°，∠β=50°，∠γ=　　　　　　 度。

二、 选择题　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　

（下列各题都给出代号为A、B、C、D的四个答案，其中有且只有一个是正确的，把正确答案的代号填在

【　】内，每题2分，共18分）

10、一元二次方程的根的情况是　　　　　　　　　　　　　　　　　　　 【　　　】

（A）有两个相等的实数根　　　　　　　  （B）有两个不相等的实数根，且两根同号

（C）有两个不相等的实数根，且两根异号　（D）没有实数根

11、若，则的取值范围是　　　　　　 （　　　）

（A）　　　 （B）　　　 （C）　　　 （D）　　　　　 

12、已知关于的不等式的解集如图所示，　

则的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 【　　　】

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（A）2　　　　　  （B）1　　　　　  （C）0　　　　　  （D）-1

13、式子、、、中，有意义的式子个数为　　 【　　　】

（A）1个　　　　 （B）2个　　　　  （C）3个　　　　 （D）4个

14、两圆的半径分别为3和5，圆心距为2，则两圆的位置关系是　　　　　　　　　　　　 【　　　】

（A）外切　　　　　 （B）内切　　　　　 （C）相交　　　（D）内含

15、已知正三角形的边长为6，则该三角形的外接圆半径为　　　　　　　　　　　　　　  【　　　】

（A）　　　　  （B）3　　　　　　  （C）　　　　  （D）1

16、　　　　　　　　　　　　　  某人骑车外出，所行的路程S（千米）与时间t（小时）的函数

关系如图所示，现有下列四种说法：

 ①第3小时中的速度比第1小时中的速度快；

 ②第3小时中的速度比第1小时中的速度慢；

 ③第3小时后已停止前进；

 ④第3小时后保持匀速前进。

其中说法正确的是　　　　　　　　　　　 【　　　】

（A）②、③　　　 （B）①、③　　　　 （C）①、④　　　 （D）②、④

17、　　　　 如图：矩形花园ABCD中，，，花园中建有一条

矩形道路LMPQ 及一　条平行四边形道路RSTK。若，

则花园中　可绿化部分的面积为　　　　　　　　　　　 【　　　】

（A）　　（B）

（C）　　（D）

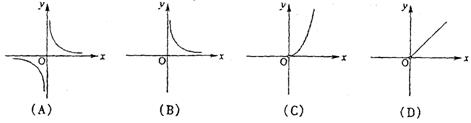
18、已知圆柱的侧面积是，若圆柱底面半径为，高为，则关于的函数

图象大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 【　　　】

　　　　　　　 

三、（每题4分，共16分）

19、不用计算器求值：　　　　　　　　　  　20、计算：

21、解不等式组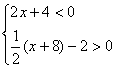：　　　　　　　　　　　  22、解方程组：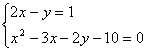

四、（第23题4分，第24题6分，共10分）

23、为了解各年龄段观众对某电视剧的收视率，某校初三（1）班的一个研究性学习小组，调查了部分观众的收视情况并分成A、B、C、D、E、F六组进行整理，其频率分布直方图如图所示，请回答：

（1） E组的频率为　　　　  ；若E组的频数为12 ，则　　　被调查的观众数为　　　　人；

（2）补全频率分布直方图；

（3）若某村观众的人数为1200人，估计该村50岁以上的观众有　　　　　　  人。

24、已知二次函数的图象经过点（2，0）、（-1，6）。

（1）求二次函数的解析式；

（2）画出它的图象；

（3）写出它的对称轴和顶点坐标。

五、（每题6分，共12分）

25、如图，已知AB是⊙O的直径，C是⊙O上一点，连接AC，过点C作直线

 CD⊥AB于点D，E是AB上一点，直线CE与⊙O交于点F，连结AF，与

直线CD交于点G。

求证：（1）∠ACD=∠F；　（2）AC²=AG·AF。

26、如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上

图中有　　　　　　　　 对四边形面积相等；

他们是　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　 

　 　　　　　　　　　　　　　　　　　　　 。

六、（每题6分，共12分）

27、如图，已知点A（2，3）和直线，

（1）读句画图：画出点A关于直线的对称点B，点A关于原点（0，0）的对称点C；

（2）写出点B、C的坐标　　　　　　　　 ；

（3）判断△ABC的形状，并说明理由。

28、甲、乙两班学生到集市上购买苹果，，苹果的价格如下：

购苹果数	不超过30千克	30千克以上但不超过50千克	50千克以上
每千克价格	3元	2.5元	2元

甲班分两次共购买苹果70千克（第二次多于第一次），共付出189元，而乙班则一次购买苹果70千克。

（1）乙班比甲班少付多少元？

（2）甲班第一次、第二次分别购买苹果多少千克？

七、（每题8分，共16分）

当你进入博物馆的展览厅时，你知道站在何处观赏最理想？

如图，设墙壁上的展品最高处点P距离地面a米，最低处点Q距离地面b米，观赏者的眼睛点E距离地面m米，当过P、Q、E三点的圆与过点E的水平线相切于点E时，视角∠PEQ最大，站在此处观赏最理想。

（1）设点E到墙壁的距离为x米，求a、b、m、x的关系式；

（2）当a=2.5，b=2，m=1.6，求：

（ⅰ）点E和墙壁距离x；

（ⅱ）最大视角∠PEQ的度数（精确到1度）。

30、如图，正三角形ABC的边长为1cm，将线段AC绕点A顺时针旋转120°至AP₁，形成扇形D₁；将线段BP₁绕点B顺时针旋转120°至BP₂，形成扇形D₂；将线段CP₂绕点C顺时针旋转120°至CP₃，形成扇形D₃；将线段AP₃绕点A顺时针旋转120°至AP₄，形成扇形D₄……。设为扇形D_n的弧长（n=1，2，3……）,回答下列问题：

（1）按照要求填表：

n	1	2	3	4

（2）根据上表所反映的规律，试估计n至少为何值时，扇形D_n的弧长能绕地球赤道一周？（设地球赤道半径为6400km）。

八、（第31题8分，第32题10分，共18分）

31、如图，直线OC、BC的函数关系式分别为和，动点P（x，0）在OB上移动（0<x<3），过点P作直线与x轴垂直。

（1）求点C的坐标；

（2）设△OBC中位于直线左侧部分的面积为s，写出s与x之间的函数关系式；

（3）在直角坐标系中画出（2）中函数的图象；

（4）当x为何值时，直线平分△OBC的面积？

32、设一次函数的图象为直线，与x轴、y轴分别交于点A、B。

（1）求tan∠BAO的值；

（2）直线m过点（-3，0），若直线、m与x轴围成的三角形和直线、m与y轴围成的三角形相似，求直线m的解析式。