初三数学阶段测试试题（五）
命题人:刘欣 校对人:刘欣
(考试时间:2004年2月28日)
一、选择题（3′× 14 = 42′）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 答案 |
1、函数 
中自变量x的取值范围是
A、x≤
且x≠0
B、x>且x≠0
C、x≠0 D、x< 且x≠0
2、某校为了解360名初一学生体重情况，从中抽取60名学生进行测量，下列说法正确的是
A、总体是360 B、个体是该校初一的每个学生 C、样本是所抽取的60名学生 D、样本容量是60
3、在所给一组数据中,有m个x1,有n个x2,有p个x3,那么这组数据的平均数是
A、
B、
C、
D、
4、已知，正比例函数y=(2m-1)x的图象上有两点A(x1,y1)，B(x2,y2)，当x1<x2时，有y1>y2，则m的取值范围是
A、m<
B、m>
C、m<2
D、m>2
5、如图，图中的五个半圆，邻边的两个半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿弧ADX、弧XEY、弧YFZ、弧ZGB路线爬行，乙虫沿弧ACB路线爬行，则下列结论正确的是
A、甲先到B点 B、乙先到B点 C、甲、乙同时到B点 D、无法确定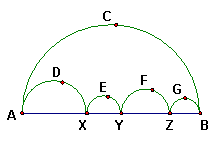
（题5） 
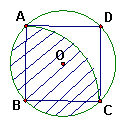（题8）
6、矩形纸片ABCD,AB=6cm,AD=2cm,用它做成圆柱的侧面,则圆柱的底面半径是
A、
cm B、6cm C、
D、6cm或3cm
7、当x<0时，函数y=x和
在同一直角坐标系中的大致图象是
8、如图，⊙O的半径为R，以圆内接正方形ABCD的顶点B为圆心，AB为半径，画弧AC，则阴影部分的面积为
A、
B、
C、
D、
9、下列说法正确的是
A、3、4、3、4、5、5、5、2这组数据的众数是3；
B、为了解参加运动会的运动员的年龄情况，从中抽查了100名运动员的年龄，这里100名运动员是抽取的一个样本；
C、如果数据x1,x2,…,xn的平均数是
，那么
；
D、一组数据的方差是s2，将这组数据中的每个数据都乘以3，所得到的一组新数据的方差是3s2。
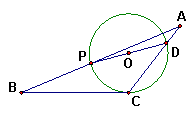
10、如图，已知直线BC切⊙O于点C，PD为⊙O直径，BP的延长线与的CD延长线交于点A，∠A=28º,∠B=26º,∠PDC等于
A、34º B、36º C、38º D、40º
11、如图,⊙O1、⊙O2、⊙O3两两相切于P,A、B两点在⊙O1上,C、D两点在⊙O2上,E、F两点在⊙O3上,则下列结论①弧AP与弧PD内连接②弧AP与弧PF外连接③弧PE与弧PD外连接④弧PD与弧PF外连接⑤弧AP与弧PC内连接，正确的是
A、①②③ B、①③④ C、③④⑤ D、全正确
（题10） 
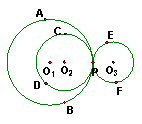（题11）
12、无论m为何实数，直线y=x+2m与y=-x+4的交点都不可能在
A、第一象限 B、第二象限 C、第三象限 D、第四象限
13、如图，两个同心圆，大圆半径为5cm，小圆半径为2cm，与大圆内切且与小圆内切的圆的半径是
A、6 cm B、7 cm C、7.5 cm D、3.5cm
14、正六边形ABCDEF中，阴影部分面积为
cm2，则此正六边形的边长为
A、2cm B、4cm C、6cm D、8cm
（题13）
（题14）
二、填空题（3′× 13 = 39′）
15、已知圆锥的底面半径为2cm，母线长为6cm，则这个圆锥的侧面积是____________。
16、圆内接四边形ABCD，∠A∶∠B∶∠C=2∶4∶7，则∠D=_______________。
17、等腰△ABC周长为10，底边BC长为y，腰AB长为x
（1）写出y关于x的函数关系式_______ ___。
（2）x的取值范围_______________。
18、已知二次函数
有最大值为1,则m的值为_____________。
19、一组数据为a，m，n，a，a，b，m，n，m，a，且a<b<m<n，则这组数据的中位数是_______________，众数是_______________。
20、①各边相等的圆内接多边形是正多边形②各角相等的圆内接多边形是正多边形③各边相等的圆外切多边形是正多边形④各角相等的圆外切多边形是正多边形
其中正确的命题有_______________。
21、把抛物线向左平移2个单位，在向下平移3个单位，得到抛物线
，则原抛物线的解析式为_______________。
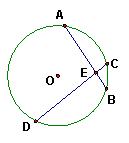
22、已知（如图）⊙O的弦AB、CD相交于点E，弧AC的度数为60º，弧BD的度数为100º，则∠AEC=_______________。
23、如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上的两点，如果∠E=46º，∠DCF=32º，则∠A的度数是______________。
（题22） 
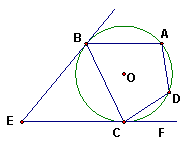（题23）
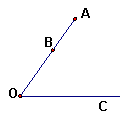
24、已知，如图，∠AOC=60º，点B在OA上，且OB=
，若以B为圆心，R为半径的圆与射线OC只有一个交点，则R的取值______________。
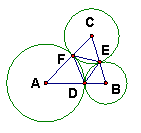
25、如图，⊙A，⊙B，⊙C之间两两相切，切点为D、E、F，则过D、E、F三点的圆的圆心是△ABC的______________。
（题24）
（题25）
三、解答题（8′+7′+8′+8′+8′+8′+10′+12′=69′）
26、已知直线y=2x+1，（1）求该直线与x轴，y轴的交点坐标；
（2）若直线y=kx+b与已知直线关于x轴对称，求该对称直线的解析式。
27、已知二次函数y=ax2-2的图象经过点（1，-1），求这个二次函数的解析式，并判断该函数图象与x轴的交点个数。
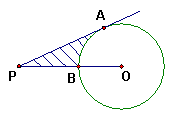28、如图，已知PA切⊙O于A点，OP交⊙O于B点，PA=
，PB=5，求PA、PB和弧AB所围成的图形的周长和面积。
29、甲、乙两人在相同条件下各射靶10次，每次射靶的成绩如图所示：
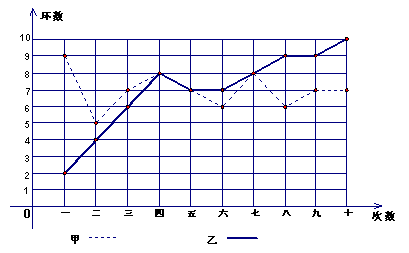
（1）请填写下表：
| 平均数 | 方 差 | 中位数 | 命中9环以上次数 | |
| 甲 | 1.2 | 7 | 1 | |
| 乙 | 5.4 |
（2）请从下列四个不同角度对这次测试结果进行分析：
①从平均数和方差相结合看（谁的成绩较稳定）；
②从平均数和中位数相结合看（谁的成绩好些）；
③从平均数和命中9环以上的次数相结合看（谁的成绩好些）；
④从折线图上两人射击命中环数的走势看（分析谁更有潜力）。
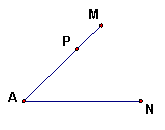30、已知如右图，∠MAN和其一边上的点P。
（1）作一个圆使它和∠A的两边都相切且其中一个切点是P,另一个切点是Q（保留作图痕迹,不写作法）
（2）指出与弧PQ连接的线段。
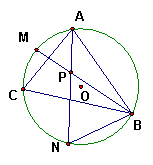31、已知，如图，△ABC内接于⊙O，N为弧BC的中点，M为弧AC的中点，AN与BM交于点P。
求证：NB=NP。
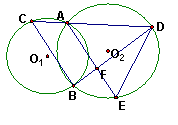32、如图，⊙O1与⊙O2相交于两点A和B，过B点作的⊙O1切线交⊙O2于D点，连结DA并延长与⊙O1相交于C点，连结BC，过A作AE∥BC与⊙O2相交于E点，与BD相交于F点。
（1）求证：EF•BC=DE•AC ；
（2）若AD=3，AC=1，AF=
，求EF的长。
33、已知：抛物线y=a(x-t-1) 2+t2(a,t是常数且a≠0,t≠0)的顶点为A，抛物线y=x2-2x+1的顶点是B。
（1）判断点A是否在抛物线y=x2-2x+1上，为什么？
（2）如果抛物线y=a(x-t-1) 2+t2(a,t是常数且a≠0,t≠0)经过点B.
①求a的值；②这条抛物线与x轴的两个交点和它的顶点A能否构成直角三角形？若能，求出t的值；若不能，说明理由。
初三月考数学（五）试题答案
一 选择：A D C AC C B A C B A C D B
二 填空题：15、12
16、100º 17、y=10-2x，
<x<5
18、m=0 19、
，a 20、①④ 21、
22、80º 23、99º 24、R=3或R> 25、内心
三解答题：26、
、（0，1）、y=-2x-1 27、y=x2-2，2个
28、周长
、面积
29、（1）7，7，7.5，3
（2）①甲稳定②乙好③乙好④乙有潜力 30、线段PM、QN
31、证∠NPB=∠NBP 32、（1）△ACB∽△EFD（2）BD=2、
EF=
33、（1）在（2）①a=-1②B（1，0），设C（2t+1，0）
当C在B左边，有t2=1-（t+1），t=-1或0（舍）；当C在B右边。有t2=（t+1）-1，t=1或0（舍），∴t=1或-1