初三数学模拟试卷
2003.5
第一部分（满分100分）
一、填空题（每空2分，共24分）
1.方程2y－1＝0的根是 ；0.0310含有 个有效数字；
2.函数y＝2x－3的图象与x轴交点为 ；函数y＝（x－1）2＋2的图象与y轴交点为 ；对于函数y＝－，当x＜0时，这部分图象在第 象限，
3.正方形的内切圆与外接圆的面积之比为 ；
4.高60米的塔影长为40m，同一时刻，高3米的树干影长 米。
5.等腰三角形的一个底角为30°，一腰长是6，则它的底边上的高是 ；外接圆的半径是 ；
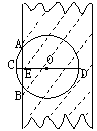6.圆锥的底面半径是4cm，侧面积是20πcm2，则圆锥的高是
cm，侧面展开图中扇形的圆心角是
；
7.“圆材埋壁”是我国古代著名的数学著作《九章算术》
中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，
深一寸（CE＝1），锯道（注：即图中AB）长十寸，问径（注直
径）＝ 寸。”
二、选择题（每小题3分，共18分，每小题只有一个正确答案）
8.（－a）2·a÷a2等于（ ）
A.－1 B.1 C.a D.a2
9.若－1＜a＜1，则 ＋a＋1等于（ ）
A.2 B.2a C.2a＋2 D.2a－2
10.若两圆有且只有两条公切线，则这两圆的位置关系是（ ）
A.外离 B.外切 C.相交 D.内切
11．已知一组数x1，x2，x3，x4，x5的平均数是2，方差是，那么另一组数据3x1－2，
3x2－2，3x3－2，3x4－2，3x5－2的平均数和方差分别是（ ）
A.2， B.2，1 C.4， D.4，3
12.若0＜a＜1，则抛物线y＝（x＋1－a）2＋a的顶点在（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.如图，Rt△ABC中，∠BAC＝90°，D是BC中点，AE⊥AD交CB延长线于点E，则结论正确的是（ ）
A.△BAE∽△ACB B.△AEB∽△ACD
C.△AEC∽△DAC D.△BAE∽△ACE
三、简答题（每小题6分，共24分）
14.｜tan45°－｜－（－）0－－＋（）－1
15.解方程－＋2＝0
16.某校初三年级学生参加“抗击非典捐款”活动，甲班共捐款200元，乙班30名同学共捐款200元，这样两班人均捐款比甲班人均捐款多1元，问甲班有多少人参加捐款，（规定每班人数不超过54人）。
17.甲乙两小组各10名学生某次数学测验成绩如下（单位：分）
甲组：76，90，84，86，81，87，86，82，85，83
乙组：82，84，85，89，79，80，91，89，78，74
回答下列问题：
⑴甲组数据的众数为 ；乙组数据的中位数为 ；
⑵经计算：S甲2＝13.2，S乙2＝26.36，S甲2＜S乙2这说明 （用文字语言表达）
⑶将甲乙两组数据合并成一组数据后，按照组距4分分组时，可以分成以下5组，
73.5～77.5，77.5～81.5，81.5～85.5，85.5～89.5，89.5～93.5，则其中85.5～89.5这一组的频数是 ；频率是 ；
四、证明计算（18-20题每小题8分，21题10分，共34分）
18.如图，ABCD为正方形，E是BC上一点，AE交BD于F，连CF，
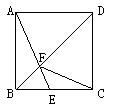求证：∠DCF＝∠BEA
19.为了响应节水号召，小红家要使200m3的水比过去多用5个月，计划每月比过去用少2m3，问小红家计划每月用多少水？
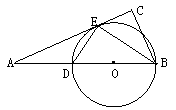20.如图，△ABC中，∠C＝90°，BE平分∠ABC，DE⊥BE，交AB于D，⊙O是△BDE的外接圆，⑴求证：AC是⊙O的切线；⑵若AD＝6，AE＝6，求DE。
21.如图，以P（3，0）为圆心，5为半径的圆交x轴于A、B，交y轴于C、D
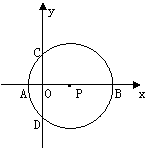⑴求过A、B、C三点的抛物线的解析式：
⑵若⑴中抛物线的顶点为M，判定直线MC
与⊙P的位置关系，并说明理由：
⑶过点B作QB⊥AB交直线MC于点Q，问P、
Q、D三点是否在同一直线上，为什么？
第二部分（满分50分）
五、选择题（每小题3分，共15分，每小题只有一个正确答案）
22.在△ABC中，a，b分别是∠A、∠B的对边，如果sinA:sinB＝2:3，则a:b等于（ ）
A.2:3 B.3:2 C.4:9 D.9:4
23.有一旅客携带了30kg行李从南京禄口国际机场乘飞机去天津，按民航规定，旅客最多可免费携带20kg行李，超重部分每公斤按飞机票价格的1.5%购买行李票，现该旅客购买了120元的行李票，则他的飞机票价格应是（ ）
A.1000 B.800 C.600 D.400
24.若x＝1时，px3＋qx＋1＝2003，则当x＝－1时，Px3＋qx＋1＝（ ）
A.2001 B.2003 C. －2001 D.－2003
25.如果a是一元二次方程x2－3x＋m＝0的一个根，如果－a是一元二次方程x2＋3x－m＝0的一个根，那么a的值是（ ）
A.1或2 B.0或－3 C.－1或－2 D.0或3
26.如图，直线AB经过⊙O的圆心，与⊙O相交于A、B两点，
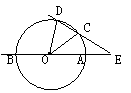点C在⊙O上，且∠AOC＝30°，点E是直线AB上的一个动点（与
点O不重合），直线EC交⊙O于D，则使DE＝DO的点E共有（ ）
A.1个 B.2个 C.3个 D.4个
六、（本题8分）
27.已知实数a，b满足a2＝2－2a，b2＝2－2b，且a≠b，求：⑴＋的值；
⑵a2＋2b2＋2b的值。
七、（本题7分）
28.在一服装厂里有大量形状为等腰直角三解形的边角布料（如下图）现找出其中的一种，测得∠C＝90°，AC＝BC＝8，今要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好都在△ABC的边上，且扇形的弧与△ABC的其它边相切。
请设计出所有可能符合题意的方案示意图，并求出扇形的半径（只要求画出图形，并直接写出扇形半径）
八、（本题10分）
29.已知：如图，PA切⊙O于A，割PBC线交⊙O于B、C，PD⊥AB于D，延长PD交AO的延长线于E，连结CE并延长交⊙O于F，连结AF。
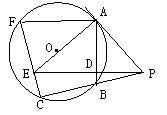⑴求证：PD·PE＝PB·PC
⑵求证：PE∥AF；
⑶连AC，若AE:AC＝1:，AB＝2，求EF的长。
九、（本题10分）
30.如图，在平面直角坐标系xoy中，正方形OABC的边长为2厘米，点A、C分别在y轴的负半轴和x轴的正半轴上。抛物线y＝ax2＋bx＋c经过点A和点B，且12a＋5c＝0
⑴求抛物线的解析式
⑵如果点P由点A开始沿AB边以2厘米/秒的速度向点B移动，同时点Q由点B开始沿BC边以1厘米/秒的速度向点C移动。移动开始后第t秒时，设S＝PQ2（厘米2）
①试写出S与t之间的函数关系式，并写出t的取值范围；
②当S取最小值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出点R的坐标；如果不存在，请说明理由。
 |