初三数学能力训练
A组
一、判断正误
1． 
的立方根是
和－
；（ ） 2．7的平方根是±49；（ ）
3． 
是3的算术平方根；（ ）
4． 
是
的立方根；（ ）
5．无限小数是无理数；（ ） 6．任何实数既有平方根，也有立方根；（ ）
7．无理数的和、差、积、商仍是无理数；（ ）
8．无论m取任何实数，根式
都有意义；（ ）
9．数轴上的所有点都对应着有理数；（ ） 10．设a是实数，则
① 
；（ ）② 
；（ ）③ 
；（ ）④ 
；（ ）⑤ 
；（ ）
二、填空题
11．和数轴上的点一一对应的数集是
. 12．小于 
而大于
的自然数是 .
13．小于 
而大于
的整数是 . 14．平方根的绝对值与自身相等的数是
.
15． 
的相反数是 ，倒数是 ，绝对值是 ，负倒数是 ，平方是 ，平方根是 ，算术平方根是 .
16．若 
，化简
.17． 
18．若 
与
互为相反数，则
19．（1）如果一个正数的平方根是a，那么它的另一个平方根是 . （2）1的平方根是 ，－2的平方根是 .
20．（1）若 
，则x
. （2）如果 
的平方根是±3，那么 
三、选择题
21．下列命题中错误的命题是（ ）
A．1.44的平方根是1.2 B．－1.2是1.44的平方根
C．1.44的负平方根是－1.2 D．1.2是1.44的正的平方奶
22．已知下列各数：
3.1416， 
，0.， 
，π，
，其中无理数的个数是（ ）
A．0 B．1 C．2 D．3
23．和数轴上的点一一对应的数是（ ）
A．整数 B．有理数 C．无理数 D．实数
24．下列实数中，有理数的个数有（ ）
π， 
，
，－0.…， 
.
A．2个 B．3个 C．1个 D．4个
25．“25的平方根是±5”的表达式是（ ）
A． 
B． 
C． 
D． 
26．下列说法正确的是（ ）
A．9的算术平方根是±3 B．4是16的算术平方根
C．0.4是1.6的算术平方根
D． 
的算术平方根是－5
27．若 
，则
（ ）
A．0.01412 B．0.1412 C．0.04462 D．0.4462
28． 
的平方根是（ ）
A．16 B．±16 C．4 D．±4
29．在实数范围内，下列判断正确的是（ ）
A．若 
，则
B．若 
，则
C．若 
，则
D．若 
，则
30．用四舍五入法，0.02046（保留两个有效数字）应为（ ）
A．0.02 B．0.020 C．0.021 D． 
31．现有四个无理数： 
、
、
、
，其中在实数
与
之间的有（ ）
A． B． 和
C． 和
D． 和
32．计算 
的值为（ ）
A．21 B．30 C．39 D.31
33．生物学家指出：生态系统中，每输入一个营养级的能量，大约只有10％的能量能够流动到下一个营养级.在 
这条生物链中（
表示第个营养级，
1，2，…，6），要使
获得10千焦的能量，那么需要 提供的能量约为（ ）.
（A） 
千焦 . (B) 
千焦 . (C) 
千焦. (D) 
千焦.
B组
1．已知a、b为实数，且 
，求
的值.
2．已知 
，求代数式
的值.
3．求下列各式的值：
（1） 
； （2） 
； （3） 
； （4） 
； （5） 
； （6） 
.
4．下列命题是否为真命题？为什么？
（1）若 
，则
； （2）若a为任意实数，则 
；
（3）如果 
，则
.
5．回答下列问题：
（1）若3m－5与－2m＋1互为相反数，求m的值；（2）若3m－5与－2m＋1互为倒数，求m的值；
（3）是否存在使 
的m的值？为什么？
6．若 
，求
的值.
7．计算：
（1） 
；
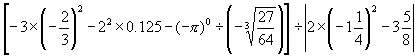（2） 
.
8．若 
，求
.
9．计算：
（1） 
； （2） 
.
10．到火星旅行，来回的行程需要三个地球年（包括在火星上停留449个地球天），已知火星和地球之间的距离为千米，那么，这个旅行的平均速度是每小时多少千米？（说明：地球年、地球天是指在地球上的一年或一天）
11．（1）阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为 AB.
当A、B两点中有一点在原点时，不妨设点A在原点, 如图1, AB= OB= b=a-b;
当A、B两点都不在原点时：
① 如图2，点A、B都在原点的右边， AB= OB— OA= b— a=b—a= a—b；
② 如图3，点A、B都在原点的左边， AB= OB— OA= b— a=—b—（—a）= a—b；
③ 如图4，点A、B都在原点的左边， AB= OB+ OA= b+ a= a+（—b）= a—b.
综上，可知数轴上A、B两点之间的距离 AB= a—b.
（2）回答下列问题：
① 数轴上表示2和5的两点之间的距离是 ，数轴上表示
和
的两点之间的距离是 ，数轴上表示1和 
的两点之间的距离是 ；
② 数轴上表示 
和
的两点A和B之间的距离是
，如果 AB=2，那么 为 ；
③ 当代数式 +1+
—2取最小值时，相应的 的取值范围是 .
参考答案
A组
一、×、×、√、×、×、×、×、√、× 10．①×、②×、③×、④×、⑤√
二、11．实数集 12．4、3、2、1 13．3、2、1、0、－1、－2 14．1、0
15． 
16．－4a 17．
18． 
19．（1）－a；（2）±1，不存在. 20．（1）0，（2）81
三、21．A 22．B 23．D 24．B 25．C 26．B 27．B 28．D 29．D 30．B
31．C 32．A 33. C
B组
1．提示：由已知， 
解得 
2．提示：由已知， 
解得 
.
3．（1）5；（2）－1；（3）3；（4）－4；（5）2；（6）2.
4．（1）假命题；（2）假命题；（3）真命题.
5．（1） 
；（2） 
或
；（3）不存在.
6．提示： 
当
时，
；当时
时，
；当
时，
，当
时，
.
7．（1）原式＝－1；（2）原式 
.
8．提示： 可变形为
.
解得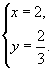 
.
9．（1）提示：原式 
.
（2）提示：设 
.则
原式 
＝＋1997＝.
10． 
.
11．（1）3、3、4；（2）x+1 、1或
；（3） 
.