初三数学上期第二次月考数学试卷
一、选择题: 本大题共10小题；每小题2分，共20分，在每小题给出的四个选项中，只有一项是符合题目要求的．请将答案序号填入答题卡中。
1．
化简的结果是【 】
A．2 B．—2 C．2或—2 D．4
2．点P（－2，3）关于原点对称点的坐标是【 】
A．（－2，3） B．（2，－3） C．（2，3） D．（－2，－3）
3．如图1，△ABC中，∠C=90°，BC=2，AB=3，则下列结论正确的是【 】
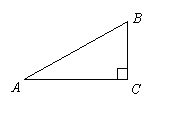A．
B．
|
D．
4．如果两个圆只有一条共切线，那么这两个圆的位置关系是【 】
A．外离 B．外切 C．相交 D．内切
5．下列图形中，轴对称图形的个数是【 】
A．1个 B．2个 C．3个 D．4个．
6．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打【 】
A．6折
B．7折 C．8折 D．9折
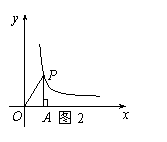
7．如图2，P是反比例函数
在第一象限分支上的一动点，PA⊥x轴，随着x逐渐增大，△APO的面积将【
】
A．增大 B．减小 C．不变 D．无法确定
8．为了鼓励节约用水，按以下规定收取水费：（1）每户每月用水量不超过20立方米，则每立方米水费1.2元，；（2）
每户每月用水量超过20立方米，则超过部分每立方米水费2元，设某户一个月所交水费为y（元），用水量为x（立方米），则y与x的函数关系用图像表示为【 】
 |
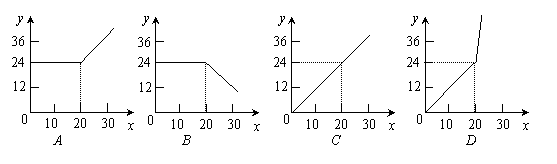9．如下图中的四个正方形的边长均相等，其中阴影部分面积最大的图形是【 】
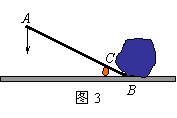10．如图3，是用杠杆撬石头的示意图，C是支点，当用力压杠杆的端点A时，杠杆绕C点转动，另一端点B向上翘起，石头就被撬动．现有一块石头，要使其滚动，杠杆的B端必须向上翘起10cm，已知杠杆的动力臂AC与阻力臂BC之比为5︰1，则要使这块石头滚动，至少要将杠杆的端点A向下压【 】
A、100cm B、60cm
C、50cm D、10cm
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案号 |
二、填空:本大题共10小题；每小题2分，共20 分．把答案填写在题中横线上．
11．－5的倒数是
12．分解因式：
=
．
13．写出一个反比例函数的解析式，使它的图像不经过第一、三象限：
．
14．四边形ABCD是菱形，∠A=60°，对角线BD的长为7cm，则此菱形的周长是 cm．
15．用换元法解方程
，若设
，则原方程可化为
．
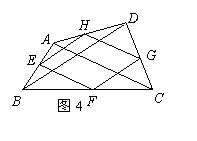
16．如图4，顺此连接四边形ABCD各边中点，得到四边形EFGH，还需添加 条件，才能保证四边形EFGH是矩形
17．如图5，A、B、C三点是⊙O上的点，∠ABO=55°, 则∠BCA
的度数是
度．
18．等腰梯形中，已知一底角是45°，高为1，中位线长
为3，则梯形的上底长为
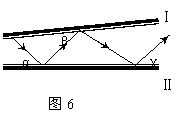
19．光线以如图6所示的角度α照射到平面镜上，然后在
平面镜Ⅰ、Ⅱ间来回反射，已知α=60°，β=50°，
则γ= 度．
20．某建筑工地急需长12cm和17cm两种规格的金属线材，现工地上只有长为100cm的金属线材，要把一根这种金属线材截成12cm和17cm的线材各 根时，才能最大限度地利用这种金属线材．
三、计算（本题共8个小题，共80分）
21．(本小题满分8分)
先化简，在求值：
，其中
．
22．(本小题满分8分)
如图7，ABCD是正方形，点E在BC上，DF⊥AE于F．请你在AE上找一点G，
使△ABG≌△DAF，并给予证明．
23．(本小题满分8分)
如图8，PA切⊙O于点A，PBC交⊙O于点B、C，若PB、PC的长是关于x的方程
的两根，且BC=4，求m的值以及PA的长．
24. (本小题满分12分)
甲、乙两名同学进行投掷飞镖比赛，每人各投掷10次，中靶情况如图9所示．
|
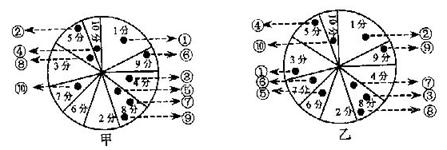
请你回答下列问题
（1）填写下表：
| 分数 | 1分 | 2分 | 3分 | 4分 | 5分 | 6分 | 7分 | 8分 | 9分 | 10分 |
| 甲（次数） | ||||||||||
| 乙（次数） |
（2）分别写出甲、乙两名同学这10次投掷飞镖
比赛成绩的平均数、中位数和众数
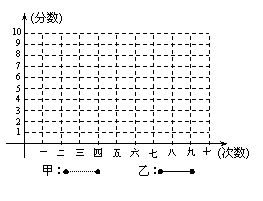
（3）在右图的网格图中，画出甲、乙投掷飞镖
成绩的折线图
（4）从折线图的走势看，请你分析哪位同学的潜力较大．
25．(本小题满分12分)
某运输部门规定：办理托运，当一件物品的重量不超过a千克（a＜18）时，需付基础费30元和保险费b元；为了限制过重物品的托运，当一件物品超过a千克时，除了付以上基础费和保险费外，超过部分还需每千克付c元的超重费．设某件物品的重量为x千克，支付费用为y元．
（1）当0＜x≤a时，y= (用含b的代数式表示)；
当x＞a时，y= (用含a、b、c的代数式表示)；
（2）甲、乙、丙三人各托运一件物品，物品的重量与支付费用如下表所示：
| 物品重量（千克） | 支付费用（元） |
| 12 | 33 |
| 18 | 39 |
| 25 | 60 |
①是根据以上提供的信息确定a、b、c的值，并写出支付费用y（元）与每件物品重量x（千克）的函数关系式
②试问在物品可拆分的情况下，用不 超过120元的费用能否托运50千克的物品？若能，请你设计出一种托运方案；若不能请你说明理由．
26．(本小题满分12分)
已知在△ABC中，AB=AC，AD⊥BC于D，且AD=BC=4，若将此三角形沿AD剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有的不同形状的四边形吗？画出所拼四边形的示意图（表出图中的直角），并分别写出所拼四边形的对角线的长（不要求写计算过程，只需写出结果即可）
 |
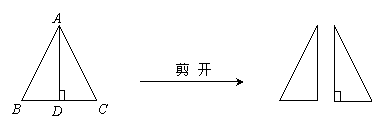27、(本小题满分12分)
某电脑软件经销店，以每件30元的进价购进一种新开发的软件W,通常销售利润可达到进价的60%.为促进商店内与软件W相关联的其它软件(销售价格不变)的销售，决定将软件W在不赔本的情况下,每件的销售利润以不高于进价30%的可变价格出售，用来招揽顾客.经过几天销售发现，其它软件日均销售利润
元与软件W的售价x元满足一次函数关系，当软件W的售价分别是33元和38元时，其它软件的销售利润分别是188元和168元.
（1） 求出y与x的函数关系式，并写出
的取值范围；
（2） 若在一天中，能将19件软件W售出，销售软件W与销售其他软件的利润和不低于230元，试确定软件W的售价范围.（利润＝售价—进价）
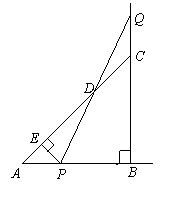
28、(本小题满分12分)
等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交与点D．设P点运动时间为t，△PCQ的面积为S．
(1)求出S关于t的函数关系式
(2)当点P运动几秒时，S△PCQ=S△ABC
(3)作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论．
 |