初三数学第二轮总复习

初三数学第二轮总复习--第十一讲 基本题型之四：探索型题

杨建

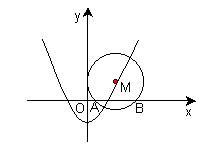
【中考题特点】：

近年来全国各地中考试题中频频出现探索型问题，这类问题由于没有明确的结论，要求考生通过自己的观察、联想、分析、比较、归纳、概括来发现解题条件或结论或结论成立的条件，因而对考生的能力要求较高。具体来说有探索条件型——结论明确，需要探索发现使结论成立的条件的题目；探索结论型——给定条件，但无明确的结论或结论不惟一，而要探索发现与之相应的结论的题目；探索规律型——在一定的条件状态下，需探索发现有关数学对象所具有的规律性或不变性的题目；探索存在型——在一定的条件下，需探索发现某种数学关系是否存在的题目。

【范例讲析】：

例1 已知：△ABC和△DEF中，∠B=∠F=90°，AC=5，BC=3，DE=3，当EF=　　　 时，上述两个三角形相似。

【导析】：探索条件时要注意全面，类似于讨论；本题从结论着手，逆推其条件，解题过程类似于分析法。

例2 已知点M（p，q）在抛物线y=x²－1上，若以M为圆心的圆与x轴有两个交点A、B，且A、B两点的横坐标是关于x的方程x²－2px+q=0的两根。如图：

⑴当点M在抛物线上运动时，圆M在x轴上截得的弦长是否变化？为什么？

⑵若圆M与x轴的两个交点和抛物线的顶点C构成一个等腰三角形，试求p、q的值。

【导析】： 探索结论型题的特点是结论有多种可能，即它的结论是发散的；探索结论型题的一般解题思路是：①从特殊情形入手，发现一般性的结论；②在一般的情况下，证明猜想的正确性。

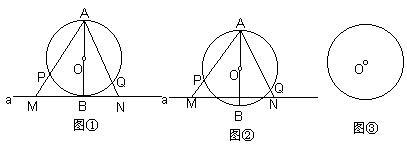
例3　　　　已知：AB是⊙O的直径，AP、AQ是⊙O的两条弦，如图①，过点B作⊙O的切线a，分别交直线AP、AQ于点M、N。可以得出结论AP·AM=AQ·AN成立。

⑴　　 若将直线a向上平行移动，使直线a与⊙O相交，如图②所示，其它条件不变，上述结论是否成立？若成立，写出证明；若不成立，说明理由；

⑵　　 若将直线a继续向上平行移动，使直线a与⊙O相离，其它条件不变，请在图③上画出符合条件的图形，上述结论成立吗？若成立，写出证明；若不成立，说明理由。

【导析】：本题特点是图形在运动或变化过程中，探索已知结论仍然成立。解这种探索规律型题的关键是抓住图形的本质特征，并仿照原题进行证明即可。

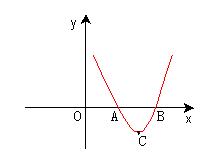
例4　　　　如图，二次函数y=x²－4x+3的图象与x轴交于A、B两点，顶点为C。

⑴求A、B、C三点的坐标；

⑵在y轴上求作一点P（不写作法）使得PA+PC最小，并求P点的坐标；

⑶在x轴上方的抛物线上，是否存在点Q，使得以A、B、Q三点为顶点的三角形与△ABC相似？如果存在，求出Q点的坐标；如果不存在，请说明不存在的理由。

【导析】：探索存在型题的结论只有两种可能：存在或不存在；存在型问题的解题步骤是：①假设存在；②推理得出结论（若得出矛盾，则结论不存在；若不得出矛盾，则结论存在）。