初三数学第二学期第二次质量检测
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页,满分120分,考试时间为120分钟.
第Ⅰ卷(选择题 共48分)
一、选择题(共12个小题,每小题4分,共48分)
在每个小题给出的四个备选答案中,只有一个是符合题目要求的,请将你认为符合题目要求的答案选出来.
1.-5的绝对值是( )
A.5 B.-5 C.±5 D.![]()
2.据测算,我国每年因沙漠化造成的直接经济损失超过万元,用科学记数法表示这个数,应记为( )
A.![]() 万元 B.
万元 B.![]() 万元
万元
C.![]() 万元 D.
万元 D.![]() 万元
万元
3.下列二次根式中属于最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.甲、乙两人在相同的情况下,各射靶10次,两人命中环数的平均数![]() ,方差
,方差![]() ,
,![]() ,则射击成绩较稳定的是( )
,则射击成绩较稳定的是( )
A.甲 B.乙 C.一样 D.不能确定
5.若∠A是锐角,且sinA=cosA,则∠A的度数是( )
A.30° B.45° C.60° D.90°
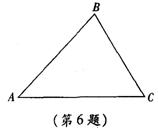
6.如图,到△ABC的三个顶点距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高线的交点 D.三条边的垂直平分线的交点
7.已知AB、CD是⊙O的两条直径,则四边形ABCD一定是( )
A.等腰梯形 B.菱形 C.矩形 D.正方形
8.函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≥-1 B.x>-1且x≠2
C.x≠2 D.x≥-1且x≠2
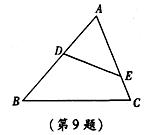
9.如图,在△ABC中,若∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为( )
A.![]() B.7 C.
B.7 C.![]() D.
D.![]()
10.下列说法:
①如果两个三角形的周长之比是![]() ,那么这两个三角形的面积之比是3∶4;
,那么这两个三角形的面积之比是3∶4;
②平行四边形是中心对称图形;
③经过三点有且只有一个圆;
④化简![]() 的结果是
的结果是![]() .
.
其中正确命题的个数是( )
A.4 B.3 C.2 D.1
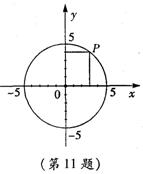
11.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y都是整数,则这样的点共有( )
A.4个 B.8个 C.12个 D.16个
12.一家三人(父亲、母亲、女儿)准备参加旅行团外出旅游,甲旅行社告知:“父母买全票价,女儿按半价优惠”,乙方旅行社告知:“家庭旅游可按团体票计价,即每人均按全票价的![]() 收费”,若这两家旅行社每人的全票价相同,则优惠条件是( )
收费”,若这两家旅行社每人的全票价相同,则优惠条件是( )
A.甲比乙更优惠 B.乙比甲更优惠
C.甲与乙优惠条件相同 D.与原票价有关
第Ⅱ卷(非选择题 共72分)
二、填空题(共4个小题,每小题4分,共16分)
13.化简:![]() __________________.
__________________.
14.若点(m,-m)在反比例函数![]() 的图象上,则k_______0(填“>”或“<”)
的图象上,则k_______0(填“>”或“<”)
15.已知两圆的半径分别是一元二次方程![]() 的两个根,若两圆的圆心距为5,则这两个圆的位置关系是__________.
的两个根,若两圆的圆心距为5,则这两个圆的位置关系是__________.
16.己知两个任意正数a和b,有下列命题:
(1)若a+b=2,则![]() ;
;
(2)若![]() ,则
,则![]() ;
;
(3)若![]() ,则
,则![]() .
.
根据以上三个命题所提供的规律,试猜想出a+b与![]() 应满足的最佳关系式:______________________;
应满足的最佳关系式:______________________;
三、解答题(共7个小题,共56分)
17.(本题满分9分)
(1)(5分)计算:![]()
(2)(4分)分解因式:![]()
18.(本题满分8分)
解不等式组: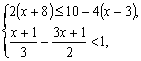 并求出其整数解.
并求出其整数解.
19.(本题满分7分)
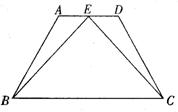
已知:如图,四边形ABCD是等腰梯形,AB=DC,AD∥BC,点E在AD上,且EB=EC,试问点E是AD的中点吗?若是,请给出证明,若不是,请说明理由.
20.(本题满分8分)
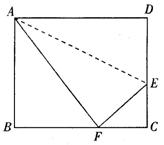
已知,如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,若折痕![]() ,且
,且![]() .
.
(1)证明:△AFB∽△FEC;
(2)求矩形ABCD的周长.
21.(本题满分8分)
对于上抛物体,在不计空气阻力的情况下,有如下关系式:![]() ,其中h(米)是上抛物体上升的高度,
,其中h(米)是上抛物体上升的高度,![]() (米/秒)是上抛物体的初速度,g(
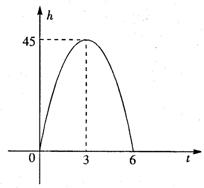
(米/秒)是上抛物体的初速度,g(![]() )是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.
)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.
(1)求:![]() 和g;
和g;
(2)几秒后,物体在离抛出点25米高的地方?
22.(本题满分8分)
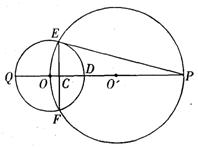
如图,⊙O'经过⊙O的圆心,E、F是两圆的交点,直线OO'交⊙O'于点P,交EF于点C,交⊙O于点Q,且![]() ,
,![]() .
.
(1)求证:PE是⊙O的切线;
(2)求⊙O和⊙O'的半径的长;
(3)若点A在劣弧![]() 上运动(与点Q、F不重合),连结PA交劣弧
上运动(与点Q、F不重合),连结PA交劣弧![]() 于点B,连结BC并延长交⊙O于点G,设CG=x,PA=y,求y关于x的函数关系式,并写出自变量x的取值范围.
于点B,连结BC并延长交⊙O于点G,设CG=x,PA=y,求y关于x的函数关系式,并写出自变量x的取值范围.
23.(本题满分8分)
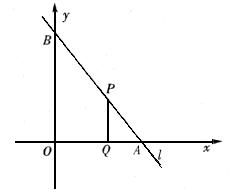
如图,直线![]() 与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程
与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程![]() 的两个根(OB>OA),P是直线
的两个根(OB>OA),P是直线![]() 上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q.
上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q.
(1)求tan∠BAO的值;
(2)若![]() 时,请确定点P在AB上的位置,并求出线段PQ的长;
时,请确定点P在AB上的位置,并求出线段PQ的长;
(3)当点P在线段AB上运动时,在y轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案
一、选择题(共12个小题,每小题4分,共48分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | D | B | B | D | C | D | C | D | C | B |
二、填空题(共4个小题,每个小题4分,共16分)
13.![]() ; 14.<; 15.相交; 16.
; 14.<; 15.相交; 16.![]() (或
(或![]() )
)
三、解答题(共7个小题,共56分)
17.(本题满分9分)
(1)(5分)计算:![]()
解:原式=![]() …………………………………………… 4分
…………………………………………… 4分
=5.…………………………………………………………………… 5分
(2)(4分)分解因式:![]()
解法1:原式=![]() …………………………………………… 1分
…………………………………………… 1分
=![]() …………………………………………… 2分
…………………………………………… 2分
=![]() ………………………………………………… 3分
………………………………………………… 3分
=(x-y)(x+y)(x-1) …………………………………… 4分
解法2:原式=![]() …………………………………………… 1分
…………………………………………… 1分
=![]() …………………………………………… 2分
…………………………………………… 2分
=![]() ………………………………………………… 3分
………………………………………………… 3分
=(x-1)(x+1)(x-y). …………………………………… 4分
18.(本题满分8分)
解:解不等式2(x+8)≤10-4(x-3),得
x≤1. ……………………………………………………………………… 2分
解不等式![]() ,得
,得
x>-1 ……………………………………………………………………… 4分
∴ 这个不等式组的解集为-1<x≤1. …………………………………………… 6分
∴ 这个不等式组的整数解为0,1. ……………………………………………… 8分
19.(本题满分7分)
解:点E是AD的中点. …………………………………………………………… 1分
证明:∵ AD∥BC,AB=CD,
∴ ∠ABC=∠DCB …………………………………………………………………… 2分
∵ EB=EC,
∴ ∠EBC=∠ECB …………………………………………………………………… 3分
∴ ∠ABE=∠DCE …………………………………………………………………… 4分
∴ △ABE≌△DCE. ………………………………………………………………… 6分
∴ AE=DE,即点E是AD的中点. ……………………………………………… 7分
20.(本题满分8分)
解(1)∵四边形ABCD是矩形,
∴ ∠B=∠C=∠D=90°. ………………………………………………………… 1分
由题意,得Rt△ADE≌Rt△AFE,
∴ ∠AFE=∠D=90°. ……………………………………………………………… 2分
∴ ∠AFB+∠EFC=90°,
又∵ ∠EFC+∠FEC=90°,
∴ ∠AFB=∠FEC. …………………………………………………………………… 3分
∴ △AFB∽△FEC. …………………………………………………………………… 4分
(2)由![]() ,可设EC=3k(k>0〕,则FC=4k.在Rt△ECF中,EF=5k.
,可设EC=3k(k>0〕,则FC=4k.在Rt△ECF中,EF=5k.
∴ DE=5k.
∴ DC=AB=8k. ……………………………………………………………………… 5分
又∵ △ABF∽△FCE,
∴ ![]() ,即
,即![]() ,
,
∴ BF=6k.
∴ AF=10k. ………………………………………………………………………… 6分
在Rt△AFE中,![]() ,
,
∴ ![]() ,
,
∴ k=1(cm)(取正值). …………………………………………………………… 7分
∴ 四边形ABCD的周长=2(AB+BC)=2(8+10)=36(cm) ………………… 8分
21.(本题满分8分)
解:(1)由图可知,![]() 的图像经过(6,0)、(3,45)点, … 1分
的图像经过(6,0)、(3,45)点, … 1分
∴ 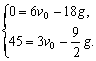 …………………………………………………………………… 3分
…………………………………………………………………… 3分
解这个方程组,得![]() ,g=10.
,g=10.
∴ ![]() (米/秒),g=10(
(米/秒),g=10(![]() ). ………………………………………… 4分
). ………………………………………… 4分
(2)由(1)得,函数关系式是![]() . …………………………………… 5分
. …………………………………… 5分
当h=25时,则![]() . …………………………………………………… 6分
. …………………………………………………… 6分
解这个方程,得![]() ,
,![]() . …………………………………………………… 7分
. …………………………………………………… 7分
∴ 经过1秒或5秒的物体在离抛出点25米高的地方. ………………………… 8分
22.(本题满分8分)
解:(1)连结OE.
∵ OP是⊙O'的直径,
∴ ∠OEP=90°,
∴ PE是⊙O的切线. ………………………………………………………………… 2分
(2)设⊙O、⊙O'的半径分别为r,r'.
∵ ⊙O与⊙O'交于E、F,
∴ EF⊥OO',![]() .
.
∴ 在Rt△EOC、Rt△POE中,∠OEC=∠OPE.
∴ sin∠OEC=sin∠OPE=![]() .
.
∴ ![]() .
.
即![]() , …………………………………………………………………………… 3分
, …………………………………………………………………………… 3分
∴ ![]() ,解得r=4.
,解得r=4.
Rt△OPE中,![]() .
.
∴ r'=8. …………………………………………………………………………… 4分
(3)连结OA.
∵ ∠OEP=90°,CE⊥OP,
∴ ![]() .
.
又∵ PE是⊙O的切线,
∴ ![]() ,
,
∴ PC·PO=PB·PA.
即 ![]() ………………………………………………………………………… 5分
………………………………………………………………………… 5分
又∵ ∠CPB=∠APO,
∴ △CPB∽△APO,
∴ ![]() ,
,
∴ ![]() .
.
由相交弦定理,得BC·CG=CF·CE,
∴ ![]() . ……………………………………………………………………… 7分
. ……………………………………………………………………… 7分
∴ PA=4CG,
即y=4x(![]() ). …………………………………………………………… 8分
). …………………………………………………………… 8分
23.(本题满分8分)
解:(1)由已知可得![]()
又∵ ![]() ,
,
∴ ![]() ,
,
即![]() .
.
∴ ![]() .
.
∴ AB=10或AB=-18(不合题意,舍去).
∴ AB=10, …………………………………………………………………………… 2分
∴ ![]() .
.
解得 ![]() ,
,![]() .
.
∵ OB>OA, ∴ OA=6,OB=8.
∴ ![]() ……………………………………………………………… 4分
……………………………………………………………… 4分
(2)∵ ![]() ,
,
∴ ![]() .
.
∵ PQ∥BO,
∴ △PQA∽△BOA.
∴![]() . 5分
. 5分
∴ ![]() . ∵ AB=10,
∴ AP=5.
. ∵ AB=10,
∴ AP=5.
又∵ ![]() , ∴
, ∴ ![]() .
.
∴ PQ=PA·sin∠BAO
![]() . …………………………………………………………………… 6分
. …………………………………………………………………… 6分
(3)存在
M点的坐标分别为![]() (0,0)、
(0,0)、![]() 、
、![]() . ……………………… 8分
. ……………………… 8分