初三数学第二学期期末质量抽查复习题
一、填空题
1.![]() 的相反数是______________ ,-2的倒数是_________
的相反数是______________ ,-2的倒数是_________
2.空气的体积质量是0.001239克/厘米3,用科学记数法表示,则为_______克/厘米3。
3.若分式![]() 的值为0,则
的值为0,则![]() =______
=______
4.当![]() 时,
时,![]() =_____________
=_____________
5.观察一列数的规律并填空:0,3,8,15,24,……则这列数的第2002个数是________
6.若![]() 的两根是
的两根是![]() ,则
,则![]() =__________
=__________
7.方程组![]() 的解是________
的解是________
8.小明用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,那么小明最多能买________支钢笔。
9.已知点P在第二象限,且到x轴的距离是2,到y轴的距离是3,则点P的坐标是______
10.抛物线![]() 的顶点坐标是________,开口方向是________,对称轴是___________。
的顶点坐标是________,开口方向是________,对称轴是___________。
11.为了了解用电量的多少,李明在六月初连续几天同一时刻观察电表显示的度数,记录如下:
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表显示(度) | 117 | 120 | 124 | 129 | 135 | 138 | 142 | 145 |
 估计:李明家六月份的总用电量是_______度
估计:李明家六月份的总用电量是_______度
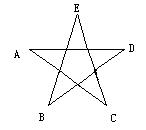
12.如图,我国国旗上的五角星图的每一个顶角都相等,其度数是______
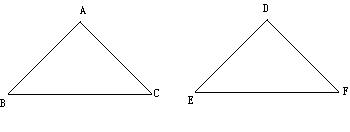
13.如图,在△ABC和△DEF中,已知AB=DE,要使△ABC≌△DEF,根据三角形全等的判定定理,还需添加条件(填上你认为正确的一种情况)______________
14.把边长为1的正方形对折n次后,所得图形的面积是_________
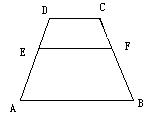 15.如图,在梯形ABCD中,AB∥CD AB=3,CD=1,则该梯形的中位线长为_____,若EF∥AB,且
15.如图,在梯形ABCD中,AB∥CD AB=3,CD=1,则该梯形的中位线长为_____,若EF∥AB,且![]() ,则EF的长为_________
,则EF的长为_________
 16.在△ABC中,点D、E分别在AB、AC上,DE∥BC,如果AD=8,DB=6,EC=9,那么AE=__________
16.在△ABC中,点D、E分别在AB、AC上,DE∥BC,如果AD=8,DB=6,EC=9,那么AE=__________
17.某中学升国旗时,小明同学站在离旗杆底部12m处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为45°,若他的双眼离地面1.3m,则旗杆高度为_______m。
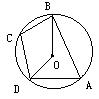
18.如图,在⊙O的内接四边形ABCD中,∠BCD=130°,则∠BPD的度数为________。
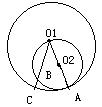 19.如图,⊙O1的半径O1A是⊙O2的直径,C是⊙O1上的一点,O1C交于⊙O2于点B,若⊙O1的半径等于5cm,
19.如图,⊙O1的半径O1A是⊙O2的直径,C是⊙O1上的一点,O1C交于⊙O2于点B,若⊙O1的半径等于5cm,![]() 的长等于⊙O1周长的
的长等于⊙O1周长的![]() ,则
,则![]() 的长是_______cm。
的长是_______cm。
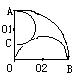 20.如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆O1和以OB为直径的半圆O2相切,则半圆O1的半径为_________。
20.如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆O1和以OB为直径的半圆O2相切,则半圆O1的半径为_________。
二、选择题
1.下列计算中,正确的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.将![]() 分解因式,结果是( )
分解因式,结果是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
3.已知![]() 为实数,且
为实数,且![]() ,那么
,那么![]() 的值为( )
的值为( )
(A)1 (B)-3或1 (C)3 (D)-1或3
4.一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件服装仍可获利15元,则这种服装每件的成本价是( )
(A)120元 (B)125元 (C)135元 (D)140元
5.函数![]() 中自变量
中自变量![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() 且
且![]() (D)
(D)![]() 且
且![]()
6.二次函数![]() 的最小值为( )
的最小值为( )
(A)-35 (B)-30 (C)-5 (D)20
7.无论m为何值,直线y=x+2m与y=-x+4的交点不可能在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
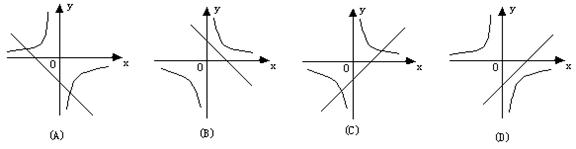 8.函数
8.函数![]() 与
与![]() (
(![]() )在同一坐标系中的大致图象可能是( )
)在同一坐标系中的大致图象可能是( )
9.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是![]() ,那么另一组数据3x1-2、3x2-2、3x3-2、3x4-2、3x5-2的平均数和方差分别是( )
,那么另一组数据3x1-2、3x2-2、3x3-2、3x4-2、3x5-2的平均数和方差分别是( )
(A)2,![]() (2)2,1 (3)4,
(2)2,1 (3)4,![]() (D)4,3
(D)4,3
10.在频率分布直方图中,各个小长方形的面积和等于( )
 (A)频数 (B)组数 (C)1 (D)方差
(A)频数 (B)组数 (C)1 (D)方差
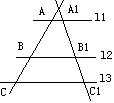
11.如图![]() ∥
∥![]() ∥
∥![]() 已知AB=6cm,BC=3cm,
已知AB=6cm,BC=3cm,
A1B1=4cm,则线段B1C1的长度为( )
(A)6cm(B)4cm(C)3cm(D)2cm
12.如果直角三角形的三条边长为2、4、a,那么a的取值可以有( )
(A)0个 (B)1个 (C)2个 (D)3个
13.已知梯形的下底长是5cm,它的中位线长是4cm,则它的上底长是( )
(A)2.5cm (B)3cm (C)3.5cm (D)4.5cm
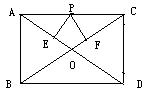 14.如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC,垂足为E,PF⊥BD,垂足为F,则PE+PF的值为( )
14.如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC,垂足为E,PF⊥BD,垂足为F,则PE+PF的值为( )
(A)![]() (B)2 (C)
(B)2 (C)![]() (D)
(D)![]()
15.四边形ABCD的对角线AC、BD交于点O,设有以下论断:(1)AB=BC;(2)∠DAB=90°;(3)BO=DO,OA=OC;(4)矩形ABCD;(5)菱形ABCD;(6)正方形ABCD,则在下列推论中不正确的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
16.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
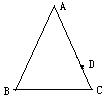 (A)16 (B)14 (C)16或14 (D)16或9
(A)16 (B)14 (C)16或14 (D)16或9
17.1m长的标杆直立在水平的地面上,它在阳光下的影长为0.8m,此时,若某电视塔的影长为100m,则此电视塔的高度应是( )
(A)80m (B)85m (C)120m (D)125m
18.如图,⊙O的直径为10,弦AB的长为8,
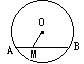 M是弦AB上的动点,则OM的长的取值范围
M是弦AB上的动点,则OM的长的取值范围
为( )
(A)3≤OM≤5 (B)4≤OM≤5
(C)3 < OM < 5 (D)4 < OM < 5
19.在△ABC中∠C=90°,AB=13,AC=12,以B点为圆心,以6为半径的圆与直线AC的位置关系是( )
(A)相切 (B)相交 (C)相离 (D)不确定
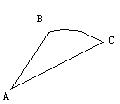 20.某工件形状如图所示,圆孤BC的度数为60°,AB=6cm,B点到C点的距离等于AB,∠BAC=30°则工件的面积等于( )
20.某工件形状如图所示,圆孤BC的度数为60°,AB=6cm,B点到C点的距离等于AB,∠BAC=30°则工件的面积等于( )
(A)4![]() cm2
(B)6
cm2
(B)6![]() cm2
cm2
(C)8![]() cm2
(D)10
cm2
(D)10![]() cm2
cm2
三、解答题
1.计算: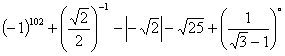
2.解方程组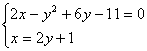
3.解不等式组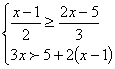 并写出不等式组的整数解。
并写出不等式组的整数解。
4.已知:二次函数![]() ,其中
,其中![]() 为实数。
为实数。
(1)求证不论![]() 取任何实数,这个二次函数的图象与
取任何实数,这个二次函数的图象与![]() 轴必有两个交点;
轴必有两个交点;
(2)设这个二次函数的图象与![]() 轴交于点A(x1,0)、B(x2,0),且x1,x2的倒数和为
轴交于点A(x1,0)、B(x2,0),且x1,x2的倒数和为![]() ,求这个二次函数的解析式。
,求这个二次函数的解析式。
5.A工人的5次操作技能测试成绩(单位:分)是:7、6、8、6、8;B工人这5次操作技能测试成绩的平均分![]() ,方差
,方差![]()
(1)求A工人操作技能测试成绩的平均分![]() 和方差
和方差![]() ;
;
(2)提出一个有关“比较A、B两工人的操作技能测试成绩”的问题,再作出解答。
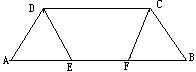 6.已知:如图,在梯形ABCD中,AB∥CD,E、F为AB上两点,且AE=BF,DE=CF,EF≠CD,求证:AD=BC
6.已知:如图,在梯形ABCD中,AB∥CD,E、F为AB上两点,且AE=BF,DE=CF,EF≠CD,求证:AD=BC
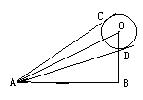
7.如图,天空有一气球O,某人在A处测得球心仰角∠OAB=30°,气球对A的视角∠CAD=2º,已知气球半径为1m,求球心O到地面的距离OB(精确到0.1m)
8.某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出,已知生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R、P与x的关系式分别为R=500+30x,P=170-2x。
(1)当日产量为多少时,每日获得的利润为1750元
(2)当日产量为多少时,可获得最大利润?最大利润是多少?
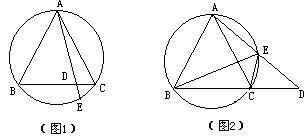
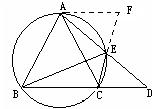
9.如图1,圆内接三角形ABC中,AB=AC,经过A点的弦与BC及![]() 分别相交于点D和E,则结论AB2=AE·AD是成立的。
分别相交于点D和E,则结论AB2=AE·AD是成立的。
(1)如果E点在△ABC的外接圆上移动,如移动到![]() (不与A、C重合)这时AE的延长线交BC的延长线于点D,请问:AB2=AE·AD仍然成立吗?如果你认为成立,请给出证明过程。
(不与A、C重合)这时AE的延长线交BC的延长线于点D,请问:AB2=AE·AD仍然成立吗?如果你认为成立,请给出证明过程。
(2)在图2中,连结CE、BE若∠BAC=60º,求证:BE=AE+CE
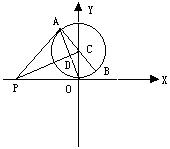
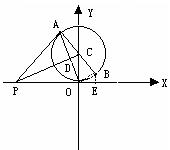
10.已知:如图,在直角坐标系中,以y轴上的点C为圆心,1为半径的圆与x轴相切于原点O,点P在x 轴的负半轴上,PA切⊙C于点A,AB为⊙C的直径,PC交OA于点D。
 (1)求证:PC⊥OA
(1)求证:PC⊥OA
(2)若点P的坐标为(-2,0),求直线AB的解析式。
(3)若点P在x轴的负半轴上运动:原题的其他条件不变,设点P的坐标为(x,0),四边形POCA的面积为S,求S与点P的横坐标x之间的函数关系式;
(4)在(3)的情况下,分析并判断是否存在这样的一点P,使S四边形POCA=S△AOB?若存在,直接写出点P的坐标(不写过程);若不存在,简要说明理由。
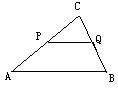 11.如图,已知:△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与点A、C不重合)。Q点在BC上。
11.如图,已知:△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与点A、C不重合)。Q点在BC上。
(1)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(2)试问:在AB上是否存在点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长。
参考答案
一、填空填
1.![]() ,
,![]() ;2.1.239×10-3;3.X=3;4.x-3;5.20022-1(或);6.-3;7.
;2.1.239×10-3;3.X=3;4.x-3;5.20022-1(或);6.-3;7.![]() ;8. 13;9.(-3,2);10.(1,2),向下,x=1;11. 120;12. 36º 13. 答案不惟一;14.
;8. 13;9.(-3,2);10.(1,2),向下,x=1;11. 120;12. 36º 13. 答案不惟一;14.![]() 15.2,
15.2,![]() 16.12;
17.13.3; 18. 100º; 19.
16.12;
17.13.3; 18. 100º; 19.![]() ; 20. 4
; 20. 4
二、选择题
1.B 2.D 3.A 4.B 5.C 6.B 7.C 8.D 9.D 10.C 11.D 12.C 13.B 14.A 15.C 16.D 17.D 18.A 19.B 20.B
三、解答题
1.解:原式=![]() =-3
=-3
2.解: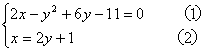
由(1)代入(2),得:![]()
![]()
∴![]()
把![]() 分别代入(2)得:
分别代入(2)得:
![]()
∴原方程的解为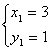 ,
,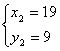
3.解得![]() ∴
∴![]() ∴整数解为x=4,5,6,7
∴整数解为x=4,5,6,7
4.(1)证:△=[-2(m-1)]2-4(m2-2m-3)
=4(m2-2m+1-m2+2m+3)
=16>0
∴不论m取何实数,这个二次函数的图象与x轴必有两个交点。
(2)由题知![]() 是方程
是方程![]() 的两个实数根。
的两个实数根。
∴![]()
![]()
∵![]() ∴
∴![]()
![]()
∴![]()
∴![]() 或
或 ![]()
5.解:(1)![]()
![]()
(2)如:“A、B两工人的操作技能测试的平均成绩谁好?”
∵![]()
∴A、B两位工人的操作技能测试的平均成绩一样好。
又如:“A、B两位工人的操作技能测试成绩谁更稳定?”
∵![]() ∴A工人的操作技能测试成绩更稳定。
∴A工人的操作技能测试成绩更稳定。
6.∵DC∥EF,EF≠CD ∴四边形CDEF是梯形
又∵DE=CF, ∴梯形CDEF是等腰梯形
∴∠DEF=∠CFE, ∴∠DEA=∠CFB
又∵AE=BF,DE=CF
∴△AED≌△BFC ∴AD=BC
7.连结OC,则OC⊥AC ∵AC、AD是⊙O的两条切线
∴∠CAO=∠DAO=![]() ∠CAD=1º
∠CAD=1º
在Rt△OAB中 ![]() ∠CAO=
∠CAO=![]()
∴![]()
在Rt△OAB中 ∠OAB=30º
∴![]() (米) 答:略。
(米) 答:略。
8.解:(1)根据题意得1750=px-R
(170-2x)x-(500+30x)=1750
∴x1=25 x2=45>40(舍去)
(2)px-R=-2x2+140x-500
=-2(x-35)2+1950
∴当x=35时,最大利润为1950元。
答:略
9.证(1)∵AB=AC
 ∴∠ABC=∠ACB=∠AEB
∴∠ABC=∠ACB=∠AEB
又∵∠BAE=∠DAB
∴△ABE∽△ADB
即![]() ∴AB2=AE·AD
∴AB2=AE·AD
(2)延长CE至F,使EF=AE连结AF
∵∠BAC=60º 又AB=AC
∴∠BAC=∠ABC=∠ACB=60º
∠AEF=180º-∠AEC
=180º-(∠AEB+∠BEC)
=180º-(∠ACB+∠BAC)
=60º
又∵EF=AE
∴∠EAF=60º
∴∠BAE=∠FAC=60º+∠CAE
 又∵∠ABE=∠ACF AB=AC
又∵∠ABE=∠ACF AB=AC
∴△BAE≌△CAF
∴BE=CF=CE+AE
10.(1)证:∵PA、PO是⊙C的切线
∴PA=PO
∴∠PAC=∠POC=90º AC=OC
∴△PAC≌△POC
∴∠APD=∠OPD
在等腰△PAO中,由∠APD=∠OPD得∠ADP=∠ODP=90º
∴PC⊥AO
(2)作BE⊥x轴于E
由△BOE∽△CPO得![]() 可求得B点坐标为(
可求得B点坐标为(![]() ) C(0,1)
) C(0,1)
设直线AB的解析式为y=kx+b
可解得y=-![]() x+1
x+1
(3)S四边形POCA=2S△POC 得:S=-x(x<0)
(4)若S四边形POCA=S△AOB
∴S四边形POCA=2S△AOC ∴CAOP= S△AOC
又∵OA⊥PC ∴PD=CD 可得四边形POCA为菱形 ∴PO=OC=1 ∴P(-1,0)
11.解(1)∵△PQC的周长与四边形PABQ的周长相等
∴PC+CQ=PA+AB+QB=![]() (△ABC的周长)=6
(△ABC的周长)=6
∵PQ∥AB ∴![]()
![]()
解得CP=![]()
(2) 1)据题意,如图a 当∠MPQ=90º PM=PQ时
由勾股定理逆定理 得∠C=90º
△ABC的AB边上的高为![]()
设PM=PQ=x由△CPQ∽△CAB 得 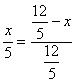
解得:![]() 即
即![]()
当∠MˊQP=90º QP=QMˊ时,同理可得![]()
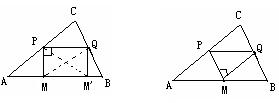 2)据题意,如图b,当∠PMQ=90º,MP=MQ时, 由等腰直角三解形得,M到PQ距离为
2)据题意,如图b,当∠PMQ=90º,MP=MQ时, 由等腰直角三解形得,M到PQ距离为![]() PQ , 设PQ=
PQ , 设PQ=![]() 由△CPQ∽△CAB 得
由△CPQ∽△CAB 得 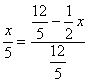 解得:
解得:![]() 即
即![]()
(a) (b)