初三（上）数学期末检测卷
一、选择题
1．在Rt△ABC中，∠C=90°, sinA=
, cosB=( )
A、
B、
C、
D、
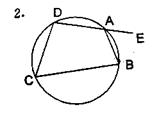
2．如图四边形ABCD内接于⊙O，E为DA延长线上一点，若∠BCD=45
，则∠BAE=（ ）
A、90° B、45°
C、60° D、135°
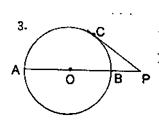3．如图，AB是⊙O的直径，P是AB延长线上的一点，PC切⊙O于点C，PC=3，PA=9，则PB=（ ）
A、3 B、8 C、9 D、1
4．自行车在同一平面内的两个圆形车轮的公切线的条线为（ ）
A、1条 B、2条 C、3条 D、4条
5．已知
、
满足+=5且为两根的一元二次方程是（ ）
A、x
－5x+6=0 B、x+5x+6=0
C、、x－5x－6=0 D、x+5x－6=0
6.函数y=
中自变量x的取值范围是（ ）
A、x>－5 B、x>－5或x≠0 C、x≥－5 D、x x≥－5且x≠0
7．如果反比例函数y=
的图象经过点P（－2，3），那么k的值是（ ）
A、－
B、－
C、－6
D、6
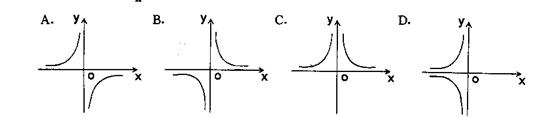
8．反比例函数y=－
的图象大致是（
）
9．抛物线y=(x+1) －1顶点坐标是（ ）
A、（1，－1） B、（－1，1） C、（1，1） D、（－1，－1）
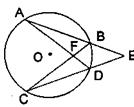10．如图，⊙O的弦AD、BC交于F，AB、CD延长线交于E，下列关系式中，正确的是（ ）
A、AB·BE=CD·DE B、AF·AD=CF·CB
C、AB·AE=CD·CE D、AF·DF=CF·BF
11．下列方程中，在实数范围内有解的是（ ）
A、2x+x+1=0 B、x－x－1=0
C、x－6x+10=0
D、x－
x+1=0
12．赵强同学借了一本书，共280页，要在两周借期内读完，当他读了一半时，发现平均每天要多读21页才能在借期内读完，他读前一半时，平均每天读多少页？如果设读前一半时，平均每天读x页，则下面所列方程中，正确的是（ ）
A、
+
=14 B、
+
=14
C、+
=14
D、
+
=1
13．直角坐标系中，两圆的圆心坐标分别是（
，0）和（0，1），它们的半径分别是3和5，则这两个圆的位置关系是（ ）
A、相离 B、相交 C、外切 D、内切
14．下列各图是在同一直角标系内，二次函数y=ax+(a+c)x+c与一次函数y=ax+c的大致图象，有且只有一个是正确的，正确的是（
）
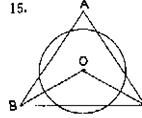
15．如图在△ABC中，∠A=70°，⊙O截△ABC的三边所得的弦长相等，则∠BOC=（ ）
A、125° B、135° C、130° D、140°
二、填空题
16．矩形的面积为2，一条边的长为x，另一条边的长为y，则用x表示y的函数解析式为__________________________（其中x>0）
17．在直角坐标系中，横坐标是正数、纵坐标是负数的点的点在第______象限
18．抛物线y=－x+x－4=0与y轴的交点坐标是___________
19．用换元法解方程（x－x）－5（x－x）+6=0，如果设x－x=y，那么原方程变为________
20．如图，已知AB、CD是⊙O的两条弦，OE、OF分别为AB、CD的弦心距，如果AB=CD，则可得出结论（至少填写两个）：___________________________________-
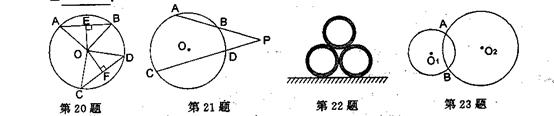
21．如图⊙O的弦AB、CD的延长线交圆外一点P，已知PB=4，AB=5，PD=3，则CD=___________
22．如图，施工工地的水平地面上，有三根外径都是1米的水泥管，两两相切地堆放在一起，则其最高点到地面的距离是______________（结果保留根号）
23．如图，⊙O
、⊙O
相交于点A、B，现给出4个命题
（1）若AC是⊙O的切线交⊙O于点C，AD是⊙O的切线且交⊙O于点D，则AB=BC·BD；
（2）连结AB、OO，若OA=15cm，OA=20cm，AB=24cm，则OO=25cm
（3）若CA是⊙O的直径，DA是⊙O的一条非直径的弦，且点D、B不重合，则C、B、D三点不在同一条直线上；
（4）若过点A作⊙O的切线交⊙O于点D，直线DB交⊙O于点C，直线CA交⊙O于点E，连结DE，则DE=DB·DC；则正确的命题是______________（只填序号）
一、计算与解答
24．2cos30°－sin90°－4cot30°+3tan60°
25.解方程: 
－
=1
x－y=1
26.解方程:
xy=12
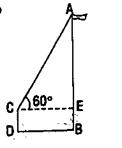27．如图，某同学用一个有60°角的直角三角板估测学校旗杆AB的高度，他将60°角的直角边水平放在1.5米高的支架CD上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D、B的距离为5米，求旗杆AB的高度。（精确到0.1米，取1.73）
四、
28．已知二次函数y=ax+bx的图象过点（2，0），（－1，6）
（1）求此二次函数的解析式
（2）在右边的直角坐标系中画出它的图象
（3）写出它的对称轴和顶点坐标
五、
29．一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这两种货车情况如表：
（1）求甲、乙两种货车每辆各能运货多少吨？
（2）现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货物，如果按每吨付运费30元计算，问：货主应付运费多少元？
| 第一次 | 第二次 | |
| 甲种货车辆数 | 2 | 5 |
| 乙种货车辆数 | 3 | 6 |
| 累计运货吨数 | 15.5 | 35 |
六、
30．如图，一次函数y=kx+b的图象与反比例函数y=
的图象交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式
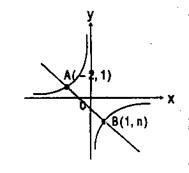（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围
七、
31．如图，已知⊙O、⊙O相交于A、B两点，且⊙O在⊙O上，过A作⊙O的切线AC交BO的延长线于点P，交⊙O于点C，BP交⊙O于点D，连结BC、AB
（1）求证：BC是⊙O的切线
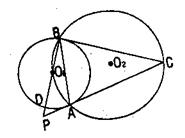（2）若PD=1，PA=
，求AC与AB的长
八、
32．已知：如图，P是⊙O的直径AB上的一个动点（P与A不重合），PD⊥AB，垂足为P，DC切⊙O于C，连结BC交PD于E，⊙O的半径为3，PD=7
（1）图a、图b、图c是点P由A向B运动过程中的三种情形。在图形的变化过程中△DCE的边、角或形状等存在多种规律，如：△DCE始终是锐角三角形；边CE逐渐增大；……请你通过观察、测量、比较，再写出两条与△DCE的边、角或形状等有关的规律。
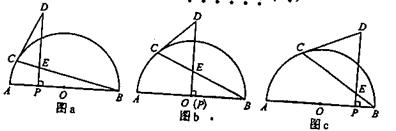（注意：可使用量角器、刻度尺等，找规律的过程中添加的字母或辅助线不能出现在结论中，不写推理过程，写出两条规律即可）
答：规律一：_____________________________________________________
规律二：________________________________________________________
(2)已知：当点P从A向B运动时，存在某一时刻，使∠D=60°，求此时AP的长。
九、
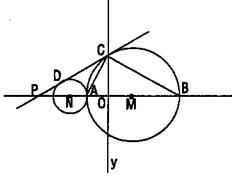
33．如图，已知P、A、B是x轴上的三点，点A的坐标为（－1，0）点B的坐标为（3，0），且PA：AB=1：2，以AB为直径画⊙M交y轴的正半轴于点C
（1）求P点的坐标
（2）求证：PC与⊙M相切
（3）在x轴上是否存在这样的点Q，使得直线QC与过A、C、B三点的抛物线只有一个交点？若存在，求点Q的坐标，若不存在，请说明理由。
（4）⊙N，使得圆心N在x轴的负半轴上，⊙N与⊙M外切，且与直线PC相切于D，问将过A、C、B三点的抛物线平移后，能否同时经过P、D、A三点？为什么？
34．在Rt△ABC中，∠ACB=90°，AB=2
，BC、AC分别是关于x的方程x－2(k+1)x+k+8=0的两根，求△ABC的内切圆的半径
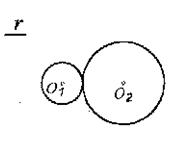35．已知：半径分别为r、2r的两圆⊙O、⊙O相外切
求作：⊙O
，使⊙O的半径为3r，且与⊙O、⊙O都相切（不写画法，保留作图痕迹）
36．某开发商对去年市场上一种商品销售数量及其销售利润情况进行了调查，发现：①销售数量y（万件）与时间x（月份）具有满足下表的一次函数关系
| 时间x（月份） | 1 | 2 | 3 | … | 12 |
| 销售数量y | 1.7 | 1.8 | 1.9 | … | 2.8 |
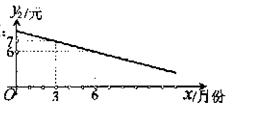②每一件的销售利润y（元）与时间x（月份）
具有如图所示的关系：请根据以信息解答下面问题：
（1）在三月份，销售这种商品可获利润多少万元？
（2）哪一个月的销售利润最大？请说明理由
参考答案
一、
ABDDA ACADD BCDDA
二、
16．Y=
17. 四
18．（0，－4）
19．y－5y+6=0
20. 略
21．9
22．（1+）米
23．①②③④
三、
24．原式=2·－1－4+3·
=－1
25. 5(x－1)－x=x(x－1)
x－5x+5=0
∴x=(5±)
检验知是原方程的根
26．（1）式代入（2）式整理行：y+y－12=0
∴y=3 y=4
x=4 x=－3
∴
y=3 y=－4
27.。解：在Rt△ACE中
AE=CE·tan60°=5=8.65
∴旗杆的高为：8.65+1.5≈10.2(米)
四、
28．（1）∵图象过点（2，0）（－1，6）
∴ 4a+2b=0
a－b=0
a=2
b=－4
∴y=2x－4x
(2)略
（3）对称轴x=1，顶点(1,－2)
五、
29．解：（1）设甲能运x吨，乙能运y吨
2x+3y=15.5
x=4
则 ∴
5x+6y=35 y=2.5
(2)应付运费：30(3x+5y)
=30×(3×4+5×)
=735(元)
六、30．解（1）由题意1=
∴m=－2
∴y=－
又n=
∴n=－2
1=－2k+b
k=－1
又∵ ∴得
n=k+b b=－1
∴y=－x－1
(2) x<－2或0<x<1
七、31．（1）连OA ∵AC是⊙O的切线
∴OA⊥AC 取∠OAC=90°
∴OC为⊙O的直径
∴∠CBO =90°
∴BC是⊙O的切线
（2）∵PC是⊙O的切线
∴PA=PD·PB
又∵PD=1 PA=
∴可求得PB=5
∴⊙O的半径为2
又∵PO·PB=PA·PC
∴可得PC=3
∴AC=2
连OC，OC为⊙O的直径
∴AB垂直OC，设AB交OC于H
由OC=
=
=2
∴AB=2BH=2·
=2·
=
32．规律一：△DCE始终是等腰三角形（或DC=DE，或∠DCE=∠DEC
规律二：∠CED逐渐减小（或∠DCE逐渐减小）
规律三：∠D逐渐增大
说明：括号内的看成是同一个规律
（2）连AC ∵∠D=60° ∴△DCE为等边三角形 ∴∠CED=∠DCE=CAB=60°
∴ 在Rt△ACB中，BC=AB·sin60°=9
又设PE=x， 则EB2x
PB=x
CE=9－2x
∴9－2x=7－x
DE=7－x
∴ x=2
∴PB=x
∴PA=4
33．（1）解：∵PA:AB=1:2 ∴PA=2 ∴P点坐标为（－3，0）
（2）连CM 在△COM和△PCM中， OM=1 CM=2 PM=4
=
由 ∴△COM～△PCM
∠CEO=∠PMC
∴∠PCM=∠COM=90° ∴PC与⊙M相切
（3）可求得过A、C、B三点的解析式为y=－(x+1)(x－3)
假设满足条件的点存在，坐标为Q（m,0）
设QC的解析式为：y=kx+b
=b
b=
则 ∴
km－b=0
k=－
∴QC的明析式为：y=－x+
∵QC与抛物线只有一个公共点， ∴方程－（x+1）(x－3)= －+只有等根
∴△=（2+
）=0 ∴m=－ ∴存在，且Q（－，0）（0，0）
（4）连DN，作DH⊥PN 设⊙N的半径为r
∵ND⊥PC ∴ND//MC ∴ND：MC=PN：PM
∴得r=
在Rt△PDN中，DH⊥PN
∵DN=NH·NP
即（）=NH·（2－）
∴得NH=
,
∴DH=
∴D坐标为（－2，）
∴将抛物线平移使其经过A、P两点的解析式为y=－(x+1)(x+3)
又验证，D点是该抛物线上的点。 ∴平移后，能同时过P、D、A三点
34.X=5－
35.五个圆
36．（1）13.3万元 （2）四月份