初三第二学期第一次数学月考试卷
（满分：150分 时间：120分）
姓名： 班组： 座号： 得分：
一、填空（每题3分，共39分）
|
1、函数y= 1 自变量X的取值范围是
2、函数y=2x2－1的对称轴是 ，开口方向 顶点坐标
3、直线y=－2x+1，经过 象限。
|
4、函数y= 1 当x<0时图象在 象限。
5、如果正比例函数y=3x和一次函数y=2x+K
的图象交点在等三象限，K的取值范围是 。
6、如图某宾馆的地面图案是用正方形和一种边长相等，但角不全相等的六边形材料铺成的，那么这种六边形的最大内角的度数是 。
7、已知一条弦分圆2：3的两部分则这条弦所对的圆周角度数是 。
8、二次函数y=mx2－3x+2m－m2的图象过原点则m=
9、已知：O为△ABC的内心，∠B=36°，则∠AOC=
10、△ABC中三边分别为6cm、8cm、10cm求内切圆半径 cm，外接圆半径
11、△ABC中，AB=AC=5cm、BC=6cm 内切圆的半径是
12、正六边形的半径是2cm，这个正六边形的边长是 cm.
13、⊙O1和⊙O2交于A、B两点，公共弦AB=6cm半径r1=4cm r2=5cmO1O2的长是 cm。
二、选择题（每题3分，共15分）
14、⊙O1和⊙O2处切，半径分别为2cm、6cm两公切线所夹锐角度数是（ ）
A、60° B、30° C、45° D、80°
15、半径为R的两个等圆相处切，与两圆都相切且半径为2R的圆有（ ）
A、2个 B、3个 C、4个 D、5个
16、两个边数相同的正多边形面积比是3：4，则它们的周长比是（ ）
A、3：4 B、3：2 C、9：16 D、4：3
17、在正三角形、正方形、正五边形、正六边形，其中共有（ ）个中心对称图形。
A、0个 B、1个 C、2个 D、4个
18、下列命题中正确的是（ ）
A、各内角都相等的圆内接多边形是正多边形
B、各边都相等的六边形是正六边形
C、正n边形的中心角与外角相等
D、正多边形是轴对称图形，也是中心对称图形
三、（共96分）
19、已知：如图⊙O，求作⊙O的内接正四边形（不写作法，保留作图痕迹）（8分）
·o
20、已知：两圆⊙O1与⊙O2相处切，且各内切于⊙O，△OO1O2的周长是18cm，求⊙O的半径R（8分）
21、（8分）已知弓形弦长2
3cm，弓形所在圆的半径为2cm，求这个弓形的高。
22、（8分）求半径为2cm的圆内接正方形的面积。
23、求同圆内接正三形与处切正三角形的面积比。（8分）
24、已知扇形弧长为10Лcm，面积为180Лcm2，求此扇形的圆心角和半径（8分）
25、已知矩形ABCD一边AB=10cm，另一边AD=4cm，求从直线AB为轴旋转一周所得圆柱表面积。（8分）
26、已知函数y=x2－(K+1)x+k，①K为何值时，图象的顶点在x轴，②K为何值时，图象的顶点在y轴上，③图象的顶点是否能在原点上，为什么？（8分）
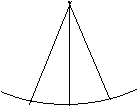
27、已知：如图⊙O的半径为R，∠AOB=60°⊙O1与⊙O内切,且与OA、OB都相切，求⊙O1的半径。（10分）
 |
|
|
|
28、二次函数y=－x2+(m－2)x+3(m+1)的图象与x轴交于A、B两点，C分别在y轴的两侧，与y轴交于点c，线段OA、OB长度的乘积等于6，①求m值。②连结AC、BC，求∠ACB的度数。（10分）
29、已知：如图P是⊙O的直径AB上的一个动点（P与A不重合垂直），PD⊥AB垂足为P，DC切⊙O于C连结BC交PD于E，⊙O的半径为3 3，PD=7，图（1）图（2）图（3）是点P由A向B运动过程中的三种情形，在图形的变化过程中△DCE的边、角或形状等存在多种规律。如：△DCE始终是锐角三角形，边CE逐渐增大。……请你通过观察、测量、比较，再写出两条与△DEC的边，角或、形状等有关的规律，（注意：可使用量角器，刻度尺等找规律的过程中添加字母或辅助线，不能出现在结论中，不写推理过程，写出两条规律即可）（12分）
D
D
C D
c E
C E
E
A P B A O B A P B
（1）答：规律一： 规律二：
（2）已知P点从A向B运动时，存在某一时刻，使∠D=60 ，求此时AP的长。