初三第一学期数学测验试卷
一、填空题：（2×18=36）（计算中有Л的保留Л）姓名_______班级_________
1、数
是精确到了位_______________；
2、如果一组数据a1、a2、a3、…an的方差是2，那么一组数据3a1、3a2、3a3、…3an的方差是 ；
3、三班为希望工程捐款，其中10名同学每人捐款15元，12名同学每人捐款20元，8名同学每人捐款25元，18名同学每人捐款30元，其中2名同学每人捐款50元，则该班同学捐款数目的中位数是_________元。
4、两圆相交，半径分别为3cm，4cm，圆心距为5cm，则公共弦长为 __ 。
5、已知实数a满足
那么
的值是_________；
6、一条弧的半径为15cm，长度为10πcm，则圆心角为________度。
7、计算：
=_______________；
8、一扇形对的弧的长度为36πcm，则圆心角为
度，则面积为_____cm；
9、数
中有无理数_个;
10、
数
，他们由大到小的顺序为____________；
11、
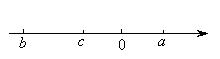一纳米为
米，则35纳米科学记数为__________________米；
12、实数
，
，
在数轴上的对应点如图所示，化简 
。
13、若、互为相反数，、
互为倒数，
绝对值为
，则
。
14、王大爷对自己的鱼塘中的鱼的总重量进行估计。第一次捞出100条，并将每条鱼作出记号放入水中；当它们安全混合于鱼群后，又捞出200条，称得重量为416千克，且带有记号的鱼有20条。王大爷的鱼群中估计共重 千克；
15、正六边形的边心距为
，则内切圆与外切圆所形成的圆环的面积为___________；
16、函数
与X轴的两个交点间的距离为_______________；
17、如图，两个同心圆，点A在大圆上，AXY为小圆的割线，
若AX·AY=8，则圆环的面积为 ______________ ；
18 Rt△ABC中，AB=5，BC=3将Rt△ABC绕着点C旋转60º，则点A所走的路程是______
二、选择：（每题3分共30分）
1、如果正三角形，正方形，正五边形，正六边形的周长相等，那么面积最大的是（ ）A）正三角形 B）正方形 C）正五边形 D）正六边形
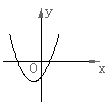
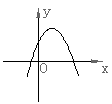
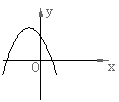
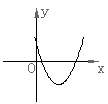2、二次函数
的图象大致为（ ）
A B C D
3、下列哪个是计数器不能直接算出的（ ）
A）平均数 B）方差
C）标准差 D）
4、下列哪个组合不能进行无缝镶嵌（ ） A正三角形和正方形
B正三角形和正六形 C正三角形和正八形 D正六角形和正方形
5、设是最小的自然数，是最大的负整数，是绝对值最小的有理数，则，，三数的和为( ) A．
B．
C．
D．不存在
6、下列命题中，①
的平方根是
②
的立方根是3 ③
④绝对值等于它本身数是0和1 ⑤倒数等于它本身数是0和1 ⑥平方根等于它本身数是0和1⑦立方根等于的实数是 ⑧
其中正确的有（ ）个
A ）1 B）2 C）3 D ） 4
7、某校有学生1200人，为测量平均身高，从中抽取一个班45人进行测量，则正确的是（ ） （A）总体是1200人 （B）样本是450人
（C）样本容量是45 （D）个体是每一个学生
8、方程
的解为（ ）
A）
B） 和2
C）3
D）
和3
9、正三角形的边心距与半径的比是（ ）.
（A）2：1 （B）1：2 （C）
：4
（D）：2
10、
、
与
的大小关系是( )
A）．
B）．
C）．
D）．
三、解答题
1、 如图，A为⊙O外一点，AO交⊙O于P，AB切⊙O于B，AP=5cm，
AB=
cm。求图中阴影部分的面积。6分
2、为了解某中学初中三年级男学生的身体发育情况，对男学生的身高进行了测量，下表是根据上述数据填写的频率分布表的一部分：
| 分 组 | 频数 | 频率 |
| 156.5~161.5 | 3 | A |
| 161.5~166.5 | B | 0.10 |
| 166.5~171.5 | 4 | 0.20 |
| 171.5~176.5 | C | 0.30 |
| 176.5~181.5 | 5 | D |
| 合 计 |
（1）请通过计算求ABCD的值 4分（2）画出频率分布图 3分
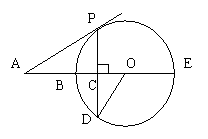3、如图，BE是⊙O的直径，点A在EB的延长线上，弦DP⊥BE于C，连结OD，且∠AOD = ∠APC（1）求证，AP是⊙O的切线；（2）若OC：CB = 1：2，且AB = 9，求⊙O的半径及sinA的值（3+6=9分）
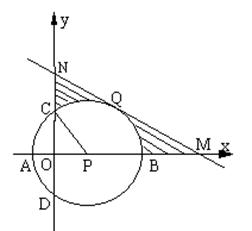
4、如图，在直角坐标系中，以x轴上一点P（1,0）为圆心的圆与x轴,y轴分别交于A、B、C、D四点，连结CP，cos∠APC＝1/2。 (1) 求⊙P的半径R；（2）若过弧CB的中点Q作⊙P的切线MN交x轴于M,交轴于N，求直线MN的解析式；（3）求图中阴影部分面积S；（4）一抛物线过A与B，且顶点在圆上，求抛物线的解析式（2+3+3+4=12分）
