初三第一学期数学期末考试

初三第一学期数学期末考试

一．填空题：（每小题3分，共30分）

1.如果反比例函数的图象经过点，则这个函数的解析式是　　　　　　　　　　　　  。

2.两圆半径分别为3和5，d表示这两圆的圆心距，当时，则这两圆的位置关系是　　　 。

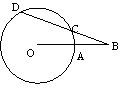3．一次函数y=x+2的图像与x轴、y轴围成三角形的面积S=　　　　  。

4．已知 y与x＋l成正比例，当x=5时,y＝12，

则y关于x的函数解析式是　　　　。

5.如图，B是⊙O外一点，BO交⊙O于点A，BCD是⊙O的割线，

若BA=3，BC=4，CD=5， 则⊙O的半径为　　　　　　 。　　　　　　　　　　 第5题

6.如果等边三角形边长为4，则由它的内切圆与外接圆组成的

圆环面积等于________。

7.如图ＡＤ∥ＢＣ，ＡＤ⊥ＢＥ，ＢＤ⊥ＣＤ，ＢＤ＝ＣＤ，

ＡＤ＝ＡＢ＝１，是以Ａ为圆心，ＡＢ为半径的圆弧，

是以Ｂ为圆心，ＢＤ为半径的圆弧．则阴影部分的面积Ｓ＝　　　　　　。　　  第7题

8.为圆心的三个圆两两外切，

则⊙A、⊙B、⊙C的半径分别为　　 　　　　　　　  　　。

9.已知两个圆是同心圆，大圆的弦AE、BE分别切小圆于C、D点，若, 则劣弧=　　 　度，劣弧=　　　　　　度；

10．正n边形的内角和等于它的一个外角的24倍，则n＝_______．

二．选择题：（每小题3分，共36分）

题号	11	12	13	14	15	16	17	18	19	20	21	22
答案

11.函数的自变量的取值范围是（　　　）

A．　　 B．　　  C．　　　 D．

12.圆的两弦相交，一弦长为4㎝，且被交点平分，另一弦被交点分成1：4，

则另一弦长是（　 　）

A．1㎝　　　 B．4㎝　　　　C．5㎝　　　　D．8㎝

13.如图，AB是⊙O的直径，∠ACD=15°，则∠BAD的度数为（　　　 ）　　　　

A、75°　　　　　　B、72°　　　　 C、70°　　　D、65°

14.给出下列函数：(1); (2);　(3)y=(x>0) ;(4)　　　 第13题

其中，y随x的增大而减小的函数是（　 　）

A、（1）、（2）.　B、（2）、（3）.　C、(3)、(4).　D 、（2）、（3）、（4）　　

15.下列命题中的假命题有（　　　 ）个

　　设两圆半径分别为R和r，圆心距为d，那么两圆相交；

　　‚如果两圆相切，那么切点一定在连心线上；

　　ƒ相交两圆的连心线垂直平分公共弦；

　　„两圆外切时，它们共有3条公切线。

　　A．1个　　　　　B．2个　　　　　C．3个　　　　　D．4个

16.当K＜0时，反比例函数y＝和一次函数y＝kx＋2的图象在图中的（　　　 ）

17.抛物线y＝x²－2x－1的顶点坐标是（　　　 ）

A.（1，－1）　　　 B.（－1，2）　　　 C.（－1，－2）　　  D.（1，－2）

18.已知两圆的半径分别是7和1，圆心距是8，那么这两圆公切线的长是（　　　　）

A、10　　　　　　　 B、　　　　　  C、　　　　D、7

19.若⊙O₁和⊙O₂相交于A、B两点，⊙O₁和⊙O₂的半径分别为2和，公共弦长为2，

　则的度数为（　　　）

　 A． 　　 B． 　　　C． 　　　 D．

20.关于二次函数y =ax²+bx+c的图象有下列命题：①当C=0时，函数的图象经过原点；②当C＞0且函数的图象开口向下时，ax²+bx+c=0必有两个不等实根；③函数图象最高点的纵坐标是；④当b=0时，函数的图象关于y轴对称。其中正确的个数是（　　　）

A.1个　　　　　 B、2个　　　 C、3个　　　　D. 4个

21.如图：MN是半圆的直径，若∠E＝20°，∠PMQ＝40°，则∠MQP＝（ 　　 ）。

（A）30°；（B）35°；（C）40°；（D）45°。

22.如图，正方形ABCD内接于⊙O,E为 DC的中点，

直线BE交⊙O于点F，若⊙O的半径为，　　　　　　　　　　　　　　　　　 第21题

则BF的长为　（　　　）

A、　　B、　　C、　　D、　　

三．解答题：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 第22题

23. （6分）已知一次函数的图象与反比例函数的图象相交，其中有一个交点的纵坐标为－4，求这两个函数的解析式。

24．根据所给的条件，求二次函数的解析式：（8分）

（1）　　　 抛物线的顶点是（2，-1），并且经过点（-1，2）；

（2）　　　 函数的最小值是–3，并且图象与轴交点的横坐标分别是2和3。

五．证明题：

25．（5分）已知：如图，⊙O₁与⊙O₂相交于A、B两点，过A的直线与两圆分别交于C、D，⊙O₂的弦BD与⊙O₁交于E，CE的延长线与⊙O₂交于F。求证：DF²=DE·DB

26.（7分）如图（1）⊙O₁和⊙O₂外切于点A，BC是两圆的公切线，B、C为切点。

①求证：AB⊥AC

②当⊙O₁向左运动，⊙O₂向右运动到如图（2）的位置时，BC仍为两圆的公切线，O₁O₂交⊙O₁于点A，交⊙O₂于点D，BA、CD的延长线相交于点E，请判断EB与EC是否垂直，证明你的结论。

③当⊙O₁向右运动，⊙O₂向左运动到如图（3）的位置时，两圆相交于A、D两点，BC仍为两圆的公切线，若∠BDC=46°，试求∠BAC的度数。

六、解答题：

27.（5分） 已知抛物线y=ax²+bx+c经过A（－1,0）、B（3,0）、C（0,3）三点，

（1）　　　 求抛物线的解析式和顶点M的坐标，并在给定的直角坐标系中画出这条抛物线。

（2）　　　 若点（x₀,y₀）在抛物线上，且0≤x₀≤4,试写出y₀的取值范围。

（3）　　　 设平行于y轴的直线x=t交线段BM于点P（点P能与点M重合，不能与点B重合）交x轴于点Q，四边形AQPC的面积为S。

①　　 求S关于t的函数关系式以及自变量t的取值范围；

②　　 求S取得最大值时点P的坐标；

③　　 设四边形OBMC 的面积S^/,判断是否存在点P，使得S＝S^/ ,若存在，求出点P的坐标；若不存在，请说明理由。

29.（3分） 已知二次函数，它的图象与x轴只有一个交点，交点为A，与y轴交于点B，且AB=2。

　　(1)求二次函数解析式；

　　(2)当b<0时，过A的直线y=x＋m与二次函数的图象交于点C，在线段BC上依次取D、E两点，若，试确定ÐDAE的度数，并写出求解过程。

参考答案

一、填空题：

1.y=　　  2.相交　　 3.4　　　4. y=2x+2　　　 5. 4　　  6.4　  7.1　　

8. 2cm ,4cm , 3cm　　　  9.112　　124　　　 10. 8

二、选择题

1.D　 2.C　 3.A　 4.B　　5.A　 6.B　 7.D　 8.B　 9.B　 10.C　 11.B　 12.C　

三、解答题

23. 解：由题意得

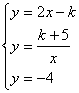　　　 ∴k=1

∴一次函数的解析式为y=2x－1　　 反比例函数解析式为y=

24.(1)由题意假设此抛物线解析式为y=a(x－2)²－1

∴a(－1－2)²－1=2　  　 

∴a=

∴此抛物线解析式为y=

(2)由题意设此抛物线解析式为y=a(x－2)(x－3),(a>0)

∴y=a(x²－5x+6)=a(x－)²－

∵函数最小值为－3，∴－

∴此抛物线解析式为y=12x²－60x+72

25.证明：连结AF、BF、AB

∠DBF对　∠DBF=∠DAF

∠DAP对　 同理∠C=∠ABD=∠AFD　　∠DFC=∠DBF　  △DFE∽△DBF

∠DAF=∠C+∠AFC　　　　　  ∠BDF=∠FDB

　　　　　  ∠CFD=∠AFC+∠AFD

26．

①证明：作两圆的内公切线交BC于点P

PA切⊙O_­1于点A　 PB=PA

PB切⊙O₁于点B　　　　　　　  　 

　　　　　　 同理PA=PC　　　　△ABC中

②EB⊥EC

③∠BAC=134°

27．解（1）由题意设此抛物线解析式为y=a₁(x+1)(x－3)

∴a₁(0+1)(0－3)=3,∴a₁=－1,∴此抛物线解析式为y=－x²+2x+3

∴y=－(x²－2x－3)=－(x－1)²+4　 ∴顶点M的坐标为（1，4）

（2）∵当x₀=4时，y₀=－16+8+3=－5，而由图象可知，y₀≤4

∴－5≤y₀≤4

(3)不存在这样的点P

29．∠DAE=45°