初三上学期几何期中考试

初三上学期几何期中考试

一、填空题：（每小题3分，共30分）

1．已知∠A+∠B=90°，sinA=，则cosB=　　　　 。

2．若α、β为锐解，且tanα=cotβ，则α+β=　　　 。

3．已知α、β、γ都是锐角，且sinα=，tanβ=，cotγ=1,则=　　　

4．一气球在离地面55米的上空，此时一观测器测得它的仰角为30°，则观测器与气球间的距离是　　　　 。

5．在Rt△ABC中，∠C=90°，如果sin(90°－A)=，那么cot(90°－A)=　　　 ，tanB=

　　　　.

6．在ΘO中，AB是直径，弦BC等于半径，则∠ABC=　　　 。

7．已知　P为半径是5cm的ΘO内一点，PO=3cm，则过P的最长的弦长为　　　 cm，最短的弦长为　　　cm。

8．在ΘO中，AB=120° ，则AB所含的圆周角为　　　 。

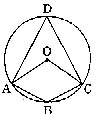
9．如图，四边形ABCD内接于ΘO，且∠AOC=100°，则∠D=　　　，∠B=　　　。

10．设圆内接正方形的边长为a，此正方形的面积与圆的面积之比为　　　　　 。

二、选择题：（每小题3分，共27分）

1．在直角三角形中，各边的长都扩大到原来的2倍，那么锐角A的余弦值（　　）

A．都扩大两倍　　  B．都缩小到一半　　 C．没有变化　　 D．不能确定

2．在△ABC中，已知sinA·cosB=0，那么这个三角形是（　　）三角形。

A．直角　　  B．锐角　　　C．钝角　　　 D．不能确定

3．△ABC中，∠A+∠B+∠C=180°，那么tan=(　　)

A．90°－C　　　B．cot　　　　C．tan　　 D．cot

4．在解直角三角形时，除直角外，知道其余5个元素中的（　　），就可以求出其余的未知数。

A．2个元素　　　　　　　　　　 B．至少有一个边和其它1个元素

C．至少有一个角和其它1个元素　 D．以上都不对

5．若A、B都是锐角，且tan+，则A、B分别是（　　）

A．60°，60°　　　B．30°，30°　　 C．30°，60°　　 D．60°，30°

6．如果由点A测得点B在北偏东15°的方向，那么由点B测得点A的方向为（　　）

A．北偏东15°　　　B．北偏西75°　　 C．南偏西15°　　D．南偏东75°

7．下列命题中正确的是（　　）

A．圆的对称轴就是直径　　　　　　  B．经过圆内定点的直径有无数条

C．经过圆上定点的弦只有一条　　　　D．经过圆心的弦是直径

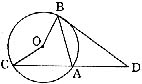8．如图，AB、AC为ΘO的两条弦，延长CA到D，使AD=AB，若∠ADB=30°，则∠BOC等于（　　）

A．60°　　　 B．120°

C．135°　　　D．150°

9．在两个等圆中，弦AB和CD的弦心距为d和d₁，若AB<CD，则d和d₁的关系是（　　 ）

A．d>d　　  B．d<d₁　　　C．d=d₁　　　D．不能确定

三、计算下列各题：（每小题5分，共15分）

1．2sin60°+　　　　　  2．

3．4cos30°－cos²20°－sin²20°－tan40°·tan50°

四、解答证明题：（每小题7分，共28分）

1．如图，已知：AB是ΘO的直径，弦CD⊥AB，M为AC上一点，延长AM、DC交于N。

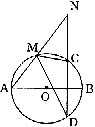求证：∠AMD=∠NMC

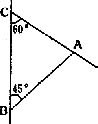
2．已知如图，C城市在B城市的正北方，两城市相距100千米，计划在两城市间修筑一条高速公路（即线段BC），经测量，森林保护区A在B城市的北偏东45°的方向上，又在B处，C城市的南偏东60°的方向上，已知森林保护区A的范围是以A为圆心，半径为50千米的圆？问：计划修筑的这条高速公路会不会穿越保护区？为什么？（）

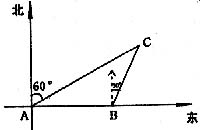
3．一轮船向东航行，在A处测得某岛C在北偏东60°的方向上，船前进8海里后到达再测C岛在北偏东30°的方向上，问船再前进多少海里便与C岛最近，最近距离是多少？

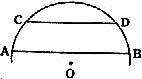
4．1998年的一场大洪水摧毁了无数的村庄、田园、屋舍，却不能摧垮全国人民抗洪的意志和决心。解放军某部尖刀连奉命赶往某地增援，途径一圆弧形拱桥，如图，上午8点测得水面AB宽32米，下午4点水面上升了4米，水面CD宽24米，当上游洪水按此速度上涨，增援部队最晚于几时前通过该桥？

初三上学期几何期中考试答案

一、填空题（每小题3分，共30分）

1.3/7　　2.90°　　3.90°　　 4.110米　　　5.5/12　　12/5　　　 6.60°　　 7.10

8.8.120°　　  9.50°　130°　　10.2:π

二、选择题（每小题3分，共27分）

1.C　　 2.A　　　3.D　　　4.B　　　5.D　　　6.C　　 7.D　　　 8.B　　　9.A

三、计算下列各题（每小题5分，共15分）

1．2　　　 2.　　  3.2－2

四、解答证明题（每小题7分，共28分）

1．证明：连结AD………………………………2分

∵A、D、C、M四点共圆　∴∠NMC=∠ADC……………………4分

∵AB⊥CD，AB是直径　∴AMC=AD　∴∠AMD=∠ADC……………6分

∴∠AMD=∠NMC…………………………………………7分

2．解：这条高速公路不会穿越保护区…………………………1分

过点A作AD⊥BC，垂足为D………………………………2分

在Rt△ADC中，CD=AD/tan60°　 在Rt△ABD中，BD=AD/tan45°……4分

根据题意，得AD/tan60°+AD/tan45°=100

∴AD=63.397>50…………6分

∴计划修筑的这条高速公路不会穿越森林保护区。………………7分

3．解：作CD⊥AB与AB延长线交于点D，D点为船与C岛最近距离……2分

由题意可知∠CAD=30°∠BCD=30°∠CBD=60°

∴∠ACB=∠CAD=30°　∴BC=AB=8……………………4分

在Rtt△CBD中BD=1/2BC=4　CD=4 …………………………6分

答：船再前进4海里便与C岛最近，最近距离是4海里。……7分

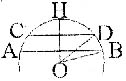4．解：过O作半径OH⊥AB于E，则OH垂直CD

于F，连结OB　OD，由垂径定理，得

BE=1/2AB=16　 DF=1/2CD=12…………2分

设OE=x　　ΘO半径为R，则OF=x+4

于是得， x²+16²=R²　　　　　　　　　　　 x=12

　　　  (x+4)²+12²=R²　　　　  　　　解得　R=20

∴FH=OH－OF=20－12－4=4米…………5分

上午8点到下午4点经过8小时，水面涨4米，当FH=4米时，再过8小时即午夜12点，洪水将漫过桥面，所以增援部队最晚应在12点前通过该桥。7分