初三上学期数学--解直角三角形单元检测题（A）
满分：100分；考试时间：90分钟
姓名： 学号： 成绩：
一、填空题：（每空1分，共20分）
1、旗杆的上一段BC被风吹断，顶端着地与地面成300角，顶端着地处B与旗杆底端相距4米，则原旗杆高为_________米。
2、在Rt△ABC中，∠ACB＝900，CD⊥AB于D，BC＝7，BD＝5，则sinB＝ ，cosA＝ ，sinA＝ ，tanA＝ ，cotA＝ 。
3、在△ABC中，∠ACB＝900，CD⊥AB于D，若AC＝4，BD＝
，则sinA＝ ，tanB＝
。
4、若
为锐角，cot＝
，则sin＝
，cos＝
。
5、查正弦表得
＝0.9650，则
＝ ；若
对应的修正值为0.0002，则
＝
；若
对应的修正值为0.0004，且cosA＝0.9646，则A＝
。
6、计算：（1）
＝
；
（2）
＝
。
7、计算：
＝
。
8、当
＝
时，
无意义。（00＜＜900）
9、在△ABC中，∠C＝900，若sinA＞cosA，则∠A的取值范围是 。
10、已知△ABC中，AB＝
，∠B＝450，∠C＝600，AH⊥BC于H，则AH＝ ；CH＝
。
二、选择题：（每小题2分，共20分）
11、已知cotA＝
，求锐角A（ ）
A、320 B、300 C、600 D、500
12、在Rt△ABC中，如果一条直角边和斜边的长度都缩小至原来的
，那么锐角A的各个三角函数值（ ）
A、都缩小 B、都不变 C、都扩大5倍 D、无法确定
13、若是锐角，且
，则为（ ）
A、540 B、360 C、300 D、600
14、在△ABC中，∠C＝900，CD是AB边上的高，则CD∶CB等于（ ）
A、sinA B、cosA C、tanA D、cotA
15、在△ABC中，∠C＝900，CD⊥AB于D，∠ACD＝，若tan＝
，则sinB＝（ ）
A、
B、
C、
D、
16、A、B、C是△ABC的三个内角，则
等于（ ）
A、
B、
C、
D、
17、若00＜∠A＜900，且
，则
的值为（ ）
A、5
B、
C、
D、
18、化简
的结果是（ ）
A、
B、
C、
D、
19、在Rt△ABC中，∠C＝900，
，则
∶
∶
为（ ）
A、2∶
∶ B、2∶∶3 C、2∶3∶
D、1∶2∶3
20、在△ABC中，若AB＝AC，则sinB等于（ ）
A、
B、
C、
D、
三、计算下列各题：（每小题5分，共10分）
21、
22、
四、解答下列各题：（每小题8分，共40分）
23、已知如图：AB∥DC，∠D＝900，BC＝
，AB＝4，
＝
，求梯形ABCD的面积。
24、方程
有实数根，求锐角的取值范围。
25、已知，如图：正方形ABCD中，E、F是AD上的两点，EF＝3，
＝
，
＝
，求FD的长。
26、已知△ABC中，∠A、∠B、∠C的对边分别是、、 (＞)，关于的方程
有两个相等的实数根。若∠A、∠B的余弦是关于的方程
的两个根。且△ABC的周长为24。
（1）试判定△ABC的形状，并证明你的结论；
（2）试求△ABC最大边的长度。
27、今年入夏以来，松花江哈尔滨段水位不断下降，达到历史最低水位。一条船在松花江某水段自西向东沿直线航行，如图，在A处测得航标C在北偏东600方向上。前进100米到达B处，又测得航标C在北偏东450方向上。在以航标C为圆心，120米长为半径的圆形区域内有浅滩。如果这条船继续前进，是否有被浅滩阻碍的危险？（供考生参考的数据：≈1.732）
五、知识运用：（10分）
28、为了测量校园内办公楼前一棵不可攀的树的高度，初三·六班数学兴趣小组做了如下的探索：
实践一：根据《物理》教科书中光的反射定律，利用一面镜子和一根皮尺，设计如图1的测量方案：把镜子放在离树8.7米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里能看到树梢顶点A，再用皮尺量得DE＝2.9米，观测者身高CD＝1.6米，请你计算树AB的高度（精确到0.1米）
实践二：提供选用的测量工具有：①皮尺一根；② 教学用三角板一副； ③高度为1.5米的测角仪（能测量仰角和俯角的仪器）一架，请用你所学的解直角三角形的有关知识，设计出求树高的方案，根据你所设计的测量方案，回答下面问题：
（1）在你设计的方案中，选用的测量工具是（填序号） ；
（2）在图2中画出你的设计方案和测量示意图；
（3）你需要测量的数据和角度分别用、、、
、、
、
表示；
（4）写出求树高的表达式：AB＝ 。
参考答案
一、填空题：
1、
；2、
，，
，
，
；3、
，；4、，
；
5、0.9650，0.9652，
；6、0，1；7、；8、450；9、450＜A＜900；10、4，
二、选择题：BBBBC，ABBBB
三、计算下列各题：
21、
22、
四、解答下列各题：
23、解：过B作BE⊥DC于E，∵tanC＝
∴设BE＝
，则EC＝
在Rt△BEC中，由勾股定理得：
即
解得：＝1
∴BE＝1，EC＝3
∴
＝
＝
24、解：∵方程有实数根
∴△＝
≥0
即
≤
∴00＜＜300
25、解：∵ABCD是正方形
∴∠FBC＝∠AFB
∴tan∠FBC＝tan∠AFB＝
＝
设AB＝
，则AF＝
又∵tan∠ABE＝
＝
＝
∴AE＝
又∵AF－AE＝EF＝3
∴－＝3
∴＝1
∴AF＝5，AB＝AD＝8
∴FD＝AD－AF＝3
26、（1）△ABC是直角三角形。
证明：∵方程有两个相等的实数根
∴△＝
＝0
∴
∴△ABC是直角三角形。
（2）由韦达定理得：
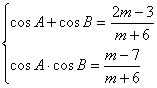
又∵A＋B＝900
∴
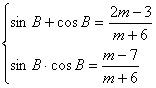
①平方并把②代入得：
整理得：
＝3，
＝19
当
＝3时，因
＝
＜1不符题意，故舍去。
∴＝19
此时原方程为：
＝，
＝
又∵＞
∴
设＝
，那么＝，＝
∵
＝24
∴
＝24
解得＝2
∴△ABC的最长边（斜边）：＝
＝10
27、解：过C作CD⊥AB的延长线于D
由题意知：∠CAD＝300，∠CBD＝450，AB＝100米
在Rt△ADC中有：AD＝
，即AD＝
①
在Rt△BDC中有：BD＝
，即BD＝
②
①－②得：AD－BD＝
即100＝
∴CD＝
＝
≈136.6（米）
∵CD＞120米
∴如果这条船继续前进，没有被浅滩阻碍的危险。
28、实践一：由光的反射定律知：∠AEB＝∠CED
又∵∠CDE＝∠B＝900
∴△CDE∽△ABE
∴
即
∴AB＝4.8米
答：这棵树高4.8米。
实践二：（1）①③
（2）如下图所示的两个方案
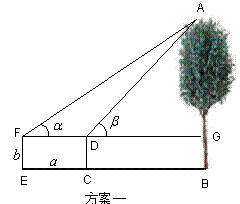
方案一：AB＝
方案二：AB＝
注：只要求考生设计出一种测量方案。