数学单元测试题[解直角三角形]
一. 选择题:(3´×12=36´)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
1.当锐角A>300时,sinA的值为______
A.小于
B.大于
C. 小于
D. 大于
2.下列等式成立的是_______
A.
B.
C.
D.
3.在
中,如果各边的长度同时扩大2倍,那么锐角A的正弦值和余弦值______
A.都扩大2倍 B.都缩小2倍 C.都不变 D.不能确定
4.在中,AB=AC,AB=2BC,那么sinB=_______
A.
B.
C.
D.
5. 在中,
:
:
=1:2:3,那么sinA:sinB:sinC=_________
A.1:2:3 B.1:
:2
C.
:
:
D.1:
:
6.已知α为锐角且
,则α的度数为_______
A.
B.
C.
D.
7.
的值等于________
A.2 B.0 C.2 D.1
8.下式成立的是________
A.
B.
C.
D.
9.若A、B、C为任意三角形的三个内角,下列各式能成立的是______
A.
B.
C.
D.
10.边长为a的等边三角形的面积为________
A.
B.
C.
D.
11.在中,
,如果
,那么
的值为________
A.
B.
C.
D.
12.一般情况下,测量楼高的最佳方法是_______
A.站在楼顶望地面两点，测得这两点的俯角,再量得这两点的距离，进行计算.
B.在地面上任取两点，测得这两点向上望的仰角,再测得这两点的距离，进行计算.
C.在地面上选适当的一点，使它与楼顶的仰角为300,再测量该点到楼底的距离，利用特殊值进行计算.
D.在地面上选适当的一点，使它与楼顶的仰角为450,只需测量该点到楼底的距离便求出楼高.
二.填空题:(2´×10=20´)
13.已知
,则
=__________,
=_________.
14.已知
,则cosA=_________,tanA=___________.
15.已知tanB·tan360=1,则锐角B=_________.
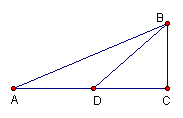
16.已知:如图, RtΔABC中
,则BC=_________.
17.已知等边三角形的两边分别为4㎝,5㎝,则此等腰三角形底角的正切值为__________.
18.在RtΔABC中,
b+c=6,则b=_________.
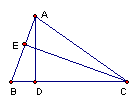19.如图,△ABC中,AD⊥BC于D,CE⊥AB于E，且BE＝2AE，已知AD＝
, tan∠BCE＝
，那么CE＝
.
20.化简:
=________________
三.计算题:(5´×4=20´)
21.求值：
+2sin30°－tan60°＋cot450
22. 计算：
23. 计算：
24. 计算：
+ 
四.解答下列各题:(6´×4=24´)
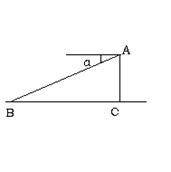23、如图，一飞机于空中A处探测到地面目标C，此时飞行高度AC=1300米，从飞机上看地平面控制点B的俯角α=17°，求飞机A到控制点B的距离？（精确到0.1米，参考数据：
sin17°=0.29，cos17°=0.96，tg17°=0.31，ctg17°=3.3）
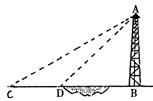
23.如图，河对岸有铁塔AB．在C处测得塔顶A的仰角为30°，向塔前进14米到达D，在D处测得A的仰角为45°，求铁塔AB的高．
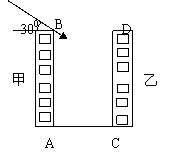20、下图为住宅区内的两幢楼，它们的高AB=CD=30m，现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求：
1）若两楼间的距离AC=24m时，甲楼的影子，落在乙楼上有多高？
2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
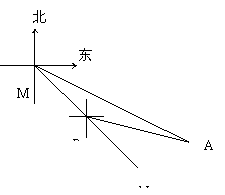7、金阳新开发区供水工程设计从M到N的一段的路线图如图所示，测得N点位于M点南偏东30º，A点位于M点南偏东60º，以A点为中心，半径为500m的圆形区域为文物保护区，又在B点测得BA的方向为南偏东75º，量得MB＝400m，请计算后回答：输水路线是否会穿过文物保护区？