数学高中阶段学校招生考试试卷1
（考试时间为90分钟，满分为120分）
一、选择题（每小题3分，共15分。每小题给出的4个选项中只有一个是正确的，请将所选选项的字母写在题目后面的括号内）
1、下列运算正确的是（ ）
（A）
（B）－0.005＝5×
（C）
（D）
2、如图1，某个反比例函数的图像经过点P，则它的解析式（ ）
（A）
（
＞0）
（B）
（＞0）
（C）（＜0
（D）（＜0
3、下列说法中正确的是（ ）
（A）有两边和其中一边的对角对应相等的两个三角形全等
（B）等腰三角形是轴对称图形，也是中心对称图形
（C）对角线互相平分的四边形是平行四边形
（D）有两边平行的四边形是梯形
4、关于的方程
的根是3，则
的值为（ ）
（A）4 （B）－4 （C）5 （D）－5
5、如图2，正方形的边长为，以各边为直径在正方形内画半圆，所围成的图形（阴影部分）的面积为（ ）
（A）
（B）2 （C）
（D）
二、填空题（每小题4分，共20分。请把正确答实填写在横线上）
6、若∠A是锐角，cosA＝
，则∠A＝
。
7、不等式组
的解集为
。
8、当
，
时，代数式
的值等于
。
9、如图3，AB是⊙O的直径，弦CD⊥AB，垂足为P，若AP∶PB＝1∶4。CD＝8，则AB＝ 。
10、与点 P（3，4）关于
轴对称的点的坐标为
；与点Q（－3，4）关于原点对称的点的坐标为
。
三、解答下列各题（每小题6分，共30分）
11、先化简后求值：
，其中
。
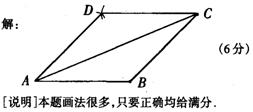
12、如图4，AB、AC分别是菱形ABCD的一条边和一条对角线，请用尺规把这个菱形补充完整。（保留作图痕迹，不要求写作法和证明）
13、如图5，灯塔A周围1000米水域内有礁石，一舰艇由西向东航行，在O处测得灯塔A在北偏东74°方向线上，这时O、A相距4200米，如果不改变航向，此舰艇是否有触礁的危险？（指定数学课使用科学计算器的地区的考生须使用计算器计算。以下数据供计算器未进入考场的地区的考生选用：cos740＝0.2756，sin740＝0.9613，cot740＝0.2867，tan740＝3.487）
14、在公式
中，已知
、
、
。求。
15、某商场出售某种文具，每件可盈利2元，为了支援贫困山区，现在按原售价的7折出售给一山区学校，结果每件盈利0.2元（盈利＝售价－进货价）。问该文具每件的进货价是多少元？
四、（每小题7分，共28分）
16、已知二次函数
的图像经过A（0，1），B（2，－1）两点。
（1）求和
的值；
（2）试判断点P（－1，2）是否在此函数图像上？
17. 为了了解中学生的身体发育情况，对某一中学同年龄的50名女学生的身高进行了测量，结果如下（单位：厘米）：
165 155 160 166 157 171 151 163 161 167
150 153 156 167 165 164 163 164 161 161
150 153 156 167 165 164 163 164 161 161
148 160 155 165 155 164 159 153 156 156
164 162 156 162 157 162 165 151 163 157
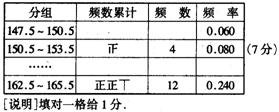
完成下面的频率分布表：
| 分 组 | 频数累计 | 频数 | 频率 |
| 147.5 ~ 150.5 |
| 3 | |
| 150.5 ~ 153.5 | |||
| 153.5 ~ 156.5 |
| 9 | 0.180 |
| 156.5 ~ 159.5 |
| 5 | 0.100 |
| 159.5 ~ 162.5 |
| 10 | 0.200 |
| 162.5 ~ 165.5 | |||
| 165.5 ~ 168.5 |
| 4 | 0.080 |
| 168.5 ~ 171.5 |
| 3 | 0.060 |
| 合 计 | 50 | 1.000 |
18、已知
、
为方程
的两根，且+＝6，
，求
和
的值。
19、如图6，在梯形ABCD中，AD∥BC，AD＝AB＝DC，BD⊥DC，求∠C的度数。
五、（每小题9分，共27分）
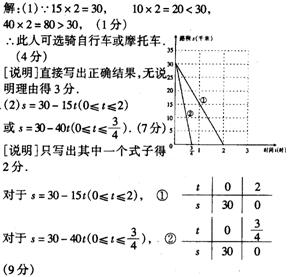
20、某人从A城出发，前往离A城30千米的B城。现在有三种车供他选择：①自行车，其速度为15千米/时；②三轮车，其速度为10千米/时；③摩托车，其速度为40千米／小时。
（1）用哪些车能使他从A城到达B城的时间不超过2小时，请说明理由。
（2）设此人在行进途中离B城的路程为s千米，行进时间为小时，就（1）所选定的方案，试写出s与t的函数关系式（注明自变量t的取值范围），并在图7所给的平面直角坐标系中画出此函数的图像。
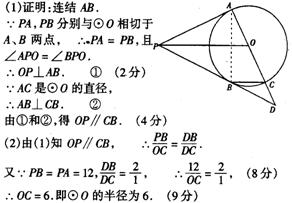
21、如图8：PA和PB分别与⊙O相切于A、B两点，作直径AC，并延长交PB于点D。连结OP，CB。
（1）求证：OP∥CB；
（2）若PA＝12，DB∶DC＝2∶1，求⊙O的半径。
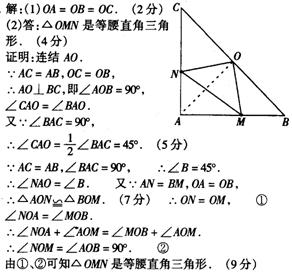
22、如图9：在Rt△ABC中，AB＝AC，∠BAC＝90°，O为BC的中点。
（1）写出点O到△ABC的三个顶点 A、B、C距离之部的关系；
（2）如果点M、N分别在线段AB、AC上移动，移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。
答案
11.
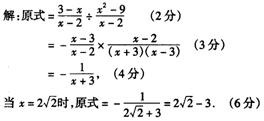
12.
13.
14.
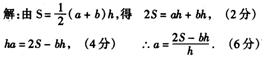
15.
16.
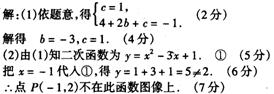
17.
18.
19.
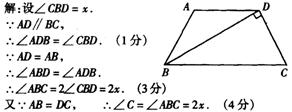
20.
21.
22.
