中考适应性考试数学试题
第I卷(选择题 共60分)
一、选择题(本大题共14个小题,在每个小题给出的四个选项中,只有一个选项是正确的,请把正确的选项选出来.第1~10小题每题4分,第11~14小题每题5分,共60分.选错、不选或选出的答案超出一个,均记0分.)
1.下列算式,正确的是( ).
(A)![]() (B)
(B)![]() ·
·![]()
(C)![]() (D)
(D)![]()
2.在下列各组根式中,是同类二次根式的是( ).
(A)![]() 和
和![]() (B)
(B)![]() 和
和![]()
(C)![]() 和
和![]() (D)
(D)![]() 和
和![]()
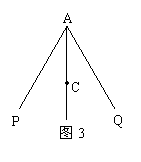
 3.如图1,AB∥CD,AC⊥BC,图中与∠CAB互余的角有( ).
3.如图1,AB∥CD,AC⊥BC,图中与∠CAB互余的角有( ).
(A)1个 (B)2个
(C)3个 (D)4个
4.把![]() 分解因式的结果是( ).
分解因式的结果是( ).
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
 5.如图2,天平右边托盘里的每个砝码的质量都是1千克,则图中显示物体质量的范围是( ).
5.如图2,天平右边托盘里的每个砝码的质量都是1千克,则图中显示物体质量的范围是( ).
(A)大于2千克 (B)小于3千克
 (C)大于2千克且小于3千克
(C)大于2千克且小于3千克
(D)大于2千克或小于3千克
6.如图3,已知AC平分∠PAQ,点B、B′分别在边AP、AQ上.下列条件中不能推出AB=AB′的是( ).
(A)BB′⊥AC (B)BC=B′C
(C)∠ACB=∠ACB′ (D)∠BAC=∠A B′C
7.某种T恤衫的进价为400元,出售时标价为600元,由于换季商店准备打折销售,但要保持利润不低于5%,那么至多打( ).
(A)6折 (B) 7折 (C) 8折 (D) 9折
8.剪纸是中国的民间艺术. 剪纸方法很多,图4是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案):
 |
图4
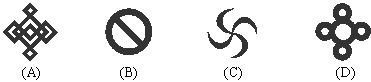 图5中的四个图案,不能用上述方法剪出的是
(
).
图5中的四个图案,不能用上述方法剪出的是
(
).
图5
9.被称为“神州1”的计算机运算速度为384 000 000 000次,保留四个有效数字,用科学记数法表示为( ).
(A)3.84×1011 (B)3.840×1011
 (C)3.84×1012
(D)3.840×1012
(C)3.84×1012
(D)3.840×1012
10.如图6,AB、AC与⊙O相切于B、C,∠A=50O,点P是圆上异于B、C的一动点,则∠BPC的度数是( ).
(A)65O (B)115O
(C)65O 和115O (D)130O 和50O
11. 如图7所示,函数y = kx + 1与函数![]() 在同一坐标系中的大致图象是( ).
在同一坐标系中的大致图象是( ).
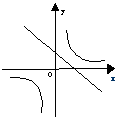
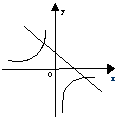
![]()


![]() (A) (B) (C) (D)
(A) (B) (C) (D)
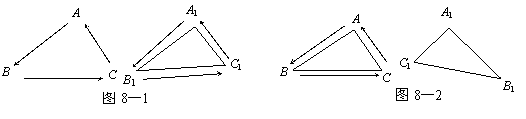 12.全等三角形又叫做合同三角形.
平面内的合同三角形分为真正合同三角形与镜面合同三角形. 假设△ABC和△A1B1C1是全等(合同)三角形, 且点A与点A1对应,点B与点B1对应,点C与点C1对应. 当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图8—1);若运动方向相反,则称它们是镜面合同三角形(如图8—2).
12.全等三角形又叫做合同三角形.
平面内的合同三角形分为真正合同三角形与镜面合同三角形. 假设△ABC和△A1B1C1是全等(合同)三角形, 且点A与点A1对应,点B与点B1对应,点C与点C1对应. 当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图8—1);若运动方向相反,则称它们是镜面合同三角形(如图8—2).
 | |||
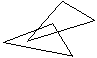
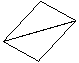
![]()
 两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180˚. 图9中的各组合同三角形,是镜面合同三角形的是( ).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180˚. 图9中的各组合同三角形,是镜面合同三角形的是( ).
图9
13.如图10所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A、B、C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ).
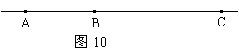
(A)点A (B)点B (C)A、B之间 (D)B、C之间
 14.图11—(1)是一个水平摆放的小正方体木块,图11—(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( ).
14.图11—(1)是一个水平摆放的小正方体木块,图11—(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( ).
图11
(A)25 (B)66 (C) 91 (D)120
第II卷(非选择题 共90分)
二、填空题(本大题共5个小题,每小题4分,共20分.只要求写最后结果)
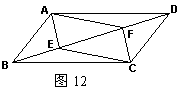 15.某银行设立大学生助学贷款,6年期的贷款年利率为6%,贷款利息的50%由国家财政贴补.某大学生预计6年后能一次性偿还2万元,则他现在可以贷款的数额是 万元.
15.某银行设立大学生助学贷款,6年期的贷款年利率为6%,贷款利息的50%由国家财政贴补.某大学生预计6年后能一次性偿还2万元,则他现在可以贷款的数额是 万元.
16.如图12,BD是平行四边形ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需要增加的一个条件是 (填上你认为正确的一个即可,不必考虑所有可能情形).
17.计算![]() 的结果为
.
的结果为
.
18.如果ab≠1且有5a2+2004a+9=0及9b2+2004b+5=0,那么![]() 的值是
.
的值是
.
 19.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图13所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm,则铁环的半径是
cm.
19.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图13所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm,则铁环的半径是
cm.
三、解答题(本大题共8个小题,共70分.解答应写出文字说明、证明过程或步骤)
20.(本题6分)先将![]() 化简,然后自选一个合适的x值,代入化简后的式子求值.
化简,然后自选一个合适的x值,代入化简后的式子求值.
21.(本题8分)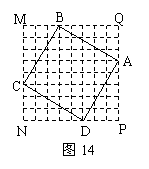 如图14,正方形MNPQ网格中,每个小正方形的边长都相等,正方形ABCD的顶点分别在正方形MNPQ的4条边的小方格顶点上.
如图14,正方形MNPQ网格中,每个小正方形的边长都相等,正方形ABCD的顶点分别在正方形MNPQ的4条边的小方格顶点上.
(1)设正方形MNPQ网格中每个小正方形的边长为1,求ΔABQ的面积和正方形ABCD的面积;
(2)设MB=a,BQ=b,利用这个图形中直角三角形和正方形的面积关系,你能验证已学过的哪一个数学公式或定理?相信你能写出简明的推理过程.
22.(本题8分)光明中学在一次健康知识竞赛活动中,抽取了一部分同学测试的成绩为样本,绘制的成绩统计图如下(图15),请结合统计图回答下列问题:
 (1)本次测试中,抽样的学生有多少人?
(1)本次测试中,抽样的学生有多少人?
(2)分数在90.5~100.5这一组的频率是多少?
(3)这次测试成绩的众数落在哪个小组内?
(4)若这次测试成绩80分以上(含80分)为优秀,则优秀率不低于多少?
23.(本题8分)2003年聊城“江北水城文化旅游节”期间,某单位组织36名员工拟租乘汽车赴聊城观光旅游.可租用的汽车有两种:一种每辆可乘8人,另一种每辆可乘4人,要求租用的车子不留空座,也不超载.
(1)请你给出不同的租车方案(至少三种);
 (2)若8个座位的车子的租金是300元/天,4个座位的车子的租金是200元/天,请你设计出费用最少的租车方案,并说明理由.
(2)若8个座位的车子的租金是300元/天,4个座位的车子的租金是200元/天,请你设计出费用最少的租车方案,并说明理由.
24.(本题8分)为了测得聊城铁塔的的高度,小明在离铁塔10米处的点C测得塔顶A的仰角为α ,小亮在离铁塔25米处的点D测得塔顶A的仰角为β(如图16),恰巧α+β=90˚.小明和小亮很快求出了铁塔AB的高度.你知道他俩是怎样求出来的吗?请写出你的解题过程(结果精确到0.01米).
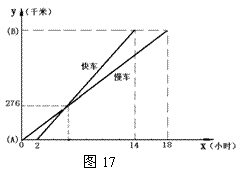 25.(本题10分)一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图17所示.请你根据图象,回答下列问题:
25.(本题10分)一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图17所示.请你根据图象,回答下列问题:
(1)慢车比快车早出发______小时,快车追上慢车时行驶了______千米,快车比慢车早________小时到达B地;
(2)在下列3个问题中任选一题求解(多做不加分).
①快车追上慢车需几个小时?
②求慢车、快车的速度.
③求A、B两地之间的路程.
26.(本题10分)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.如图18所示的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
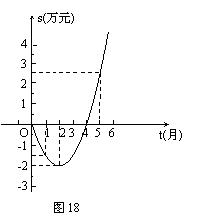 根据图象提供的信息,解答下列问题:
根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
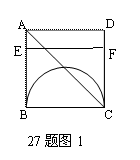
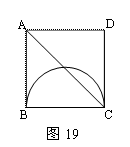 27.(本题12分)如图19,正方形ABED中,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A—D—C以2cm/s的速度向点C运动,设点E离开点B的时间为t(秒).
27.(本题12分)如图19,正方形ABED中,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A—D—C以2cm/s的速度向点C运动,设点E离开点B的时间为t(秒).
(1)当t为何值时,线段EF与BC平行?
(2)设1<t<2,当t为何值时,EF与半圆相切? (3)1≤t<2时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP∶PC的值.
参考答案
一、选择题(本大题共14个小题,在每个小题给出的四个选项中,只有一个选项是正确的,请把正确的选项选出来.第1~10小题每题4分,第11~14小题每题5分,共60分.选错、不选或选出的答案超出一个,均记0分.)
1.D; 2.B; 3.C; 4.B ; 5.C; 6.B; 7.B; 8.C; 9.B; 10.C; 11.B; 12.C; 13.A; 14.C.
二、填空题(本大题共5个小题,每小题4分,共20分.只要求写最后结果)
15.1.7; 16.DF=BE(不唯一); 17.2 ; 18.![]() ; 19.
; 19.![]() .
.
三、解答题(本大题共8个小题,共70分.解答应写出文字说明、证明过程或步骤)
20.(本题6分)
解:原式=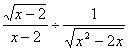
![]() …………………………………………………2分
…………………………………………………2分
=![]()
![]() …………………………………………………4分
…………………………………………………4分
取x=4,原式=2. …………………………………………………6分
注:x应在x>2的范围内取值,否则求值这一步不能得分.
21.(本题8分)
(1)∵网格中每个小正方形的边长为1,
有图可知AQ=3,BQ=4,∠Q=Rt∠,
∴SΔABQ=![]() AQ·BQ=6;同理SΔBCM=
SΔCDN= SΔADP=6.………………2分
AQ·BQ=6;同理SΔBCM=
SΔCDN= SΔADP=6.………………2分
又∵MQ=7,∴S正方形MNPQ=49.
∴S正方形ABCD= S正方形MNPQ -4 SΔABQ= 49-4×6=25. ……………………4分
(2)勾股定理或完全平方公式或平方差公式. ………………………5分
(只要给出其一即可得1分)
验证:在ΔBCM、ΔABQ中,
∵∠M=∠Q=∠ABC= Rt∠,∴∠MBC=∠QAB.
又∵AB=BC,∴ΔBCM≌ΔABQ.
同理ΔCDN≌ΔDAP≌ΔBCM. ……………………………………………6分
∵MB=a,BQ=b,S正方形MNPQ= S正方形ABCD+4 SΔABQ,
∴![]() ,
,
即![]() (完全平方公式).…………………………8分
(完全平方公式).…………………………8分
或
又∵S正方形ABCD=S正方形MNPQ -4 SΔABQ,
∴AB2=![]() ,即AB2=
,即AB2=![]() .
.
设AB=c,得c 2=![]() (勾股定理). ……………………………………8分
(勾股定理). ……………………………………8分
22.(本题8分)
(1)2+3+4+41=50(人) ………………………………2分
(2)![]() =
=![]() =0.08 ……………………………………4分
=0.08 ……………………………………4分
(3)众数落在80.5~90.5这一小组内 ……………………………………6分
(4)这次测试成绩的优秀率不低于90%。 ……………………………………8分
23.(本题8分)(1)方案1:四辆8人车,一辆4人车 4×8+1×4=36
方案2:三辆8人车,三辆4人车 3×8+3×4=36
方案3:二辆8人车,五辆4人车 2×8+5×4=36
方案4:一辆8人车,七辆4人车 1×8+7×4=36
方案5:九辆4人车 9×4=36
(只要写出三个方即可得3分)
(2)设8座车x辆,4座车y辆,则费用w=300x+200y.……… 5分
∵8x+4y=36,且0≤8x≤36,0≤x≤![]() ,
,
∴w=1800-100x. …………………………………………… 6分
∴当x取最大整数值,即x=4时,w的值最小.
故最佳方案为四辆8人车,一辆4人车. …………………………… 8分
注:如果用文字说明,只要叙述合理可分步给分.
24.(本题8分)
解:在RtΔABC中,AB=10tgα;
在RtΔABD中,AB=25tgβ;………………………………………………………3分
∵α+β=90˚,∴AB=25tg(90˚-α)=25ctgα,
∴AB2=10tgα·25 ctgα=250.…………………………………………………………5分
∴AB=![]() (米). ………………………………………7分
(米). ………………………………………7分
答:铁塔的高度为15.81米. ……………………………………………………8分
注:本题也可以用相似三角形来解.
25.(本题10分)解:(1)2,276,4. (每空1分,共3分)
(2)设快车追上慢车时,慢车行驶了x小时,则慢车的速度可以表示为![]() 千米/小时,快车的速度为
千米/小时,快车的速度为![]() 千米/小时,根据两车行驶的路程相等,可以列出方程
千米/小时,根据两车行驶的路程相等,可以列出方程
![]() ,解得x=6(小时).
,解得x=6(小时).
所以,①快车追上慢车需6-2=4(小时);
②慢车的速度为![]() 千米/小时,快车的速度为
千米/小时,快车的速度为![]() 千米/小时;
千米/小时;
③A、B两地间的路程为46×18=828千米. …………………………………10分
其他解法,酌情给分.
26.(本题10分)解:(1)设s与t的函数关系式为s=at2+bt+c
由题意得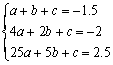 (或
(或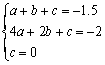 )
)
解得![]()
∴s=![]() ··································································································· 4分
··································································································· 4分
(2)把s=30代入s=![]()
得30=![]()
解得t1=10,t2= -6(舍)
答:截止到10月末公司累积利润可达到30万元·············································· 7分
(3)把t=7代入,得
s=![]()
把t=8代入,得
s=![]()
16-10.5=5.5
答:第8个月公司获利润5.5万元.…………………………………………10分
 27.(本题12分)
27.(本题12分)
解:(1)设E、F出发后运动了t秒时,有EF∥BC(如图1)则
BE=t,CF=4-2t,即有t=4-2t,t=![]() .
.
∴当t为![]() 秒时,线段EF与BC平行.
秒时,线段EF与BC平行.
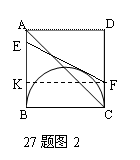 (2) 设E、F出发后运动了t秒时,EF与半
(2) 设E、F出发后运动了t秒时,EF与半
圆相切(如图2),过F点作KF∥BC交AB于K,则
BE=t,CF=4-2t,EK= t-(4-2t)=3 t -4,
EF=EB+FC= t+(4-2t)= 4-t .
又∵EF2=EK2+FK2,∴![]() .
.
即![]() .
.
∵1<t<2,∴![]() .
.
∴当t为![]() 秒时,EF与半圆相切. …………………………………………8分
秒时,EF与半圆相切. …………………………………………8分
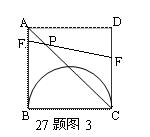 (3)当1≤t<2时,E、F出发后运动了t秒时,EF位置如图3所示,则
(3)当1≤t<2时,E、F出发后运动了t秒时,EF位置如图3所示,则
BE=t,AE=2-t,CF=4-2t,
∴![]() .
.
又∵AB∥DC,∴△AEP∽△CFP . ∴![]() .
.
即点P位置与t的取值无关 .
∴当1≤t<2时,点P的位置不会发生变化,且AP∶PC的值为![]() .……………12分
.……………12分