初中毕业升学数学模拟试题（一）
班级 姓名 学号 得分 I卷 II卷
I 卷
一、填空题：（每小题3分，共45分）
（1）
的倒数是 ；
（2）2000年全国第五次人口普查结果我国大陆人口约人，用科学技术法表示为 ；
（3）9的平方根是 ；
（4）不等式组
的解集是 ；
（5）分解因式：
；
（6）计算：tg32
tg58= ；
（7）点P（
，
）在第三象限，那么点M（
，
）在第 象限；
（8）函数
的自变量x的取值范围是 ；
（9）等腰直角三角形斜边上的高为1 cm，它的一条直角边长 ；
（10）若两个相似三角形的相似比为
，则这两个相似三角形的高的比为
；
（11）当
时，直线
不经过第 象限；
（12）半径为12 cm，圆心角为120的扇形面积为 ；E
F
（13）一个半径为5 cm，它的一条弦长为8 cm，
D C
则弦心距是 ；
（14）于数据组2，4，4，5，3，9，4，5，1，8，
G H
其众数、中位数、分别是 ； A B
（15）如右图，长方体中，与棱AB平行的面是 ；
二、选择题（每小题3分，共12分）
（16）代数式
的值是8，那么代数式
的值为--------------------（ ）
A 1 B 2 C 3 D 4
（17）下列命题中正确的是---------------------------------------------------------------------------（ ）
A 对角线互相垂直平分的四边形是矩形 B 圆内接平行四边形一定是正方形
C 菱形既是轴对称图形又是中心对称图形 D 一组对边平行的四边形是梯形
（18）（1）在下列二次根式
中，最简二次根式的个数有----（ ）
A 1 个 B 2 个 C 3 个 D 4 个
（19）若关于x的方程
有两个不相等的实数根，则k的取值范围--（ ）
A k ≥0 B k ＞ 0 C k ＞ - 1 D k≥ 1
三、解答题：
（20）化简求值：
，其中
（10分）
（21）已知，如图，在平行四边形ABCD中，E是AD的中点，延长CE交BA的延长线于点F，求证：AB = AF（10分）
F
A
E
D
B C
（22）为了了解中学生的体能情况，某校抽取了50名初三学生进行一分钟跳绳次数测试，将数据整理后，画出部分频率分布直方图，已知图中从左到右前四个小组的频率分别为：
0.04、0.12、0.4、0.28，根据已知条件求：
① 
第四小组的频数是多少？（3分）
 |
次数
149.5 159.5 169.5 179.5 189.5 199.5
② 第五小组的频率是多少？（3分）
③ 在这次测试中，跳绳次数的中位数大约落在哪一个小组？（2分）
④ 请补全频率分布直方图：（2分 ）
（23）如图，梯形ABCD内接于⊙O，AD∥BC，过B引⊙O的切线分别交DA、CA的延长线于E、F；①求证：
；②已知 
，求
的长；（13 分）
F
E
A
D
O
B
C
II 卷
一、填空题：（每小题3分，共6分）
（1）已知
和
为一元二次方程
的两个实数根，并且 和满足不等式
，则实数
的取值范围是
；
（2）在一次如图，在梯形ABCD中，AB∥CD，E、F、G、H分别 D G C
是梯形ABCD各边AB、BC、CD、DA的中点，当梯形ABCD H
F
满足条件 时，四边形EFGH是菱形，（请
填上你认为正确的一个条件即可） A E B
二、选择题（每小题4分，共8分）
（1）若
为锐角，且
是方程
的一个根，则
= --------（ ）
A 
B 
C 
D 和
（2）下列命题中真命题是 ----------------------------------------------（ ）
A
正三角形的内切圆半径与外接圆的半径之比为
B 正六边形的边长等于其外接圆的半径
C
圆外切正方形的边长等于其边心距的
倍
D 各边相等的圆外切多边形是正方形
三、解答题：（36分）
（1）解方程：
（6分）
（2）某日通过高速公路收费站的汽车，经统计共有3000辆，其中大汽车每辆次收费10元，小汽车每辆次收费5元；（每小题4分，共8分）
① 设这一天通过的小汽车辆次数为
总的通行收费
元，试写出与的函数关系式；
② 若估计汽车交通行费的3000辆中，大汽车不少于 20 %，且不大于 40 %，试求该收费站这一天收费总额的范围；
（3）如图，已知⊙O的圆心在⊙O
上，⊙O和⊙O相交于A、B两点，AC是⊙O的切线A为切点，交⊙O于点C，连结OC交⊙O于M，交AB于D，设⊙O的半径为R，⊙O的半径为
，且
，① 求
；（3分）
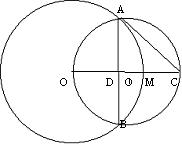
② 若OD = 9 cm，求AB的长；（4分）
③以M为圆心，MD为半径作⊙M，试问AC与⊙M的关系是什么？为什么？（3分）
（4）已知关于的二次函数
① 若关于的一元二次方程
的两根的平方和等于9，求
的值；（4分）
② 在 ① 的条件下，设这个二次函数的图象与轴从左到右交于 A、B两点，问在对称轴右边的图象上，是否存在点M，使锐角三角形AMB的面积为3？，若存在，请求出点M的坐标，若不存在 ，请说明理由。（4分）
② 在 ①、②的条件下，若点P是二次函数图象上的点，且∠PAM = 90，求
APM的面积。（4分）
参考答案：
I 卷
一、（1）；（2）
；（3）
（4）
；（5）
（6）1；（7）二；（8）
；（9）
；（10）；（11）四；（12）
；
（13）3 cm；（14）4，4；（15）DCFE；EGHF；
二、（16）B；（17）C；（18）B；
三、（19）
；（20）略；（21）第四小组的频数为14；第五小组的频率是0.16；跳绳次数的中位数落在第三小组；（22）证AEB∽ABC；
∽ 
；
；
II 卷
一、（1）
；（2）略；
二、（1）B；（2）B；
三、（1）
（2）①解：由题意知：交费车辆为3000辆次，若小汽车交费车辆次数为，则大汽车为
辆次；
所以 
③ 由题意知：
所以这一天收费站收费总额范围是不大于
元，不小于
元；
（3）①连结OA，AC为切线，OA
AC，在RtOAC中，OA = R，OC = 2 r ，
② ③①②③④