初中毕业数学暨升学考试试卷
(试卷总分150分，考试时间100分钟)
一、选择题（本题有12小题,每小题4分，共48分）下面每小题给出的四个选项中，只有一个是正确的,请把正确选项前面的字母填在题后的括号内
1．
的倒数是（ ）
A．2 B．－2 C． D．－
2．化简:
等于（ ）
A．2
B．
C．
D．
3．一元二次方程
的两根为
,
,则+的值是（ ）
A．3 B．－3 C．－1 D．1
4．2003年3月末,我国城乡居民储蓄存款余额达94600亿元，用科学记数法表示为（ ）
A．94.6×102 亿元 B．9.46×103亿元
C．9.46×104亿元 D．0.946×105亿元
5．若点(－1,2)是反比例函数
图象上一点,则k的值是（ ）
A．－ B． C．－2 D．2
6．如果梯形一底边长为6,中位线长为8,那么另一底边长为（ ）
A．4 B．7 C．10 D．14
7．圆锥的母线长为13cm,底面半径为5cm,则此圆锥的高线长为（ ）
A．6 cm B．8 cm C．10 cm D．12 cm
8．小明测得一周的体温并登记在下表(单位:℃)
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 | 周平均体温 |
| 体温 | 36.6 | 36.7 | 37.0 | 37.3 |
| 36.9 | 37.1 | 36.9 |
其中星期四的体温被墨迹污染.根据表中数据,可得此日的体温是（ ）
A．36.7℃ B．36.8℃ C．36.9℃ D．37.0℃
9．已知
,则代数式
的值为（ ）
A．－
B．
C．3 D．4
10．已知点G是△ABC的重心,GP∥BC交AB边于点P，BC=
，则GP等于（ ）
A．
B．
C．
D．
| 同 学 | 甲 | 乙 | 丙 |
| 放出风筝线长 | 100m | 100m | 90m |
| 线与地面交角 | 40° | 45° | 60° |
11．身高相等的三名同学甲、乙、丙参加风筝比赛，三人放出风筝线长、线与地面交角如右表（假设风筝线是拉直的），则三人所放的风筝中（ ）
A．甲的最高 B．丙的最高 C．乙的最低 D．丙的最低
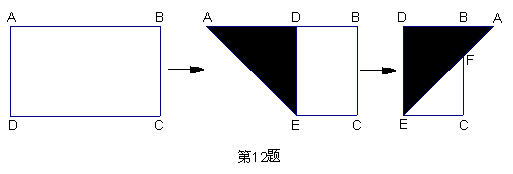
12．如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（ ）
A．4 B．6 C．8 D．10
二、填空题（本题有6小题，每小题5分，共30分）
13.如果节约16度水记作+16度，那么浪费6度水记作 度.
14.若正六边形的边长为2㎝，则此正六边形的外接圆半径为 ㎝.
15写出和为6的两个无理数 （只需写出一对）.
16.若半径不相等的两个圆有唯一公共点，则此两圆的公切线有 条.
17.若某人沿坡度ⅰ=3∶4的坡度前进10m，则他所在的位置比原来的位置升高 m.
18.抛物线
与x轴的正半轴交于A，B两点，与y轴交于C点，且线段AB的长为1，△ABC的面积为1，则b的值是
.
三、解答题（本题有7小题，共72分）下列各小题都必须写出解答过程
19.（本题8分）
计算：
.
20. （本题8分）
已知关于x的方程
有两个不相等的实数根，求k的取值范围.
21. （本题10分）
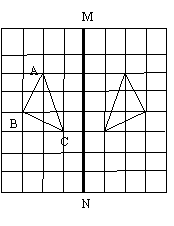
如图，在正方形网格上有一个△ABC.
（1）作△ABC关于直线MN的对称图形（不写作法）；
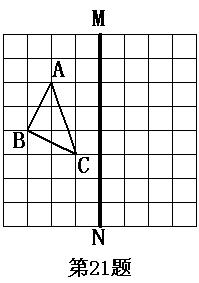（2）若网格上的最小正方形的边长为1，求△ABC的面积.
22. （本题10分）
已知二次函数的图象的顶点坐标为（－2，－3），且图象过点（－3，－2）.
（1）求此二次函数的解析式；
（2）设此二次函数的图象与x轴交于A，B两点，O为坐标原点，求线段OA，OB的长度之和.
23. （本题10分）
改革开放以来，我国国民经济保持良好发展势头，国内生产总值持续较快增长，下图是1998年－2002年国内生产总值统计图：
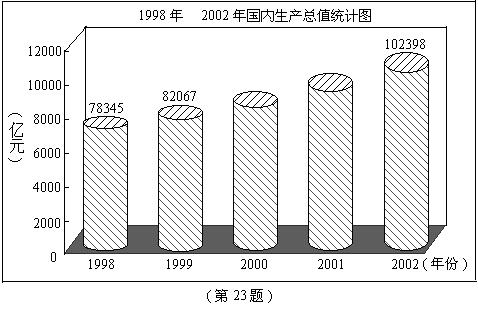
根据图中信息，解答下列问题：
（1）1999年国内生产总值是 ；
（2） 已知2002年国内生产总值比2000年增加12956亿元，2001年比2000年增加6491亿元，求2002年国内生产总值比2001年增长的百分率（结果保留两个有效数字）.
24. （本题12分）
如图，BC是半圆的直径，O是圆心，P是BC延长线上一点，PA切半圆于点A，AD⊥BC于点D.
（1） 若∠B=30°，问：AB与AP是否相等？请说明理由；
（2） 求证：PD·PO=PC·PB；
（3）
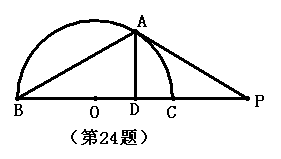若BD∶DC=
4∶1，且BC=10，求PC的长.
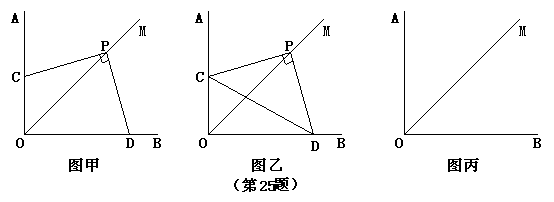
25. （本题14分）
已知∠AOB=90°，OM是∠AOB的平分线，按以下要求解答问题：
（1）将三角板的直角顶点P在射线OM上移动，两直角边分别与边OA，OB交于点C，D..
①在图甲中，证明：PC=PD；
②在图乙中，点G是CD与OP的交点，且PG=PD，求△POD与△PDG的面积之比.
（2）将三角板的直角顶点P在射线OM上移动，一直角边与边OB交于点D，OD=1，另一直角边与直线OA，直线OB分别交于点C，E，使以P，D，E为顶点的三角形与△OCD相似，在图丙中作出图形，试求OP的长.
绍兴市2003年初中毕业暨升学考试
数学试题参考案及评分标准
－、选择题（本题有12小题，毎小题4分，共48分）
1.A 2.B 3.A 4.C 5.C 6.C 7.D 8.A 9.B 10.B 11.B 12.C
二、填空题（本题有6小题，每小题5分，共30分）
13.－6 14.2 12.略 16.1或3（只填写其中的一个，给3分） 17.6 18.－3（填写±3，给3分）
三、解答题（本题有7小题，共72分）
19.（本题8分）
解：原式＝2－1+3---------------------------------------------------------------------------------------6分
＝4.----------------------------------------------------------------------------------------------2分
注：直接得出正确答案，给6分.
20.（本题8分）
解：△＝4－4（k－1）＝8－4k，--------------------------------------------------------------------2分
令△＞0，得8－4k＞0，-------------------------------------------------------------------------2分
解得 k＜2，
∴所求k的取值范围是k＜2.--------------------------------------------------------------------4分
21.（本题10分）
解：（1）作图正确给5分.
（2）此三角形面积为：
＝2×3－2
＝6－2－
.-------------------5分
注：直接得出正确答案，给4分。
22.（本题10分）
解：（1）∵函数图象的顶点坐标为（－2，－3），
∴设此二次函数的解析式为
.-------------------------------------2分
又∵图象过点（－3，－2），
∴－2＝
，
∴
.--------------------------------------------------------------------------2分
∴此二次函数的解析式是
.------------------------------1分
（2）设点A，B的横坐标分别为
，则是方程
的两根，
∴
，
，----------------------------------------------------2分
∴
，
.
∴OA＋OB＝
.--------------------------------3分
23.（本题10分）
解：（1）82067亿元.------------------------------------------------------------------------------------4分
注：只填写82067，给3分.
（2）设2000年国内生产总值为x亿元，则2001年、2002年分别为（x＋6491）亿元、（x＋12956）亿元。
由题意得：x＋12956＝102398，
解得 x＝89442，
则 x＋6491＝95933，-------------------------------------------------------------------------3分
.
答：2002年国内生产总值比2001年增长6.7%.-----------------------------------------3分
24.（本题12分）
解：（1）相等.------------------------------------1分
连结AO，
∵PA是半圆的切线，
∴∠OAP＝90°.
∵OA＝OB，
∴∠B＝∠OAB，
∴∠AOB＝2∠B＝60°，
∴∠APO＝30°，
∴∠B＝∠APO，
∴AB＝AP.--------------------------------------------------------------------------------------3分
（2）在Rt△OAP中，
∵AD⊥OP，
∴PA2＝PD·PO.------------------------------------------------------------------------------2分
∵PA是半圆的切线，
∴PA2＝PC·PB，
∴ PD·PO＝PC·PB.------------------------------------------------------------------------2分
（3）∵BD∶DC＝4∶1，且BC＝10，
∴BD＝8，CD＝2，
∴OD＝3.----------------------------------------------------------------------------------------2分
∵OA2＝OD·OP，
∴25＝3×OP，
∴OP＝
，
∴PC＝
.------------------------------------------------------------------------2分
25.（本题14分）
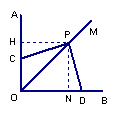
解：（1）①过P作PH⊥OA，PN⊥OB，垂足分别为H，N，
得∠HPN＝90°，∴∠HPC＋∠CPN＝90°.
而∠CPN＋∠NPD＝90°，
∴∠HPC＝∠NPD.-------------------------------------2分
∵OM是∠AOB的平分线，
∴PH＝PN.
又∵∠PHC＝∠PND＝90°，
∴△PCH≌△PDN，
∴PC＝PD.-------------------------------2分
②∵PC＝PD，∴∠PDG＝45°，
而∠POD＝45°，∴∠PDG＝∠POD.
又GPD＝∠DPO，
∴△POD∽△PDG.-------------------3分
.------------2分
（2）若PC与边OA相交，
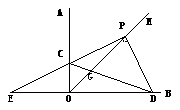∵∠PDE＞∠CDO，∴△PDE∽△OCD，∴∠CDO＝∠PED，
∴CE＝CD，而CO⊥ED，
∴OE＝OD，
∴OP＝
ED＝OD＝1.-----------------2分
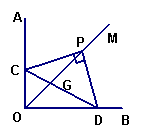
若PC与边OA的反向延长线相交，
过P作PH⊥OA，PN⊥OB，垂足分别为H，N，
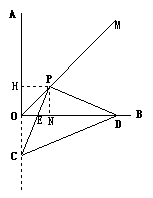∵∠PED＞∠EDC，∴PDE∽△ODC，∴∠PDE＝∠ODC.
∵∠OEC＝∠PED，∴∠PDE＝∠HCP.
而PH＝PN， Rt△PHC≌Rt△PND，
∴HC＝ND，PC＝PD，∴∠PDC＝45°，
∴∠PDO＝∠PCH＝22.5°，
∴∠OPC＝180°－∠POC－∠OCP＝22.5°，
∴OP＝OC. 设OP＝x，
则OH＝ON＝
，
∴HC＝DN＝OD－ON＝1－，而HC＝HO＋OC＝＋x，
∴1－＝＋x，∴x＝
，
即OP＝.------------------------------------------------------------------------------3分