初中部初三数学第二次月考试卷
一、 选择题（本题共12小题，每题4分，共48分）
1、如果实数
，那么a与b（ ）
A、相等 B、互为相反数 C、互为倒数 D、上述三种情况都可能
2．用代数式表示“2a与3的差”为（ ）
A．2a－3 B．3－2a C．2(a－3) D．2(3－a)
3、下列方程中，两根之和是
的是（
）
A、
B、
C、
D、
4、函数
中自变量x的取值范围是（
）
A、
B、
C、
D、
5、二次函数
的顶点坐标是（
）
A、（1，3） B、（－1，3） C、（1，－3） D、（－1，－3）
6、如图，某同学把一块三角形的玻璃打碎成三块，
现要到玻璃店里去配一块形状与大小都完全相同的
玻璃，则最省事的方法是（
）
② ③
A、带①去 B、带②去 ①
C、带③去 D、带①②去
7、用换元法解方程
时，若设
，则原方程可化为（ ）
A、
B、
C、
D、
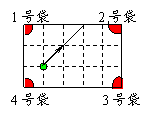8、6、图2是一个经过改造的台球桌面示意图，图中四个角上的阴影部分分别表示四个入球孔。如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入的球袋是（
）
A．一号袋 B．二号袋 C．三号袋 D．四号袋
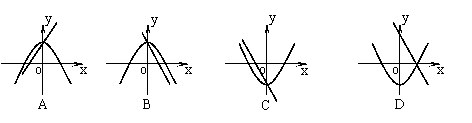9、在同一直角坐标系中，一次函数y＝ax＋c和二次函数y＝ax2＋c的图像大致为（ ）
10、方程
的实数根有（ ）
A、3个 B、2个 C、1个 D、0个
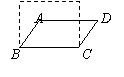11、如右图，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于 。
A、15° B、30° C、45° D、60°
12、若二次函数
与x轴有两个不同交点，则k的取值范围是（ ）
A、k≥0 B、k≥－4 C、k＞－4 D、k＞0
二、填空题（本题共6小题，每题5分，共30分）
13．写出一个与
不相等的无理数，使它与相乘的积为有理数。这个数是：
。
14．如右图，数轴上的点A所表示的是实数a ，
则点A到原点的距离是 。
15．小新家今年6月份头6天用米量如下表：
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 |
| 用米量（千克） | 0.9 | 0.8 | 0.6 | 0.9 | 0.8 | 1.0 |
请你运用统计知识，估计小新家6月份（按30天算）用米量为 千克。
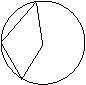
16、如右图，已知⊙O中，A、B、C都在圆上，且∠BAC=124°，则∠COB= 度 。
17、方程组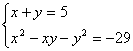
的解是
。
18、观察下列计算：
，
，
……，从计算结果中找出规律，并利用这一规律计算：
。
三、解答题：（共7题，要写出必要的解题过程，共8+8+9+9+12+12+14=72分）
19、
如图所示：已知□ABCD中，E、F是对角线BD上的两点， A D
且BE=DF，求证：（1）△ADE≌△CBF； E
（2）AE∥CF F
B C
20、已知
，
，求代数式
的值。
21．已知关于x的方程
。
（1）当m取什么值时，原方程没有实数根；
（2）对m选取一个合适的非零整数代入方程，并求这个方程两个实数根的平方和.
22、某商场今年5月份销售一种新产品，其进价是每件80元，售价是每件120元，当月销售量国600件。六月份，经市场调查得知：该新产品售价每降低1元时，每月的销售量将增加60件，但每件的最低售价不能低于106元。为增加利润，减少库存，商场决定适当降低该新产品的售价。（1）写出6月份降低该产品的售价后，商场所获利润y元与每件降低x元（x取整数）之间的函数关系式，并指出自变量的取值范围；
（2）每件产品降价多少元时，商场6月份销售该产品所获利润比5月份销售该商品利润增加50%？[注：利润=销售量×（产品售价－产品进价）]
23．仔细观察下图，认真阅读对话：
根据对话的内容，试求出饼干和牛奶的标价各是多少元？
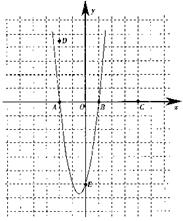
24．在平面直角坐标系中，给定以下五点A（－2，0），B（1，0）C（4，0），D（－2，
），E（0，－6），从这五点中选取三点，使经过这三点的抛物线满足以平行于y轴的直线为对称轴.我们约定：把经过三点A、E、B的抛物线表示为抛物线AEB（如图所示）.
（1）问符合条件的抛物线还有哪几条？不求解析式，请用约定的方法一一表示出来；
|
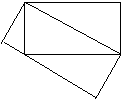
25、如图1，△ABC是直角三角形，∠C=90°，现将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB（如图2），
A
A
D
A
E B
C B C C B
图1 图2 F 图3
解答下列问题：
（1）设图2中的矩形ACBD和矩形AEFB的面积分别为
和
，则
；（填上“＜”、“＞”或“＝”）。
（2）如图3中，△ABC是钝角三角形，按上文中的要求把它补成矩形，那么可以画出 个矩形，画在图3中；
（3）如图4中，△ABC是锐角三角形，且三边满足BC＞AC＞AB，按上文中的要求把它补成矩形，那么可以画出 个矩形，画在图4中；
A
B C
图4
（4）在第（3）小题所画的几个矩形中，哪个矩形的周长最小，写出你的证明过程。