初中第五册数学测试题

初中第五册数学测试题

　　　　姓名____________________　　　得分____________________

一、选择题(本大题共14小题，每小题3分，共42分)

1、下列方程中，有实数根的是（　　　 ）

A  (-x)²+4=0　　B  2x²―x+1=0　 C  x²+x+1=0 　D  2x²―x―=0

2、已知cosα=，那么锐角α的度数是（　　　 ）

A　60°　　　　B  45°　 　　　 C　30°　 　　 D  75°

3、函数y=3x+2中自变量x的取值范围是（　　　 ）

A　x≠―　　 B　x≥― 　　　C  x＜―　　D  全体实数

4、若点P（-3，a）与点Q（b,3）关于原点对称，则b^a为（　　　 ）

A  27　 　　　 B  –27 　　　　 C 　　　　 D　―

5、函数y=-x―1的图象不经过（　　　 ）

A 第一象限　　 B 第二象限　　　C 第三象限　  D 第四象限

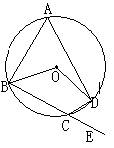
6、如图，四边形ABCD内接于⊙O，E是BC延长线上一点，∠DCE=55°，那么∠BOD等于（　　　 ）

A 110°　　　 B 135　　　　 C　55°　　 D 125°

7、若点（-1，y₁），（2，y₂），（3，y₃）都在反比例函数y=的图象上，则（　　　 ）

A y₁＜y₂＜y₃B y ₂＜y₁＜y₃　C y₃＜y₂＜y₁　D y₁＜y₃＜y₂

8、求一元二次方程，使它的两个根是－3，2，所求方程是（　　　）

A x²―x+6=0 　B x²―x―6=0  C x² +x+6=0　D x² +x―6=0

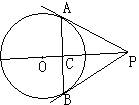9、如图，P是⊙O外一点，PA，PB是⊙O的切线，切点分别是A、B，AB与OP交于点C，若PB=6，AB=8，则tan∠APB的值为（　　　 ）

A 　　　　　B 　　　　　C 　　 D

10、二次函数y=mx²－6x＋3m＋m²的图象经过原点，当y＞0时，自变量x的取值范围是（）

A  x ＜-2 　　B  x＞0　　　 C  x ＜-2或 x＞0 　 D  -2＜x＜0

11、Rt△ABC中，∠C=90°，若cosA=，那么cotB=（　　　）

A 　　　　　B 　　　　C 　　　　　D

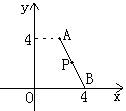
12、如图，已知A、B坐标分别为A（2，4），B（4，0），P为AB的中点，若将线段AB向右平移3个单位后，移动后P点坐标为（　　　）

A (3，2)　　　 B(6，2)　　　C(6，4)　　　 D(3，3)

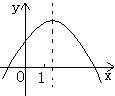
13、已知二次函数y=ax²+bx+c(a≠0)的图象如图，下列不等式中，不正确的式子的是（　　　 ）

A a＜0　　　 B b ＞0　　　C c＞0 　　　D 2a+b＜0

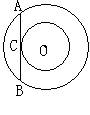14、如图，在同心圆中，大圆的弦AB切小圆于C，若弦AB=4，则该圆环面积为（　　　 ）

A　4π　B 5π　C 6π　D 7π

二、填空题（本大题共8小题，每小题4分，共32分）

15、以原点为圆心，以为半径的圆与y轴的交点坐标为_____　　____。

16、计算：tan60°――2^-1=_________________。

17、已知a、b是方程2x²―6x―1=0的两根，则代数式(ab)^a+b=_________。

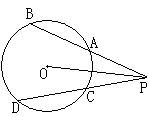­­­­­­­­­­­­­­­­­­­­18、如图，弦BA、DC的延长线交于⊙O外一点P，如果要使∠BPO=∠DPO，那么需添加一个条件是__________________________（只填一个即可）。

19、已知函数y=-2x²+x，当x=______时，函数有最大值为_______________。

20、直线y=kx+k²经过点（1，2），且不经过第三象限，那么与它在同一直角坐标系内的双曲线y=经过_________________象限。

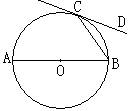
21、如图，AB是⊙O的直径，CD切⊙O于C，若∠BCD=

25°，则∠B=_____________。

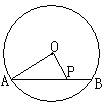
22、如图，在⊙O中，P 是AB上点，PA=6，PB=4，PO=5，则cosA=__________。

三、解答下列各题（本大题共4小题，每题6分，共24分）

23 、解方程：x―=2

24、解方程组：

25、计算：cos30°―+tan²60°+(cos75°―tan25°)

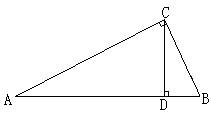26、如图，在△ABC中，已知∠ACB=90°，CD⊥AB于D，AC=6，BD=3。

求：（1）cosA　　（2）S△ABC

四、解答下列各题（本题共4小题，共27分）

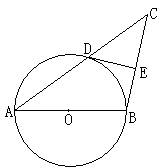
27、已知：如图，AB是⊙O的直径，⊙O过AC的中点D，DE切⊙O于点D，BC和DE交于点E。（6分）

求证：DE⊥BC

28、汽车由A地驶往相距630千米的B地，它的速度是70千米/时，（1）写出汽车距B地的路程s（千米）与行驶时间t（时）的函数关系式，并求出自变量t的取值范围；（2）当汽车还差210千米到达B地时，它行驶了多少时间？（6分）

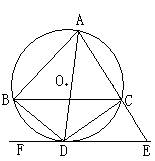29、如图，已知△ABC内接于⊙，AD平分∠BAC，交⊙O于点D，过D作⊙O的切线与AC的延长线交于点E。（8分）

（1）求证：BC∥DE

（2）若AB=3，BD=2，求CE的长。

30、盐都商场今年1月份销售额为60万元，2月份销售额下降10%，后改进经营管理，月销售额大幅度上升，到4月份销售额已达96万元，求3、4月份销售额平均每月的增长率是多少？

五、（本题共2小题，共16分）

31、菱形ABCD的周长为20，两对角线交于点O，且OA、OB为一元二次方程x²―(2m―1)x+4(m―1)=0的两个根，试求m的值。

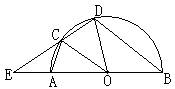32、如图，AB是半圆O的直径，AB=4，C、D是半圆上的两点，且AC=CD，DC的延长线与BA的延长线相交于E。（1）求证：OC∥BD（2）设∠AOC=α，若sin=，cosα=，求EC的值。

六、如图，直线y=－x+分别与x轴、y轴交于点A、B，⊙E经过原点O及A、B两点。

（1）C是⊙E上一点，连结BC交OA于点D。若∠COD=∠CBO。求点A、B、C的坐标。

（2）写出图象经过O、C、A三点的二次函数的解析式。

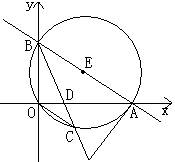（3）若延长BC到P，使DP=2，连结PA，试判断直线PA与⊙E的位置关系，并说明理由。（9分）