初中第五学期末教学质量测试1
数 学 试 卷
班级______ 姓名___________
第 Ⅰ 卷（选择题，共42分）
一、选择题：本大题共14个小题，每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的，把它选出来涂在答题卡上．
1．已知x=－1是方程x2＋mx＋1＝0的一个根，那么m的值是( )
A．0 B．1 C．2 D．－2
2．若关于x的一元二次方程x2－2(k－2)x＋k2=0有两个不相等的实数
根，则实数k的取值范围是( )
A．k＞1 B．k<1 C．k＞－1 D．k<－1
3、点P(－3，－4)关于X轴对称的点的坐标是( )
A．(－3，4) B．(3，4) C．(3，－4) D．(－4，－3)
4．直线y=kx过点（
，－
），那么它还通过点( )
A、(－，) B、(－，) C、(，) D、(－，－)
5．直线y=kx＋b（k≠±1），若b减少一个单位，则它的位置将( )
A．向左平移一个单位 B．向右平移一个单位
C．向下平移一个单位 D．向上平移一个单位
6．化简
的结果为( )
A、－
B、0 C、
D、2
7．设α、β是关于x的方程x2－2（2m＋1）x＋3m2－4=0的两个根，
且
=2，则m的值为( )
A、1或
B、1或－ C、－1或 D、－1或
8．从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品，对其
中使用寿命跟踪调查，结果如下（单位：年）
甲：3，4，5，6，8，8，8，10
乙：4，6，6，6，8，9，12，13
丙：3，3，4，7，9，10，11，12
三个厂家在广告中都称该产品的使用寿命是8年，由此可知甲、乙、丙三个厂家在广告中分别运用了这组调查数据的特征数是( )
A．平均数、众数、中位数
B．众数、平均数、中位数
C．众数、中位数、平均数
D．平均数、中位数、众数
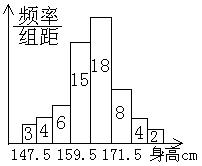
9．如图所示是某地初中三年级男学生的身
高情况频率分布直方图，则各组中频率最
大为( )
A．0.05 B、0.1 C．0.3 D．1
10．在直角三角形ABC（C为直角）中，a、b、c分别是角A、B、C
的对边，下面的等式中，错误的是( )
A．a＝c·sinA B．b＝c·cosA
C．a＝b·tanA D．b＝a·sinA
11．当锐角α<450时，角α的正弦值和余弦值的大小关系应是( )
A．sinα<cosα B．sinα＞cosα
C．slnα＝cosα D．不能确定
12．已知AB是⊙O的直径，弦BC＝4，则弦AC的弦心距是（ ）
A．1 B．2 C．3 D．4
13．在⊙O中，若AB弧=2CD弧，则弦AB与CD的关系是( )
A．A B＝2CD B．AB＜2CD C．AB＞2CD D．CD<AB<2CD
14．若AB是⊙O的直径，半径OC⊥AB，F是OC的中点，过F作
DE∥AB交圆于D、E，则∠CBD＝( )
A．600 B．450 C．300 D．150
第 Ⅱ 卷（非选择题，共58分）
二、填空题：本大题共4小题，每小题4分，共16分．
15．将x2＋4x－1分解因式为__________。
16．已知一个水池的容量为100 m3，每小时的注水量为xm3，注满水
池所需时间为y小时，则y关于x的函数解析式为__________
17．已知tan2α－4 tanα＋＝0，则锐角α为__________
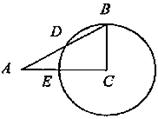18．如图，RtΔABC中，∠A=280，以C为圆心，
BC为半径的圆C交AB、AC边于D、E，则
DE弧度数为__________．
三、解答题：本大题共6小题，共42分．解答应写出文字说明、证明过程或演算步骤．
19．（本题满分7分）解方程：x＋
＝1＋2
．
20．己知双曲线y=
（k≠0）上有一点P，它的横坐标与纵坐标恰
好是方程t2－4t－2＝0的两个根．
（1）求双曲线的解析式；（2）求点P与原点O的距离．
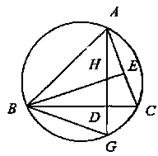21．如图，ΔABC的高AD、BE相交于H，AD的延长线交外接圆于点G．
求证：D为HG的中点．
22．已知：四边形有2条对角线，五边形有5条对角线，六边形有9条对角线，那么是否存在对角线有152条的多边形呢？说明理由．
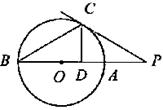23．如图，PC为⊙O的切线，C为切点，PAB是经过点O的割线，CD⊥AB于D，若tanB=，PC＝10cm，求ΔBCD的面积．
24．渔场中鱼群的最大养殖量为m吨，为保证鱼群的生长空间，实际养殖量不能达到最大养殖量，必须留出适当的空闲量．已知鱼群的年增长量y吨和实际养殖量x吨与空闲率的乘积成正比，比例系数为
．（空闲量=最大养殖量－实际养殖量，空闲率=
）
（1）写出y关于x的函数关系式，并指出自变量x的取值范围;
（2）求鱼群年增长量的最大值．