初中三年级数学（上）期末监测
（全卷共五个大题，满分100分，考试时间90分钟）
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 | 总分人 |
| 分数 |
| 得分 | 评分人 |
一、填空题（本大题共10个小题，每小题2分，共20分）
1、若
、
是方程
的两个根，
那么+=
，
=
2、在平面直角坐标系中，已知点
和
，则PQ=
3、若方程
的判别式的值是4，则P=
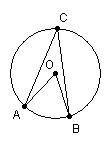
4、如图，在⊙
中，若圆心角∠AOB=80°，
则圆周角∠ACB=
5、在Rt⊿ABC中，∠C=90°，AB=13，AC=12，
则cosB= , tanB=
6、已知两条平行弦AB、CD的长为6㎝和8㎝，圆的半径为5 ㎝，
则两平行弦之间的距离为 ；
7、过原点且与
平行的直线是
；
8、如图，⊙
的半径为13，弦
=24，
是弦上的一个动点，那么
的长的取值范围是____________________
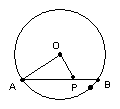
9、已知PA 切⊙于A，弦AB⊥OP于D，AB=8，OD=3，
则PA=
10、点P
在第三象限，则直线
经过第
象限
| 得分 | 评分人 |
二、选择题（本大题共10个小题，每小题3分，共30分，将唯一正确的答案代号填在题后的括号里）
1、在Rt△ABC中，∠C=90°，若∠B=2∠A，则sinA=（ ）
（A）
（B）
（C）
（D）
2、点P
关于原点的对称点的坐标是（
）
（A）
（B）
（C）
（D）
3、关于
的方程
的根的情况是（ ）
（A） 有两个不相等的实数根 （B）总有实数根
（C） 有两个相等的实数根 （D）没实数根
4、函数
中自变量的取值范围是（
）
（A）
（B）
（C）
（D）
5、一次函数
的图象不经过的象限为（
）
（A） 第一象限 （B）第二象限
（C）第三象限 （D）第四象限
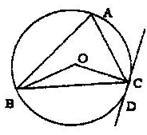
6、若如图，△ABC内接于⊙O，
，DC是过C点的切线，则
等于（ ）
（A）
（B）
（C）
（D）
7、下列图形中对称轴最多的是（ ）
（A）等边三角形 （B）矩形 （C）正方形 （D）圆
8、方程组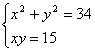
的解是（
）
（A）
（B）
（C） （D） 
9、将二次三项式
进行配方，正确的结果应为（ ）
（A）
（B）
（C）
（D）
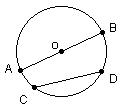10、如图，AB是⊙O的直径，CD是弦。
若AB=10㎝，CD=8㎝，那么A，B两点到直线CD的距离之和为（ ）
（A）12㎝ （B）10㎝ （C）8㎝ （D）6 ㎝
| 得分 | 评分人 |
三、（本大题共4个小题，每小题6分，共24分）
1、解方程
2、计算
3、已知一次函数的图象经过点
和点
，求这条直线的解析式，并画出这条直线。
4、已知关于的方程
（1）求证：方程有两个不相等的实数根；
（2）设方程的两根为
，如果
，求
的取值范围.
| 得分 | 评分人 |
四、（本大题共2个小题，每小题6分，共12分）
1、如图，AB是⊙的直径，AD⊥CD，BC⊥CD，且AD+BC=AB
（1） 
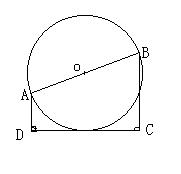求证：⊙与CD相切；
（2） 若CD=3，求AD·BC的值.
2、甲、乙两个商店到同一厂家按同样价格购进同一种方便面，共进货100箱，但甲、乙两店进货数量不同。由于两店所处的位置不同，因此，两店的销售价格也不同，两店将所进的方便面全部销售完后，销售额相同，如果将甲、乙两店的进货量互换销售，并保持两店的原销售价格不变，由此甲店销售额为2700元，乙店销售额为1200元，问甲、乙两店谁在原销售中获利较多，为什么？
| 得分 | 评分人 |
五、（本大题共2个小题，每小题7分，共14分）
1、通过阅读所得的启示来证明问题（阅读中的结论可以直接用）
阅读：如图，△ABC内接于⊙，∠EAC=∠B。
求证：AE与⊙相切于点A。
证明：作直径AF，连结FC，则∠AFC+∠CAF=90°
∵∠B=∠AFC ∴∠B+∠CAF=90°。
又∵∠CAE=∠B，∴ ∠CAE+∠CAF=90°。
∴AE与⊙相切于点A。
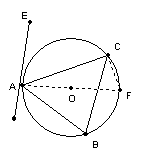
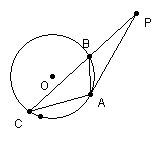问题：如图，已知△ABC内接于⊙，P是CB延长线上一点，
连结AP，且
，
求证：PA是⊙的切线
2、食品厂生产的一种巧克力糖每千克成本为24元，其销售方案有如下两种：
|
项目 | 一月 | 二月 | 三月 |
| 销售量 （千克） | 550 | 600 | 1400 |
| 利润 （元） | 2000 | 2400 | 5600 |
月份方案1若直接给本长设在万州的门市部销售，则每千克售价为32元，但门市部每月需要上缴有关费用2400元。
方案2若直接批发给超市销售，则出厂价为每 千克28元。
若每月只能按一种方案销售，且每种方案都能按月销售完当月产品，设该厂每月的销售量为千克。
（1）如果你是厂长，应该如何选择销售方案，可使工厂当月所获利润更大？
（2）厂长看到会计送来的第一季度销售量与利润关系的报表（如上表）后，发现该表填写的销售量与实际有不符之处，请找出不符之处，并计算第一季度的实际销售总量。