九年级数学第二学期期中试卷
得分
一、填空题（第1—6题每格1分，第7—10题每格2分，共18分）
1． 64的算术平方根是 ． 0.000018用科学记数法表示为___ __.
－2a2·a3=
。 若
，则m:n= ．
2.分解因式：xy-x2= ．
3.用计算器求值： ⑴cos14º28´= ； （取四个有效数字）
⑵若tan A=0.0789,则∠A= .（精确到分）
4. 如果反比例函数y=
的图像经过真A(3，-4)，那么k的值是
5.已知⊙O的半径
,O到直线
的距离OA=3,点B,C,D在直线上,且AB=2,AC=4,AD=5,则点B在⊙O
点C在⊙O
6．亮亮想制作一圆锥模型，这个模型的侧面是用一个半径为9cm，圆心角为240°的扇形铁皮制作的，再用一块圆形铁皮做底。请帮他计算这块铁皮的半径为 cm
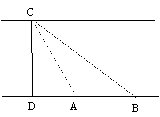
7．如图，在△ABC中，∠ACB=900，BC=4，AC=5，CD⊥AB，则
tan∠BCD=____________
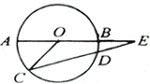
8．如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，已知AB=2DE，∠E=18°，则∠AOC的度数为 ．
9．某市民政部门今年元宵节期间举行了“即开式社会福利彩票”销售活动，设置彩票3000万张（每张彩票2元），在这些彩票中，设置了如下的奖次：
| 奖金(万元) | 50 | 15 | 8 | 4 | … |
| 数量(个) | 20 | 20 | 20 | 180 | … |
如果花2元钱购买1张彩票，那么能得到8万元以上(包括8万元)大奖的概率是 。
10．请写出一个开口向上，对称轴为直线x=2，且与y轴的交点坐标为(0，3)的抛物线的解析式 。
二、选择题（每小题2分，共18分）
11．当a＜0时，化简
得
（ ）
（A）－2 （B）0 （C）1 （D）2
12二次函数y=－x2－2x+2的顶点坐标对称轴分别是
（ ）
（A）(1, 3), x=1
（B）(－1, 3), x=1
（C）(－1, 3), x=－1 （D）(1, 3), x=－1
3．下列图形中，既是轴对称，也是中心对称的图形是 ( )
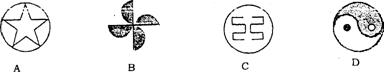
14．小明把自己一周的支出情况，用图3所示的统计图来表示，下面说法正
确的是
（ ）
(A)．从图中可以直接看出具体消费数额
(B)．从图中可以直接看出总消费数额
(C)．从图中可以直接看出各项消费数额占总消费额的百分比
(D)．从图中可以直接看出各项消费数额在一周中的具体变化情况
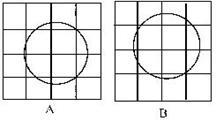
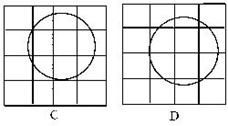
15下图中每张方格纸上都画有一个圆，
只用不带刻度的直尺就能确定圆心位置的是 ( )
|
16．右边给出的是2004年3月份的日历表，任意圈出一竖列上相邻的三个数，请你运用方程思想来研究，发现这三个数的和不可能是 （ ）
(A)．69 (B)．54
(C)．27 (D)．40
17．下列说法不正确的是
（ ）
（A）以等腰三角形顶角的顶点为圆心，底边上的高
为半径的圆与底边相切
（B）若两个三角形的边长为8、6、4和4
、3、2，则这两个三角形相似
（C）垂直于弦的直径平分这条弦，并且平分弦所对的两条弧
（D）命题“两圆外离，则两圆无公共点”的逆命题是真命题
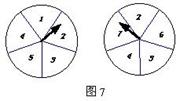
18．图7所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时落在偶数上的概率是 （ ）
A．
B．
C．
D．
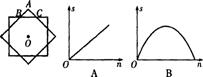
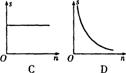
19．如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心O作0°～90°的旋转，那么旋转时露出的△ABC的面积(S)随着旋转角度(n)的变化而变化，下面表示S与n的关系的图象大致是 ( )
三、（每题5分，共15分）
20、计算： 
（不用计算器）
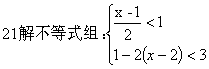22 化简 
四、解答题(23-26题每题8分，27-29题每题9分，30题10分)
23．（本题8分）下表是明明同学填写实习报告的部分内容：
| 题目 | 在两岸近似平行的河段上测量河宽 |
| 测量目标图示 |
|
| 测得数据 | ∠CAD=60° AB=20米 ∠CBD=45° ∠BDC=90° |
请你根据以上的条件，计算出河宽CD（结果保留根号）。
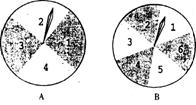
24．(本题8分)如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字．有人为甲、乙两人设计了一个游戏，其规则如下：(1)同时自由转动转盘A与B (2)转盘停止后，指针各指向一个数字(如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止)，用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜(如转盘A指针指向3，转盘B指针指向5，3×5=15，按规则乙胜)．你认为这样的规则是否公平?请说明理由；如果不公平，请你设计 一个公平的规则，并说明理由．
25．（本题8分）如图，AB是⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D。问：AC平分∠DAB吗？请说明理由？
26、（本题8分）某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变。有关数据如下表所示：
| 景点 | A | B | C | D | E |
| 原价（元） | 10 | 10 | 15 | 20 | 25 |
| 现价（元） | 5 | 5 | 15 | 25 | 30 |
| 平均日人数（千人） | 1 | 1 | 2 | 3 | 2 |
（1） 该风景区称调整前后这5个景点门票的平均收费不变，平均日总收入持平。问风景区是怎样计算的？
（2） 另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，实际上增加了约9.4%。问游客是怎样计算的？
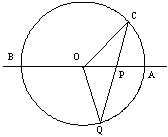
27（9分）．如图，直线AB经过圆O的圆心，且于圆O相交于A、B两点，点C在圆O上且∠AOC=300，点P为直线AB上一动点（与点O不重合），直线PC与圆O相交于点Q，是否存在点P，使得QP=QO，如果存在，那么这样的点P共有几个？并相应求出∠OCP的大小；如果不存在，请说明理由。
28． (9分)如图A0A1是半圆o的半径，A0A1=2，A2、A3、……Ak、Ak+1、……是半圆上的点，∠A0A1A2=10，∠A1A2 A3=20，∠A2 A3 A4=30,……，∠Ak-1 AkAk+1=k0（k为正整数），
的长记为L0 ，
的长记为L1 ，……，AkAk+1的长记为Lk 。
（1）填空：L0= ，L1= ，L2= ，L3= 。
（2）用k的代数式表示：Lk= ;
（3）利用计算器探求当k至少为多少时，Lk开始小于1。
30.某企业投资100万元引进一条农产品加工生产线，若不计维修、保养费用，预计投产后每年可创利33万元。该生产线投产后，从第一年到第
年的维修、保养费用累计为
(万元), 且
，若第一年的维修、保养费为2万元，第2年的为4万元。
⑴ 求的解析式；
⑵投产后，这个企业在第几年就能收回投资？