九年级数学周考试卷

九年级数学周考试卷

第一部分　　选择题（共28分）

一、选择题（下列各题所给答案中,只有一个答案是正确的.1-8每小题2分,9-12每小题3分,共28分）

(　　)1．(03滨州)的倒数是

A．　　　　 B．　　　　　　C．　 　　　　D．

(　  )2.下列运算正确的是

　　　A.　　　　　　　 B.(03滨州)

　　　C.　　　　 D.

(　  )3.2003年10月15日9时10分,我国神舟五号载人飞船准确进入预定轨道.16日5时59分,返回舱与推进舱分离,返回地面.其间飞船绕地球共飞行了14圈,飞行的路程约60万千米,则神舟五号飞船绕地球平均每圈约飞行 (用科学记数法表示,结果保留三个有效数字)

　　　A. 4.28×10⁴千米 B. 4.29×10⁴千米　 C. 4.28×10⁵千米　 D. 4.29×10⁵千米　

(　　 )4.△ABC中,AB=3,BC=4,则AC边的长满足

　　　A．AC=5　　　　B．AC1　　　　 C．AC7　　　　 D. 1AC7

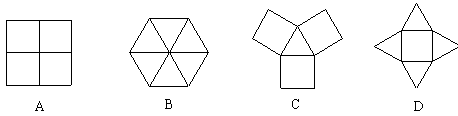(　　 )5.下列由正三角形和正方形拼成的图形中是轴对称图形而不是中心对称图形的是

(　　 )6.(03太原)圆内接四边形ABCD中,若∠A:∠B:∠C=1:2:5,则∠D等于

　　　　A. 60°　　　　B. 120°　　　　　 C. 140°　　　　　 D. 150°　

(　　 )7. (03大连)已知⊙O₁和⊙O₂的半径分别为2和5,O₁O₂=7,则⊙O₁和⊙O₂的位置关系是

　　　A. 外切　 　　　B. 内切　 　　　　C. 相交　　 　　　D. 相离

(　　)8.小芳和爸爸、妈妈三人玩跷跷板,三人的体重一共为150千克,爸爸坐在跷跷板的一端；体重只有妈妈一半的小芳和妈妈一同坐在跷跷板的另一端.这时,爸爸的那一端仍然着地.请你猜一猜小芳的体重应小于

　　A. 49千克　　　　 B. 50千克　　　　 C. 24千克　　　　 D. 25千克

(　　 )9.若代数式的值是常数2,则a的取值范围是

　　A.≥4　　　　　 B.≤2　　　　　 C. 2≤a≤4　　　　 D. 或

(　 )10.四边形ABCD中,AB∥CD,且AB、CD长是关于x的方程的两个实数根,则四边形ABCD是

　　　　A. 矩形　　　 B. 平行四边形　　 C. 梯形　　　　　 D. 平行四边形或梯形

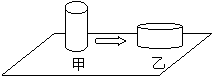
(　　 )11.用某种金属材料制成的高度为h的圆柱形物体甲如右图放在桌面上,它对桌面的压强为1000帕,将物体甲锻造成高度为h的圆柱形的物体乙(重量保持不变),则乙对桌面的压强为

　　A．500帕　　　　 B．1000帕　　　　C．2000帕　　　　D．250帕

(　　)12.(02重庆市)给出下列四个命题：

（1）如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形；

（2）若点A在直线y=2x-3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；

（3）半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个；

（4）若A（a,m）、B（a -1,n）(a0)在反比例函数的图象上,则mn.

其中,正确命题的个数是

　　A. 1个　　　　　　B. 2个　　　　　　C. 3个　　　　　　D. 4个

第二部分　　非选择题（共102分）

二、填空题（每题3分,共24分）

13.(02上海市)下列各数, ,,,中,无理数共有＿＿＿个.　

14.函数的自变量x的取值范围是＿＿＿＿＿.

15.如果二次根式x²－ax+15在整数范围内可以分解因式，那么整数a的取（只需填写一个你认为正确的答案即可）　　　 。

16.如图有一个边长为1.5㎝的正六边形，如果要剪一张圆形纸片完全盖住这个图形，那么这张圆形纸片的最小半径为　　　　 cm。

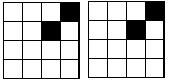17.由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）。请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它成为轴对称图形。

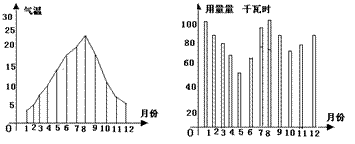18.图1表示某地区2003年12个月中每个月的平均气温，图2表示该地区某家庭这年12个月中每月的用电量。根据统计图，请你说出该家庭用电量与气温之间的关系（只要求写出一条信息即可）：　　　　　 _______________ 。

19.△ABO中，OA=OB=5，OA边上的高线长为4，将△ABO放在平面直角坐标系中，使点O与原点重合，点A在x轴的正半轴上，那么点B的坐标是　　　。

20.为了能有效地使用电力资源,我市供电部门最近进行居民峰谷用电试点,每天8:00至21:00用电每千瓦时0.55元（“峰电”价）,21:00至次日8:00每千瓦时0.30元(“谷电”价)．王老师家使用“峰谷”电后,五月份用电量为300千瓦时,付电费115元,则王老师家该月使用“峰电” ______千瓦时.

三、解答题（本大题2小题；计10分）

21.计算：　　　 22．化简：

23. （本题满分6分）

分别解不等式和，再根据它们的解集写出x与y的大小关系.

24.　（本题满分6分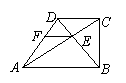）如图，直角梯形ABCD中，，，对角线，垂足为E，AD=BD，过点E作交AD于F.

求证：（1）AF=BE；（2）AF²=AE·EC.

25．（本题满分8分）已知关于x的一元二次方程.

（1）　　　 当m为何值时，这个方程有两个相等的实数根；

（2）　　　 如果这个方程的两个实数根x₁、x₂，满足，求m的值.

26. （本题满分7分）如图10，一次函数的图象与反比例函数的图象交于M、N两点.

（1）求反比例函数和一次函数的解析式；（8分）

（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.（4分）

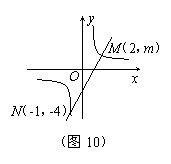
27. （本题满分8分）用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.

(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.

(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程的两个实数根,试求出原矩形纸片的面积.

28.(本题满分8分)　 西北某地区为改造沙漠，决定从2002年起进行“治沙种草”，把沙漠地变为草地，并出台了一项激励措施：在“治沙种草”过程中，每一年新增草地面积达到10亩的农户，当年都可得到生活补贴费1500元，且每超出一亩，政府还给予每亩a元的奖励.另外，经治沙种草后的土地从下一年起，平均每亩每年可有b元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况：

年　份	新增草地的亩数	年总收入
2002年	20亩	2600元
2003年	26亩	5060元

(注：年总收入＝生活补贴费＋政府奖励费＋种草收入)

　　⑴试根据以上提供的资料确定a，b的值；

⑵从2003年起，如果该农户每年新增草地的亩数均能比前一年按相同的增长率增长，那么2005年该农户通过“治沙种草”获得的年总收入将达到多少元？

29．（本题满分9分）如图①，E为线段AB上的一点，AB=4BE，以AE、BE为直径在AB的两侧作半圆，圆心分别为O₁、O₂，AC、BD分别是两半圆的切线，C、D为切点.

（1）　　　 求证：AC=BD；

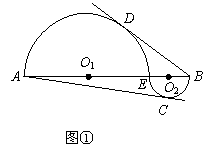
（2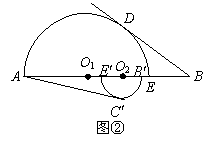）　　　 现将半圆O₂沿着线段BA向点A平行移动，如图②，此时半圆O₂的直径在线段AB上，是半圆O₂的切线，是切点，当何值时，以A、 、O₂为顶点的三角形与相似.

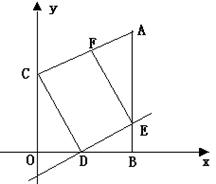30．（本题满分10分）如图在平面直角坐标系内，点A与C的坐标分别为（4，8），（0，5），过点A作AB⊥x轴于点B，过OB上的动点D作直线y=kx+b平行于AC，与AB相交于点E，连结CD，过点E作直线EF∥CD，交AC于点F。（1）求经过点A，C两点的直线解析式；（2）当点D在OB上移动时，能否使四边形CDEF成为矩形？若能，求出此时k、b的值；若不能，请说明理由；（3）如果将直线AC作向上平移，交Y轴于点Cˊ，交AB于点Aˊ，连结DCˊ，过点E作EFˊ∥DCˊ，交AˊCˊ于点Fˊ，那么能否使四边形CˊDEFˊ成为正方形？若能，请求出此时正方形的面积；若不能，请说明理由。