中考诊断性考试数学试卷
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 总分 |
| 得分 |
一、选择题（本大题共12小题，每小题3分，共36分）
1．05年2月眉山市某一天的天气预报中，洪雅瓦屋山的最低气温是-4℃，仁寿黑龙滩的最低气温是3℃，这一天瓦屋山的气温比黑龙滩的气温低 （ ）
（A）7℃ （B）-7℃ （C）4℃ （D）-1℃
2．用科学记数法记出的2.18×10
所表示的原数为 （ ）
（A）0.00218 （B）0.0218 （C）2180 （D）218000
3．若分式
的值等于零，则x的值为 （ ）
（A）-3 （B）3 （C）±3 (D)9
4.在菱形ABCD中,已知对角线AC=10㎝,BD=6㎝,那么sin
的值等于 ( )
(A)0.86 (B)0.75 (C)0.60 (C)0.51
5.一个容量为60的样本,在整理频率分布时,将所有的频率相加,其和等于 ( )
（A）60 （B）6 （C）1 （D）0.1
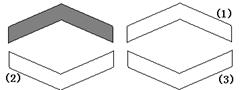6．如图，与阴影部分图形成中心对称的图形是 （ ）
(A)（1）、（2） (B)（2）、（3）
(C)（1）、（3） (C)（1）、（2）、（3）
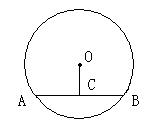7．如图，已知⊙O的弦心距OC等于AB的一半，那么劣弧AB的度数等于
（ ）
（A）45° （B）60° （C）90° （D）120°
8．已知抛物线
经过点（1，4），那么它的对称轴是 （ ）
（A）x=-4 (B)x=4 (C)x=-2 (D)x=2
9.已知
是方程
的两个实数根，则
的值为 （ ）
（A）3 （B）2 （C）1 （D）-1
10．下列各图中的每个大正方形都是由四个边长为1的小正方形组成，其中阴影部分面积为
的是 （ ）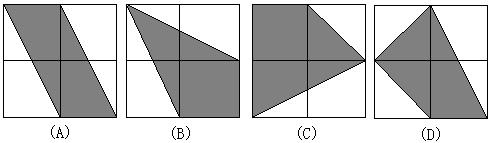
11．已知AB是⊙O的直径，P是AB延长线上一点，PC切⊙O于点C，若PC=3，PB=1，则⊙O的半径等于 （ ）
（A）
（B）4
（C）3 （D）
12．如果方程组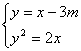
只有一个实数解，那么m的值为 （ ）
（A）
（B）
（C）
（D）
二、填空题（本大题共6小题，每小题4分，共24分）
13．分解因式
14．计算
= （结果中不含负整数指数）
15. 如果两个相似三角形的相似比为5：2，那么它们的周长比为
16．正方形的边长是3，若边长增加x，则面积增加y ,那么y与x之间的函数关系为
17．数据45，44，41，45，43，43，44，42的边准差是 （结果精确到0.01）
18．已知圆锥底面半径为3，高为4，则圆锥的侧面面积等于
三、（本大题共2小题，每小题5分，共10分）
19．计算
20．解不等式
，并把解集在数轴上表示出来
四、（本大题共3小题，每小题7分，共21分）
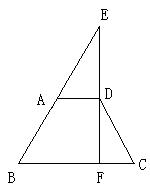
21．如图，在等腰梯形ABCD中，AD∥BC，过D作DF⊥BC，垂足为F，FD的延长线与BA的延长线相交于E，点A为BE的中点.求证：FC=
BF
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数（x） | 中位数 | 众位 |
| 优秀率 |
| 甲组选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 | 8 | 8 | 1．6 | 80％ |
| 乙组选手 | 0 | 0 | 4 | 3 | 2 | 1 |
方差（s
）22．某校初三（1）班分甲、乙两组各选10名学生进行知识抢答赛，共有10道选择体，答对8题（含8题）以上为优秀，各组选手答题结果统计如下：
请完成上表，再根据所学统计知识和表中统计量，从不同方面评价甲、乙两组选手的成绩
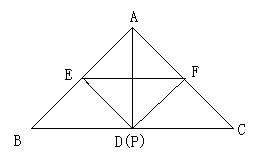
23．如图，将两个等腰直角三角板ABC和DEF叠放在一起，使三角板DEF的直角顶点与三角板ABC的斜边中点P重合，另外两个顶点分别在三角板ABC的边AB、AC上，交EF于O，不添加其他字母，写出图中的一队相似三角形（△ABC与△DEF除外），并加以证明
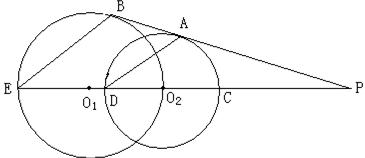24．如图，⊙
经过⊙
的圆心，AB是⊙和⊙的公切线，点A、B为切线，连心线
交AB的延长线于点P，交⊙于点C和D.（1）求证：AD∥BE；（2）设⊙的半径为5，⊙的半径为2，求PA的长.
25．为了有效使用电力资源，某地电力公司从2004年1月起对居民试行“峰谷”用点记费，每天8：00至22：00用点每千瓦时0.56元（“峰电”价），22：00至次日8：00每千瓦时0.28元（“谷电”价），而目前不使用“峰谷”电的居民用电每千瓦时0.53元.
（1）一居民家庭在某月使用“峰谷”电后，付电费95.2元，经测算比不使用“峰谷”电节约10.8，问该家庭当月使用“峰电”和“谷电”多少千瓦时？
（2）当“峰电”用量不超过每月总用电量的百分之几时，使用“峰谷”电比不使用“峰谷”电合算（精确到1％）？
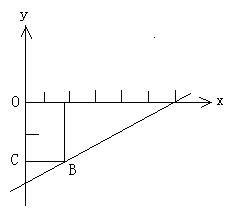
26．如图，在第四象限内的矩形OABC的两边在坐标轴上，一个顶点在一次函数
的图象上，当点A从左向右移动时，矩形的周长面积也随之发生变化，设线段OA的长为m，矩形的周长为L，面积为S.
（1）分别写出L与m ,S与m的函数关系式；
（2）能否求出当m取何值时，矩形的周长L最大？为什么？
（3）矩形的面积是否有最大值？如有最大值，请求出该最大值.