最新初三教学质量检测
数学试卷
| 题号 | 一 | 二 | 三 | 总 分 | |||||||
| 1-8 | 9-12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 得分 | |||||||||||
（说明：本试卷考试时间为90分钟，满分为100分）
一、选择题：（本题共8小题，每题3分，共24分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
每题给出4个答案，其中只有一个是正确的，请把选出的答案编号填在上面的答题表中，否则不给分.
1、下列等式中，错误的是
A、1-(-2)= 3 B、
=2-
C、
＝9 D、
＝3
2、下列等式中，一定成立的是
A、(a-b)2= -(b-a)2 B、
C、x3·x3= x9 D、
3、已知2和-3是关于x的一元二次方程x2 +px +q = 0的两个根，则下列结论错误的是
A、p = -1 B、q= -6
C、△> 0 D、x2 + px +q因式分解为(x -2)(x +3)
4、如图，直线AB∥CD，且∠1=125º，则∠2的值为
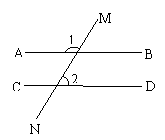A、25º B、55º C、75º D、125º
 |
（4） （5）
5、如图，△ABC中，BD是∠ABC的平分线，DE∥AB交BC于E，已知EC＝3，BE＝2，则AB等于
A、 
B、
C、6
D、4
6、函数y=
的自变量x的取值范围是
A、x≠-1 B、x≠2 C、x<2 D、x≥2
7、下列图形中，是轴对称图形但不是中心对称图形的是
A、平行四边形 B、矩形 C、等腰梯形 D、圆
8、已知⊙O和⊙O'的半径分别为5cm和7cm，且⊙O与⊙O'相切，则圆心距OO'为
A、2cm B、7cm C、9cm D、2cm或12cm
二、填空题：（共4小题，每题3分，共12分，请将答案填入答题表中，否则不给分）
| 题号 | 9 | 10 | 11 | 12 |
| 答案 | （1） （2） |
9、已知x =2， y =3，且xy < 0，则x + y的值为____.
10、因式分解：x3 - 6x2y + 9xy2 =____.
11、正五边形的每一个内角等于____度。
12、为了解全区初三学生数学学习状况，以200名学生的测试成绩作为样本，将他们的成绩整理后分组情况如下：（每组数据含最低值，不含最高值）
| 分组 | ① 40～50 | ② 50～60 | ③ 60～70 | ④ 70～80 | ⑤ 80～90 | ⑥ 90～100 |
| 频数 | 4 | 6 | 60 | n | ||
| 频率 | 0.16 | 0.04 |
（1）n的值为____.
（2）200名学生的测试成绩的中位数落在第___小组内.（填组号即可）
三、解答题：（本部分共8题，其中第13、14、15题每题6分，第16、17题每题8分，第18、19、20每题10分，共64分）
13、化简
-
÷
解：原式=
14、解方程：
解：
15、作图题（要求用直尺和圆规作图，写出作法，保留作图痕迹，不要求写出证明过程.）
已知：线段AB（如图）
求作：一条线段CD，它在线段AB的上方，平行且等于线段AB的二分之一.
作法：
 |
16、已知：在矩形ABCD中，AD＞AB，O是对角线的交点，过O点的一直线MN，分别交BC、AD于M、N.
①求证：梯形MCDN的面积等于矩形ABCD的面积的一半.
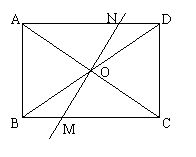②当MN满足什么条件时，将矩形ABCD以MN为折痕，对折后能使C点恰好与A点重合？（只写出满足的条件，不要求证明）
17、请耐心阅读，然后解答后面的问题：“上周末，小明在书城随手翻阅一本高中数学参考书时，无意中看到了几个等式：
sin51ºcos12º + cos51ºsin12º= sin63º
sin25ºcos76º + cos25ºsin76º= sin101º
……………………………………
一个猜想出现在他脑海里，回家后他马上用科学计算器进行验证，发现自己的猜想成立，并能推广到一般. 其实这是大家将在高中学的一个三角函数知识.”
你是否和小明一样也有想法了？下面考考你，看你悟到了什么：
①根据你的猜想填空
sin37ºcos48º + cos37ºsin48º =___________；
sinα cosβ + cosα sinβ = ______________.
②尽管75º角不是特殊角，请你用发现的规律巧算出sin75º的值.
解：
18、小明家距离学校8千米. 今天早晨，小明骑车上学途中，自行车突然“爆胎”，恰好路边有便民服务点. 几分钟后车修好了，他加快速度骑车到校. 我们根据小明的这段经历画了一幅图象，该图描绘了小明行的路程S与他所用的时间t之间的函数关系：
请根据图象，解答下列问题：
①小明行了多少千米时，自行车“爆胎”？修车用了几分钟？
②求修车后小明所行路程S与所用时间t之间的函数关系式（要求写出自变量的取值范围）；
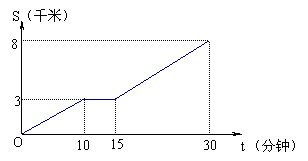③如果自行车未“爆胎”，小明一直用修车前的速度行驶，那么他比实际情况早到或晚到多少分钟（精确到0.1）？
解：
19、如图，已知抛物线y=
(q≠0)与直线y=x交于两点A、B，与y轴交于点C，且OA＝OB，BC∥x轴.
①求p和q的值；
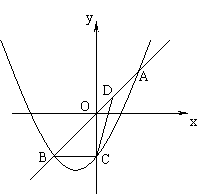②若D是直线AB上的动点，设点D的横坐标为k，△DBC的面积为S，请把S表示为k的函数，并求自变量k的取值范围.
解：
20、如图，AB是的⊙O直径，P是AB延长线上一点，PD切⊙O于点C ，BC和AD的延长线相交于点E，且AD⊥PD
①求证：AB =AE
②当AB : BP为何值时，△ABE是等边三角形？要求说明理由；
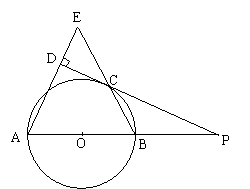③若△ABE是等边三角形，且PC=2，求DE .