初中毕业会考、高级中等学校招生考试数学试卷1
（考试时间：120分钟；满分：150分）
一、填空题（每小题3分，共36分）
1．2的倒数是 .
|
2．在函数
中，自变量
的取值范围是
.
|
= .
|
| |
，那么= .
| |
|
|
7．请你写出一个二次三项式： .
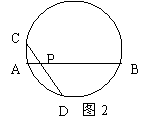
8．如图2，⊙Ο的两条弦AB、CD相交于点P，AP=2，PB=6，CP=3，那么PD= .
9．在比例尺是1：的《中国政区》地图上，量得福州与上海之间的距离为7.5 厘米，那么福州与上海两地实际距离是 千米.
10．如果直线
经过一、二、三象限，那么
O（填上“<”或“>”或“=”）.
11．观察下列各式：1×3=12+2×1，
2×4=22+2×2，
3×5=32+2×3，
… …
请你将猜想到的规律用自然数n（n≥1）表示出来： .
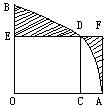12．如图3，扇形AOB的圆心角为直角，正方形OCDE内接于扇形，点C、E、D分别在OA、OB、 
上，过点A作AF⊥ED，交ED的延长线于F，垂足为F。如果正方形的边长为1，那么阴影部分的面积为
。
(图3)
二、选择题（每小题4分，满分32分。每小题都有四个选项，其中只有一个选项的正确的，请把正确的选项的代号写的题末的括号内。）
13.下列运算中，正确的是----------------------------------- （ ）
（A）
（B）
（C） 
（D）
14．不等式组 2x≥4 的解集是-----------------------------------（ ）
x+3>0
（A） x>-3 （B）x≥2 （C）-3<x≤2 （D） x<-3
15．下列各式中属于最简二次根式的是-----------------------------------------------（ ）
（A）
（B）
（C）
（D）
16．下列命题中，真命题的是------------------------------------------------------（ ）
（A） 如果两个角相等，那么这两个角是对顶角
（B） （B）两条对角线相等的四边形是矩形
（C）线段垂直平分线上的点和这条线段两个端点的距离相等
（D）如果两个圆相交，那么这两个圆有三条公切线
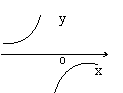
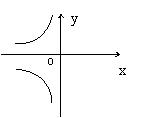
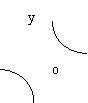
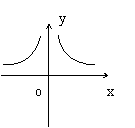17．反比例函数
的图象大致是-- ------------------------------（ ）
（A）
（B）
（C）
（D）
x
18． 已知
、
满足
且
以、为两根的一元二次方程是 （ ）
（A）
（B）
（C）
（D）
19．据《人民日报》2003年6月11日报道，今年1～4月福州市完成工业总产值550亿元，比去年同期工业总产值增长21.46%。请估计去年同期工业总产值在--------（ ）
A.380～400（亿元） B．400～420（亿元） C.420～440（亿元） D.440～460（亿元）
20.如图4，⊙Ο的直径AB垂直于弦CD，垂足为H，点 P是A C上一点（点P不与A、C两点重合）。连结PC、PD、PA、AD，点E在AP的延长线上，PD与AB交于点F。给出下列四个结论：（1）CH2=AH·BH；
（2）
=
（3）AD2=DF·DP；
|
|
其中正确的个数是------------------（
）
|
（A） 1
（B） 2
|
|
|
|
|
（C） 3
（D） 4
 |
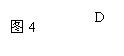三、（第21、22题各7分，第23题6分，24题8分，满分2 8分）
21．计算：
| |
| |
| |
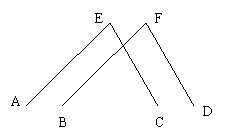
AB=CD，∠D=∠ECA，EC=FD。求证：AE=BF
 |
|
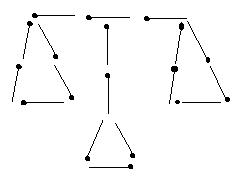23．用若干根火柴棒可以摆出一些优美的图案。如：下图是用火柴棒摆出的一个图案，此图案表示的含义可以是：天平（或公正）.
请你用5根或5根以上火柴棒摆成一个
轴对称图案，并说明你画出的图案的含义.
图案：
含义：
24．甲、乙两名学生进行射击练习，两人在相同条件下各射靶10次，将射击结果作统计分析如下：
| 命中环数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数 | 众数 | 方差 | |
| 甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 | 7 | 6 | 2．2 | |
| 乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
（1）请你填上表中乙学生的相关数据；
（2）根据你所学的统计学知识，利用上述某些数据评价甲、乙两人的射击水平.
四、（满分10分）
25． 为了营造人与自然和谐共处的生态环境，某市近年加快实施城乡绿化一体化工程，创建国家城市绿化一体化城市。某校甲、乙两班师生前往郊区参加植树活动。已知甲班每天比乙班少种10棵树，甲班种150棵树所用的天数比乙班种120棵树所用的天数多2天。求甲、乙两班每天各植树多少棵？
| |
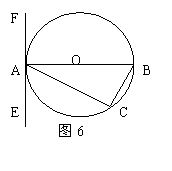
26．已知：三角形ABC内接于⊙О，过 点A作直线EF.
（1）如图6， AB为直径，要使得EF是⊙О的切线，还需添加的条件是（只须写出三种情况）:① 或② 或③ ；
（2）如图 7，AB为非直径的弦，∠CAE=∠B。求证： EF是⊙О的切线.
 |
| |
| | ||||
 | ||||
|
|
|
 | |||||
| |||||
| |||||
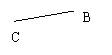六、（满分10分）
27．已知关于的方程
.
（1）
取什么值时，方程有两个实数根；
（2）如果方程的两个实数根
满足
，求的值.
七、（满分12分）
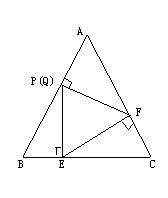
28．已知：如图8，等边三角形ABC中，AB= 2，点P是AB边上的任意一点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC，垂足为E；过点E作EF⊥AC，垂足为F；过点F作FQ⊥AB，垂足为Q。设BP=x，AQ=y。
（1）写出y与x之间的函数关系式；
（2）当BP的长等于多少时，点P与点Q重合；
（3）当线段PE、FQ相交时，写出线段PE、EF、FQ所围成三角形周长的取值范围(不必写出解题过程) .
 |
|
八、（满分12分）
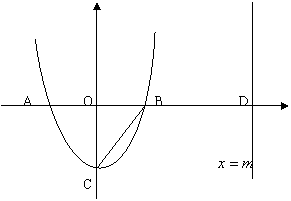
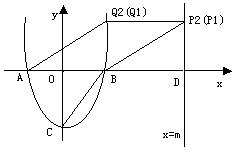
29． 已知：如图9，二次函数
的图象与轴交于A、B两点（点A在点B的左边），与y轴交于点C。直线= m（m >1）与 轴交于点D.
（1）求A、B、C三点的坐标；
|
= m （m > 1）上有一点P (点P在第一象限)，
使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角
|
（3）在（2）成立的条件下，试问：抛物线
上是否存在一点Q，使得四边形
ABPQ为平行四边形？如果存在这样的点Q，请求出m
|
初中毕业会考、高级中等学校招生考试
数学试卷参考答案
一、填空题：（每小题3分，满分36分）
1．
；2.
; 3.a (x+1)2; 4.20; 5.x=2 6.120°;7.略;
8. 4; 9.600; 10.>;
11.n (n+2)=n2+2n; 12.
二、选择题：（每小题4分，满分32分）
13．D；14.B；15.A; 16.C; 17.A; 18.B; 19.D; 20.C
三、（第21、22题各7分，第23题6分、24题8分，满分28分）
21．解原式=3-
+1++1
（5分）
=5 （7分）
22．证明：∵AB=CD
∴AB+BC=BC+CD
即 AC=BD （2分）
在△AEC和△BFD中，
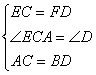
∴△AEC≌△BFD （5分）
∴AE=BF （7分）
23．图案正确 （4分）
说出合理含义 （6分）
24．（1）平均数是7，众数是7，方差是1. 2； 每空得2分 （6分）
（2）根据甲、乙两学生的射击环数、平均数、众数、方差，用一种数据或多种数据进行合理评价，得2分。 （8分）
四、（满分10分）
25．解：设甲班每天植树x棵，那么乙班每天植树（x+10）棵
依题意，得
（5分）
150（x+10）=120x+2x (x+10)
150x+1500=120x+2x2+20x
2x2-10x-1500=0
x2-5x-750=0
(x-30) (x+25)=0
x1=30 x2=-25
经检验知：x1=30 x2=-25都是原方程的解。但x2= -25不符合题意舍去。
∴当x=30时 x+10=40
答：甲班每天植树30棵，乙班每天植树40棵 （10分）
五、（满分10分）
26．（1）参考答案：①：∠CAE=∠B，②AB⊥FE，③∠BAC+∠CAE=90°（或∠BAC与∠CAE互余），④∠C=∠FAB，⑤∠EAB=∠FAB 每空2分 （6分）
（2）证明：连结AO并延长AO交⊙O于H，连结HC
∴∠H=∠B
（7分）
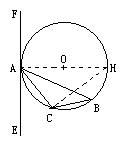
∵AH是直径
∴∠ACH=90°
∵∠CAE+∠HAC=90° （9分）
∴HA⊥EF
∵OA是⊙O的半径
∴EF是⊙O的切线 （10分）
六、（满分10分）
27．解：（1）△=[-（k+1）]2-4（
k2+1）=2k-3
（2分）
∵△
0 即 2k-30，∴k
∴当k时，方程有两个实数根
（2）由∣x1∣=x2
①当x10时 得x1=x2
∴方程有两个相等实数根
∴△=0 即 2k-3=0, k=
又当k=时，有x1=x2=
>0
∴k=符合条件；
②当x1<0时，得x2= -x1
∴x1+x2=0
由根与系数关系得
k+1=0
∴k= -1
由（1）知，与k矛盾，∴k= -1（舍去）
（9分）
综上可得，k=
（10分）
七、（满分12分）
28．解：（1）∵△ABC为等边三解形
∴∠A=∠B=∠C=60°
AB=BC=CA=2
在
中
∵PE⊥BE ∠B=60°
∴∠BPE=30°
而BP=x
∴BE=x
∴EC=2-x
在△CFE中，
∵∠C=60° EF⊥CF
∴∠FEC=30°
∴FC=1-x
（2分）
同理，在△FAQ中可得
AQ=+
x
而 AQ=y，
∴y=+x（0<x
2）；
（4分）
（2）当点P与点Q重合时，有
AQ+BP=AB=2
∴x+y=2 （6分）
∴
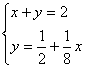解得 x=
∴当BP的长为时，点P与点Q重合； （8分）（3）设三角形的周长为C，得
（12分）
八、（满分12分）
29．解：（1）令y=0，得2x2-2=0，解得，x=
1
点A为（-1，0）、点B为（1，0）；
令x=0，得y=-2，所以点C为（0，-2）； （3分）
（2）①当△PDB∽△COB时
有
∵BD=m-1，OC=2，OB=1
∴
∴PD=2（m-1）
∴P1（m，2m-2） （5分）
②当△PDB∽△BOC时
∵OB=1，BD=m-1，OC=2
∴
∴P2（m，
）
（7分）
（3）假设抛物线y=2x2-2上存在一点Q，使得四边形ABPQ为平行四边形
∴PQ=AB=2 点Q的横坐标为m-2
当点P1为（m，2m-2）时，
点Q1的坐标是（m-2，2m-2） （9分）
∵点Q1在抛物线y=2x2-2图象上
∴2m-2=2(m-2)2-2
m-1=m2-4m+4-1
m2-5m+4=0
m1=1（舍去） m2=4 （10分）
当点P2为（m，）
（11分）
点Q2的坐标是（m-2，）
（11分）
∵点Q2在抛物线y=2x2-2图象上
∴=2（m-2）2-2
m-1=4(m-2)2-4
m-1=4m2-16m+16-4
4m2-17m+13=0
（m-1）（4m-13）=0
∴m3=1（舍去） m4=
∴m的值为4、
（12分）