绝密☆启用前
初中毕业暨升学考试数学试题2
本试卷分第一卷(选择题)和第二卷(非选择题)两部分.第一卷1至2页,第二卷3至8页.满分150分.考试时间120分钟.
第一卷(选择题,共56分)
注意事项:
1.答第一卷前,考生务必用钢笔或圆珠笔在答题卡上填写自己的姓名、准考证号, 然后用铅笔涂准考证号、考试科目代码.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 答案答在试卷上无效. 如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.考试结束,将答题卡和试卷一并交回.
一、选择题(下列各小题的四个选项中,只有一个符合题意.每小题4分,共56分)
1. 9的算术平方根是
A. 81
B. 3
C. ![]() 3
D.
3
D. ![]()
2. 我国人口总数约为13亿,用科学记数法可表示成
A. 13×108 B. 13×109 C. 1.3×109 D. 1.3×1010
3. 下列计算正确的是
A .![]() B.
B.![]()
C.![]() D.
D.![]()
4. 函数![]() 中自变量x 的取值范围是
中自变量x 的取值范围是
A. x≥2 B. x≤2 C.x>2 D.x<2
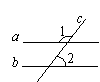 5. 如图,直线a、b被直线c所截,若a//b,∠1=1300 ,则∠2等于
5. 如图,直线a、b被直线c所截,若a//b,∠1=1300 ,则∠2等于
A .300 B. 400
C. 500 D. 600
6. 抛物线y=x2+2x-2的顶点坐标是
A.(2,-2) B.(1,-2) C.(1,-3) D.(-1,-3)
7. 5个正整数从小到大排列,若这组数据的中位数是3,众数是7且唯一,则这5 个正整数的和是
A. 20 B. 21 C. 22 D. 23
8. 如果点(a,-2a)在双曲线![]() 上,则此双曲线的图象在
上,则此双曲线的图象在
A. 第一、二象限 B. 第一、三象限
C. 第二、四象限 D. 第三、四象限
9. 若一个正九边形的边长为a,则这个正九边形的半径是
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
10. 已知一辆小轿车车牌号的后两个数字组成了一个中心对称图形,且这两个数字不相同,则这两个数字的和是
A. 2 B.12 C. 15 D.16
11. 已知关于x的一元二次方程![]() 有两个不相等的实数根,则k的最大整数值是
有两个不相等的实数根,则k的最大整数值是
A. 2 B.1 C. 0 D. -1
12. 在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是
A. B. C. D.
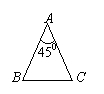
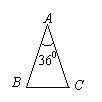 13. 如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是
13. 如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是
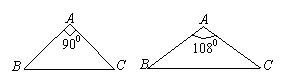 |
(1) (2) (3) (4)
A.(1)(2)(3) B. (1)(2)(4)
C.(2)(3)(4) D. (1)(3)(4)
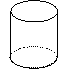
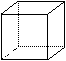
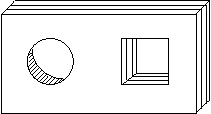 14. 如图是一块带有圆形空洞和
14. 如图是一块带有圆形空洞和
方形空洞的小木板,则下列
物体中既可以堵住圆形空洞,
又可以堵住方形空洞的是
 | |||||
 | |||||
 | |||||
![]()
A. B. C. D.
绝密☆启用前
| 题 号 | 二 | 三 | ||||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | ||
| 得 分 | ||||||||||
江苏省宿迁市2004年初中毕业暨升学考试
数学试题
第二卷(非选择题,共94分)
注意:第二卷共6页.用钢笔或圆珠笔直接在试卷上答题.
| 得分 | 评卷人 |
二、填空题(本题共4小题,每小题4分,共16分)
15. 设(1+x)2(1-x) =a + bx +cx2 +dx3,则a + b +c + d = .
16. 某班在一次考试中,男生的数学平均成绩为118分,女生的数学平均成绩为122分. 若男生人数多于女生人数,则该班数学平均成绩 120分(填“大于”或“等于”或“小于”).
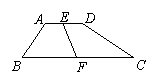 17. 一块长方体橡皮被刀切了3次,最多能被分成 块.
17. 一块长方体橡皮被刀切了3次,最多能被分成 块.
18. 如图,在梯形ABCD中,AD∥BC,∠B +∠C =900,AD=1,
BC =3,E、F分别是AD、BC的中点,则EF= .
三、解答题(解答应写出必要的计算过程、推演步骤或文字说明)
| 得分 | 评卷人 |
19.(本题满分6分)
计算:![]() .
.
| 得分 | 评卷人 |
20.(本题满分6分)
分解因式:![]() .
.
| 得分 | 评卷人 |
21.(本题满分6分)
已知关于x、y的方程组![]() 的解是
的解是![]() ,求
,求![]() 的值.
的值.
| 得分 | 评卷人 |
22.(本题满分8分)
解方程:![]() .
.
| 得分 | 评卷人 |
23.(本题满分8分)
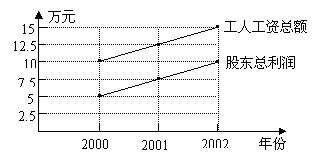 某公司有2位股东,20名工人. 从2000年至2002年,公司每年股东的总利润和每年工人的工资总额如下图所示.
某公司有2位股东,20名工人. 从2000年至2002年,公司每年股东的总利润和每年工人的工资总额如下图所示.
(Ⅰ)填写下表:
| 年 份 | 2000年 | 2001年 | 2002年 |
| 工人的平均工资(元) | 5000 | ||
| 股东的平均利润(元) | 25000 |
(Ⅱ)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?
| 得分 | 评卷人 |
24.(本题满分10分)
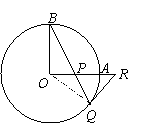
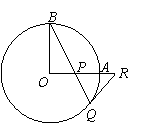 如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R .
如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R .
(Ⅰ)求证:RP=RQ;
(Ⅱ)若OP=PA=1,试求PQ的长.
| 得分 | 评卷人 |
25.(本题满分10分)
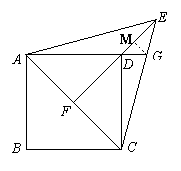
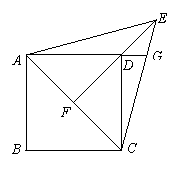 如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连结ED并延长交AC于点F.
如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连结ED并延长交AC于点F.
(Ⅰ)求证:EF⊥AC;
(Ⅱ)延长AD交CE于点G,试确定线段DG和线段DE的数量关系.
| 得分 | 评卷人 |
26.(本题满分12分)
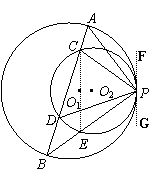
如图(1),已知⊙O1、⊙O2内切于点P,⊙O1的弦AB交⊙O2于C、D两点,连结PA、PC、PD、PB,设PB与⊙O2交于点E.
(Ⅰ)求证:PA·PE=PC·PD;
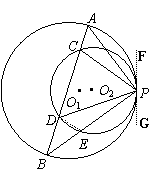
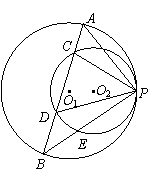 (Ⅱ)若将题中“⊙O1、⊙O2内切于点P”改为“⊙O1、⊙O2外切于点P”,其它条件不变,如图(2),那么(Ⅰ)中的结论是否成立?请说明理由.
(Ⅱ)若将题中“⊙O1、⊙O2内切于点P”改为“⊙O1、⊙O2外切于点P”,其它条件不变,如图(2),那么(Ⅰ)中的结论是否成立?请说明理由.
图(1)
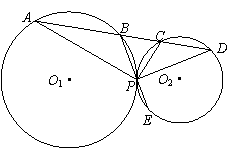 |
图(2)
| 得分 | 评卷人 |
27.(本题满分12分)
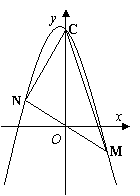
已知抛物线y=-x2+mx-m+2.
(Ⅰ)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB=![]() ,试求m
,试求m
的值;
(Ⅱ)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且 △MNC的面积等于27,试求m的值.
绝密☆启用前
初中毕业暨升学考试
数学试题参考解答及评分标准
说明:
一、解答给出一到两种解法供参考,如果考生的解法与本解答不同,可根据评分标准参照给分.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注的分数,表示正确做到这一步的累计分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题(每小题4分,满分56分)
1、B 2、C 3、B 4、B 5、C 6、D 7、A
8、C 9、D 10、C 11、C 12、D 13、D 14、B
二、填空题(每小题4分,满分16分)
15、0 16、小于(填“< ”给满分 ) 17、 8 18、1
三、解答题
19、(本小题满分6分)
解:原式=6×![]() ………3分
………3分
=![]() ………5分
………5分
=1 ………6分
20、(本小题满分6分)
解法一:
原式=(a3+a2b)-(ab2+b3) ………1分
=a2(a+b)-b2(a+b) ………2分
=(a+b)(a2-b2) ………4分
=(a+b) (a+b) (a-b) ………5分
=(a+b)2(a-b) ………6分
解法二:
原式=(a3-ab2)+(a2b-b3) ………1分
=a(a2-b2)+b(a2-b2) ………2分
=(a2-b2)(a+b) ………4分
=(a+b)(a-b)(a+b) ………5分
=(a-b)(a+b)2. ………6分
21、(本小题满分6分)
解法一:
由已知,得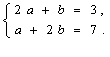 ………2分
………2分
两式相加,得:3a+3b=10 . ………5分
∴a+b=![]() .
………6分
.
………6分
解法二:
由已知,得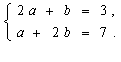 ………2分
………2分
解得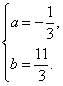 ………5分
………5分
∴![]() .
………6分
.
………6分
22、(本小题满分8分)
解法一:设![]() ,
………1分
,
………1分
则原方程可化为:![]() .
………2分
.
………2分
去分母,并整理得:y2-4y+3=0 . ………3分
解得:y1=1, y2=3 . ………4分
当y1=1时,![]() ,解得
,解得 ![]() ;
;
当y2=3时, ![]() ,解得
,解得 ![]() .
………6分
.
………6分
经检验,x1=![]() ,x2=
,x2=![]() 都是原方程的根. ………8分
都是原方程的根. ………8分
解法二:
去分母,得:x2+3(1-x)2-4x (1-x)=0 . ………2分
化简,得:8x2-10x+3=0 . ………4分
解得:x1=![]() ,x2=
,x2=![]() .
………6分
.
………6分
经检验,x1=![]() ,x2=
,x2=![]() 都是原方程的根. ………8分
都是原方程的根. ………8分
23、(本小题满分8分)
解:(I)
| 年份 | 2000年 | 2001年 | 2002年 |
| 工人的平均工资 | 5000 | 6250 | 7500 |
| 股东的平均利润 | 25000 | 37500 | 50000 |
………4分(说明:每空1分)
(II)设经过x年每位股东年平均利润是每位工人年平均工资的8倍.
由图可知:
每位工人年平均工资增长1250元,
每位股东年平均利润增长12500元 , ………5分
所以 (5000+1250x)×8=25000+12500x. ………6分
解得 x=6 . ………7分
答:到2006年每位股东年平均利润是每位工人年平均工资的8倍. ………8分
 24、(本小题满分10分)
24、(本小题满分10分)
(I)证法一:
连结OQ . ………1分
∵RQ是⊙O的切线,
∴∠OQB+∠BQR=90O . ………2分
∵OA⊥OB,
∴∠OPB+∠B =90O . ………3分
又∵OB=OQ,
∴∠OQB=∠B .
∴∠PQR=∠BPO=∠RPQ . ………4分
∴RP=RQ . ………5分
证法二:
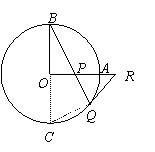 作直径BC,连结CQ . ………1分
作直径BC,连结CQ . ………1分
∵BC是⊙O的直径,
∴∠B+∠C=90O . ………2分
∵OA⊥OB,
∴∠B+∠BPO=90O .
∴∠C=∠BPO . ………3分
又∠BPO=∠RPQ,
∴∠C=∠RPQ.
又 ∵RQ为⊙O的切线,
 ∴∠PQR=∠C .
………4分
∴∠PQR=∠C .
………4分
∴∠PQR=∠RPQ.
∴RP=RQ . ………5分
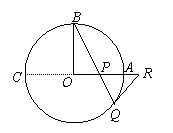
(II)解法一:
作直径AC. ………6分
∵OP=PA=1,
∴PC=3 . ………7分
由勾股定理,得BP=![]() =
=![]() . ………8分
. ………8分
由相交弦定理,得PQ·PB=PA·PC . ………9分
即PQ×![]() =1×3.
=1×3.
∴PQ=![]() .
………10分
.
………10分
解法二:
作直径AE,
过R作RF⊥BQ ,垂足为F . ………6分
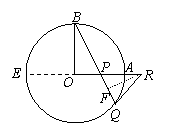 设RQ=RP=x,
设RQ=RP=x,
由切割线定理,得:x2=(x-1)(x+3).
解得:x=![]() .
………7分
.
………7分
又由△BPO∽△RPF得 :
![]() ,
………8分
,
………8分
∴PF=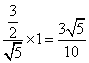 .
………9分
.
………9分
由等腰三角形性质得:PQ=2PF=![]() .………10分
.………10分
 25、(本小题满分10分)
25、(本小题满分10分)
(I)证明:由已知,得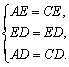
∴△AED≌△CED . ………2分
∴∠AED=∠CED . ………3分
又∵△AEC为等边三角形,
∴EF⊥AC . ………4分
(II)解法一:
过G作GM⊥EF,垂足为M. ………5分
由已知和(Ⅰ) ,得
∠AED=∠CED=30o,∠EAD=150 .
∴∠EDG=45o .
∴MD=GM . ………6分
设GM=x,则DG=![]() .
.
在Rt△MEG中,EG=2MG=2x , ………7分
∴EM=![]() .
………8分
.
………8分
∴ED=![]() +
+![]() =(
=(![]() )
)![]() .
………9分
.
………9分
∴![]() .
.
即DE=![]() DG ( 或
DG ( 或![]() ) .
……10分
) .
……10分
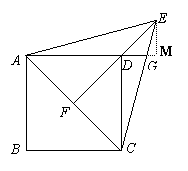 解法二:
解法二:
过E作EM⊥AD,垂足为M. ………5分
在Rt△MDE中,
∵∠EDM=∠MED =45o ,
∴EM=DM .
设EM=DM=x,
则DE=![]() x .
………6分
x .
………6分
在Rt△AEF中,cot300=![]() ,
,
∴DF=AF=![]() .
………7分
.
………7分
∴AD=![]() .
.
=![]() .
………8分
.
………8分
∵△CDG∽△AME ,
∴![]() .
.
即![]() .
.
∴DG=![]() .
………9分
.
………9分
∴![]() .
.
即![]() ( 或
( 或![]() ). ………10分
). ………10分
 26、(本小题满分12分)
26、(本小题满分12分)
(I)证法一:
过点P作⊙O1、⊙O2的公切线FG,
连结CE. ………1分
在⊙O1 中,∠GPB=∠A , ………2分
在⊙O2中,∠GPB=∠ECP , ………3分
∴∠A=∠ECP . ………4分
又∵∠ADP=∠CEP,
∴△ADP∽△CEP . ………5分
∴![]() .
.
即PA·PE=PD·PC . ………6分
证法二:
过点P作⊙O1、⊙O2的公切线FG,
连结DE. ………1分
在⊙O1 中,∠GPB=∠A , ………2分
 在⊙O2中,∠GPB=∠EDP ,
………3分
在⊙O2中,∠GPB=∠EDP ,
………3分
又∵四边形CDEP为⊙O2 的内接四边形,
∴∠ACP=∠DEP . ………4分
∴△ACP∽△DEP . ………5分
∴![]() .
.
即PA·PE=PD·PC . ………6分
(II)结论仍然成立. ………7分
证法一:
过点P作⊙O1、⊙O2的内公切线FG,
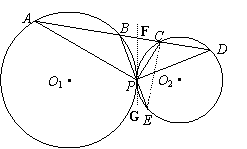 连结CE.
………8分
连结CE.
………8分
在⊙O1 中,∠FPB=∠A ,
在⊙O2中,∠GPE=∠PCE ,
而∠GPE=∠FPB ,
∴∠A=∠PCE . ………10分
又∵∠ADP=∠CEP ,
∴△ADP∽△CEP . ………11分
∴![]() .
.
即PA·PE=PD·PC . ………12分
证法二:
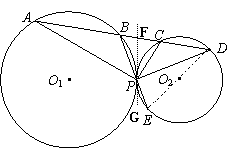 过点P作⊙O1、⊙O2的内公切线FG,
过点P作⊙O1、⊙O2的内公切线FG,
连结DE. ………8分
在⊙O1 中,∠FPB=∠A ,
在⊙O2中,∠GPE=∠PDE ,
而∠GPE=∠FPB ,
∴∠A=∠PDE . ………10分
又∵∠ACP=∠DEP ,
∴△ACP∽△DEP . ………11分
∴![]() .
.
即PA·PE=PD·PC . ………12分
27、(本小题满分12分)
解: (I)设点A(x1,0),B(x2,0) .
则x1 ,x2是方程 x2-mx+m-2=0的两根. ………1分
∵x1 + x2 =m , x1·x2 =m-2 <0 即m<2 ; ………2分
又AB=∣x1 - x2∣=![]() ,
………3分
,
………3分
∴m2-4m+3=0 . ………4分
解得:m=1或m=3(舍去) , ………5分
∴m的值为1 . ………6分
(II)设M(a,b),则N(-a,-b) .
∵M、N是抛物线上的两点,
 ∴
∴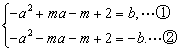 ………7分
………7分
①+②得:-2a2-2m+4=0 .
∴a2=-m+2 . ………8分
∴当m<2时,才存在满足条件中的两点M、N.
∴![]() .
………9分
.
………9分
这时M、N到y轴的距离均为![]() ,
………10分
,
………10分
又点C坐标为(0,2-m),而S△M N C = 27 ,
∴2×![]() ×(2-m)×
×(2-m)×![]() =27 .
…… 11分
=27 .
…… 11分
∴解得m=-7 . ………12分