中考模拟考试数学卷3

中考模拟考试数学卷3

数　学　试　卷

　　　　　　　  (说明：全卷共8页。考试时间为90分钟，满分120分。)

得分	评卷人

　　　　　

一、选择题（本题共5小题，每小题3分，共15分。每小题给出的4个选项中只有一个是正确的，请将所选选项的字母写在题目后面的括号内）

1. 下列式子中错误的是　　　　　　　　　　　　　　　　　　　　　  （　　　 ）.

A.  B.

C.　D.　

2.若单项式与是同类项，则的值是　　　　　  （　　　）.

A. －3 B.－1  C.  D. 3

3. 方程的解是　　　　　　　　　　　　　　　　　　　  （　　　）.

A.  B. 

 C D.　

4. 如图AE、CF是□ABCD的两条高，则图中全等的三角形有　　　　　　　 （　　　）.

A.  2对　　　　　　　　　　　　 

B.  3对　　　　

C.  4对　　　　

D.  5对

	第4题图

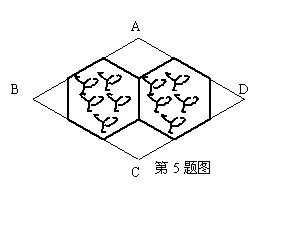5. 菱形花坛ABCD的边长为6cm，∠B=60°，其中由两个正六边形组成的图形部分（图中粗线部分）种花，则种花部分的图形的周长为　　　　　　　　　　　 （　　　）.

A. m　　　　　　　　　　　　　 

B.  20 m　　

C.  22 m　　　　

D.  24 m

得分	评卷人

二、填空题 （本题共5小题，每小题4分，共20分。请将下列各题的正确答案填写在横线上）

6.化简　　　　　　 。

7. 若，则的取值范围是　　　　　　　  。

8. 已知点M在第四象限，则的取值范围是　　　　 。

9. 如图：用四张全等的矩形纸片拼成的图形。请利用图中的空白部分的面积的不同表示方式写出一个关于的恒等式是　　　　　　　　　　  。

 10. 函数中自变量的取值范围是　　　　　 。

得分	评卷人

三、解答题 （本题共5小题，每小题6分，共30分）

11. 计算：

12. 求不等式组 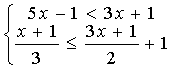的整数解

13. 解方程：

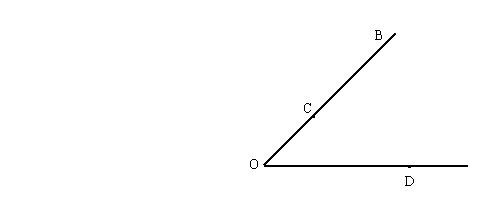
14. 如图：利用直尺和圆规确定一点P，使PC=PD，且点P到∠AOB两边的距离相等。（不写作法和证明，但要保留作图痕迹）

A

　

　　　　　 

15. 某储户存入银行甲、乙两种利息的存款共2万元，甲种存款的年利率是3％，乙种存款的年利率是1.5％，该储户一共得利息525元，试求甲、乙两种存款各是多少？

　　　　　　　　　　　　　　　　　　　  　　　　　 　　　 　　　 　　　

得分	评卷人

四、解答题 （本题共4小题，每小题7分，共28分）

第16题图

16. 如图：等腰梯形ABCD中，AD∥BC，AB=CD，DE⊥BC于E，AE=BE，BF⊥AE于F，请你判断线段BF与图中哪条线段相等，先写出你的猜想，再加以证明

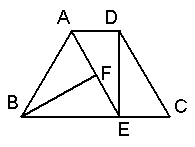
　　　 ①猜想：BF=　　　　  ；

②证明：

17．请用一个 等腰三角形，两个 矩形，三个 圆，在下面三个方框内 各 设计一个轴对称图形，并用简练的文字说明你的创意。

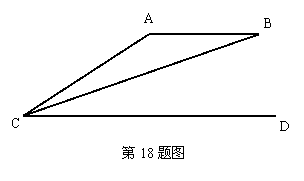
18．美国侦察机B飞抵我国近海搞侦察活动,我战斗机A奋起栏截,地面雷达C测得:当两机都处在雷达的正东方向,且在同一高度时,它们的仰角分别为∠DCA=16°、∠DCB=15°,它们与雷达的距离分别为AC=80km、BC=81km,求此时两机距离是多少km( 精确到0.01km)?

(sin15°=0.26　　cos15°=0.97　　tan15°=0.27　　sin16°=0.28　　cos16°=0.96　　tan16°=0.29)

19．已知一个二次函数的图象经过A(－1，0)、B(3，0)和C(0，－3)三点。

(1)求此二次函数的解析式；

(2)对于实数m，点M(m，－5)是否在此二次函数的图象上？说明理由。

五.解答题.（本题共3小题，每小题9分，共27分）

20．读一读：

式子“1+2+3+…+100”表示从1开始的100个连续自然数的和，由于上述式子比较长，书写不方便，为了简便起见，我们可以将“1+2+3+…+100”表示为，这里“”是求和符号。例如：“1+3+5+…+99”（即从1开始的100以内的连续奇数的和）可以表示为。又如“1³+2³+3³++10³”可表示为。同学们通过对上述材料的阅读，请解答下列问题：

(1)  2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)，用求和符号可表示

为　　　　　　　　　　　　 ；

(2)  计算。

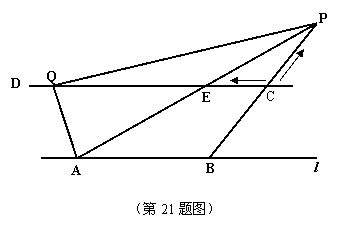
21．如图，A、B是直线l上的两点，AB=4，过l外一点C作CD∥l，射线BC与l所成的锐角∠1=60°，线段BC=2cm，动点P、Q分别从B、C同时出发，P以每秒1cm的速度沿由B向C的方向运动，Q以每秒2cm的速度由C向D的方向运动。设P、Q运动时间为t(秒)，当t>2时，PA交CD于E。

(1)用含t的代数式分别表示CE和QE的代数式；

(2)求△APQ的面积S与t的函数关系式；

(3)当QE恰好平分△APQ的面积时，QE的长是多少？

22．已知：⊙O₁与相交⊙O₂相交于A、B两点，O₁在上⊙O₂，⊙O₂的弦BC切⊙O₁于B，延长B O₁、CA交于点P，PB与⊙O₁交于点D。

(1)求证：AC是⊙O₁的切线；

(2)连接AD、O₁C，求证：AD∥O₁C；

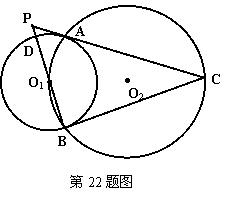(3)如果PD=1，⊙O₁的半径为2，求BC的长。