中考模拟考试数学卷
数 学 试 卷
(说明：全卷共8页。考试时间为90分钟，满分120分。)
| 得分 | 评卷人 |
一、选择题（本题共5小题，每小题3分，共15分。每小题给出的4个选项中只有一个是正确的，请将所选选项的字母写在题目后面的括号内）
1、下列算式中与
是同类二次根式的是（ ）
A 
B 
C 
D 
2、函数
中，自变量x的取值范围是（ ）
A x≥—1 B x≥—1 或x≠2 C x≠2 D x≥—1且x≠2
3、下列算式运算结果正确的是（ ）
A a12÷b6= a2 B （x+y）2=x2+y2 C
D 
4、在Rt△ABC中，∠C=90°，∠A=30°，b=
则此三角形的外接圆的半径是（ ）
A 
B 2
C D 4
5、关于x的一元二次方程（a－1）x2+x+a2－1=0的一个根为0，则a的值为（ ）
A 1 B 2 C 1或－1 D 
| 得分 | 评卷人 |
二、填空题 （本题共5小题，每小题4分，共20分。请将下列各题的正确答案填写在横线上）
6、计算
的结果是_______.
7、如果圆锥母线长60cm，底面直径为6cm，那么这个圆锥的侧面积是_____________.
8、用反证法证明“若⊙O的半径为r，点P到圆心的距离d大于r，则点P在⊙O的外部”时，第一步应假设：_________________.
|
10、锐角△ABC中，AB=AC=6,点D、E在AB、AC上，
AD=4,若△ABC与△ADE相似则线段AE的长
为__________cm
.
| 得分 | 评卷人 |
三、解答题 （本题共5小题，每小题6分，共30分）
11、先化简后在求值：
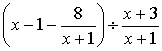其中X=
12、利用数轴求不等式组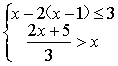
的解集.
13、解分式方程:
14、已知某一次函数的图象与双曲线
交于点(－1,m),且过点(0,1),求该一次函数的解析式
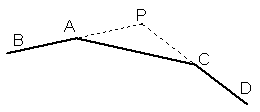
15、如图AB,CD是两条夹角为120°的两条公路,设计时想在拐弯时用一段圆弧弯道把它们连接起来(圆弧在A、C两点和道路连接),测得AC=100m,∠ACP=30°,
（1）在图中画出圆弧形弯道的示意图. （用尺规作图,不写作法但要保留痕迹）
（2）求弯道部分的长(π取3.14,结果保留四个有效数字)
|
四、解答题 （本题共4小题，每小题7分，共28分）
| 得分 | 评卷人 |
16、某地区为了增强市民法制观念,抽调了一部分市民进行了一次知识竞赛,把竞赛成绩(得分取整数)进行整理后分成五组,并绘制成平率分布直方图.请结合图提供的信息解答下列问题.
①抽取了多少名学生参赛?
②60.5～70.5这一分数段的频数,频率分别是多少?
③这次竞赛成绩的中位数落在哪一个分数段内.
17、如图在△ABC中,点E为AC上一点,ED∥BC,EF∥AB,分别交AB、BC与D、F
（1）当∠B= 度时,四边形BFED是矩形.
（2）若AD=4，BD=2，BF=3，则FC= .
（3）如果题设条件不变，当点E 在AC上移动到某一位置满足一定条件时,四边形DBFE是菱形成立。问该结论成立的条件是什么？并证明.
|
证明如下：
18、某灯具店采购了一批某种型号的节能灯共用去400元,在搬运过程中不慎打碎了5盏,该店把余下的灯每盏加价4元全部售出,然后用所得的钱又采购了一批这种节能灯,且进价与上次相同,但购买的数量比上次多了9盏,求每盏灯的进价.
19、如图在△ABC和△DEF中，已知∠A=∠D=70°，∠B=50°，∠E=30°，画直线l，m。使直线l将△ABC分为两个小三角形，使直线m将△DEF分为两个小三角形。使得△ABC分成的两个三角形与△DEF分成的两个小三角形相似，并标出每个小三角形各个内角的度数（画图工具不限，不要求写画法，只要画出一种分法）
|
五、解答题 （本题共3小题，每小题9分，共27分）
| 评卷人 | 得分 |
20、阅读下列材料：
在计算2+5+8+11+14+17+20+23+26+29时，我们发现，从第一个数字开始，后面的每个数与它的前面一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们还可以用下面的公式来计算它的和S；
（其中n表示数的个数，
表示第一个数，
表示最后一个数），那么2+5+8+……+29=
。
用上面的知识解答下面的问题：
某集团总公司决定将下属的一公司对外招商承包，有符合条件的两企业A，B分别拟订上缴利润方案如下：
方案A： 每年结算一次，第一年上缴利润1万元，以后每年比前一年增加1万元。
方案B： 每半年结算一次上缴利润，第一个半年上缴0.3万元，以后每半年比前半年增加0.3万元。
①如果承包4年，你认为应该承包给哪家企业，总公司获利多少？请说明理由。
②如果承包n年，请你分析一下承包给A，B两家企业获利的各种情况。
|
|
|
（2）若AD=
，ED：EA=1：2，求⊙O的半径。
（3）求sin∠CAD
22、如图：有一边长为5cm的正方形ABCD和等腰△PQR，PQ=PR=5cm，QR=8cm，点B、C、Q、R在同一直线l上，当C、Q两点重合时，等腰△PQR以1cm/秒的速度沿直线l按箭头所式方向开始匀速运动，t 秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2，解答下列问题：
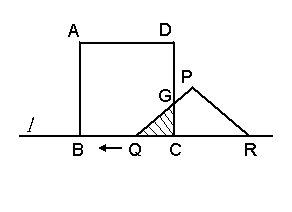（1）当t=3秒时，求S的值；
（2）当t=5秒时，求S的值；
（3）当5≤t≤8时，求S与t
的函数关系式，并求出S的最大值.
数学参考答案
一、选择题（下列各小题的四个选项中，只有一个符合题意。每小题4分，共56分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13* | 13* | 14 |
| 答案 | A | D | D | B | D | C | A | D | B | C | D | C | D | B | A |
二、填空题（4×4＝16分）
15、60° 16、101 17、2 18*、5 18*、32
三、解答题（19—21每题6分，22、23每小题8分，24、25每小题10分，26、27每题）
19、解：原式＝
………………（5分）
＝6 ……………………………………（6分）
20、证明：由正方形ABCD得BC＝DC，∠ABC＝90°…………………（2分）
又∵BG⊥EC ∴△BCG∽△EBG ……………………………………（4分）
∴BE﹕BC＝EG﹕BG 而 BE＝BF ∴BF﹕DC＝EG﹕BG ……（6分）
21、解：设x2－3x＝y ∴ 
∴y2＋5y＋6＝0……………（2分）
∴y1＝－2 y2＝－3 当y1＝－2时，x2－3x＋2＝0得 x1＝1 x2＝2
当y2＝－3时，x2－3x＋3＝0 ，△ ＜0无实数根。…………………… （4分）
经检验x1＝1 x2＝2是原方程的根 ………………………………………（6分）
22*．（1）0元的频数是5，2元的频数是7，5元的频数是21，6元的频数是5，8元的频数是2. ……………………………………………………………（4分）
（2）平均数是4.125，中位数是5，众数是5 （3）5元. ……………（8分）
22*．（1）
；（2）
，
； …………………………………………（4分）
（3）班级人数、三好生数、模范生数、成绩提高奖人数； ……………（6分）
（4）用50个小球，其中3个红球、4个白球、5个黑球，其余均位黄球，把它们装进不透明的口袋中搅均，闭着眼从中摸出一个球，则摸到非黄球的机会就是得到荣誉的机会，摸到红球或白球的机会就是当选为三好生和模范生的机会 ……（8分）
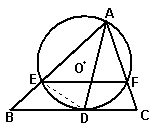23、证明：连结DE，
∵BC是⊙O的切线，∴∠BDE＝∠BAD……………（3分）
∵∠BAD＝∠CAD 而 ∠CAD＝∠DEF……………（6分）
∴∠BDE＝∠DEF ∴EF∥BC …………………（8分）
24*、解：（1）
（每空1分，共4分）
(2)
3x＋3y＝27 
………………………（8分）
x＝5，y＝4；x＝－36，y＝45 (舍去) …………………（9分）
答：两人的速度分别为5千米/小时和4千米/小时。……………（10分）
24*、（略）（1）（3分） （2）（3分） （3）（4分）
25、解：（1）∵△＝4＋16＝20＞0 ∴该抛物线与x轴一定有两个交点。…（5分）
（2）S＝
；………………………………………………………（10分）
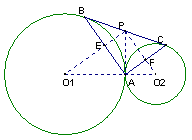
26、证明：（1）过A作两圆的公切线PA交BC于P。
∵BC是两圆的外公切线，
∴PB＝PA＝PC；
∴AB⊥AC；…………………………（5分）
（2）连接P O
，PO
，OO，那么：
PA ⊥OO；∠OPO＝∠ABP＋∠ACP＝90°……………………（7分）
PA2＝AO1×AO2＝2r22 PA＝
r2 ∠ACP＝∠POA……………（9分）
＝tan∠ACP＝tan∠POA＝
…………………………（12分）
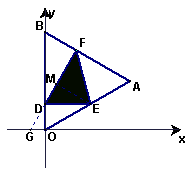
27、解：（1）∵DE∥x轴
∴△ODE为直角三角形，且DE＝EA
设OD＝x,那么OE＝2x，DE＝
∴
, x＝1
∴D(0,1)；E(
,1) ………………………………………………………………（4分）
(2)过E作EM⊥DF于M，延长FD交x轴于G。
∴DM＝
， MF＝ME＝MD＝
∴ DF＝
……………………（7分）
G（
） ∴DF：
……………………………………（9分）
(3) 当D在OB上运动但不与O、B重合时，不能使△DEF成为直角三角形，
理由：∠EDF＝∠A＝60°；∵2∠DEF＝∠AED＜180°∴∠DEF＜90°；
同理∠DFE＜90°∴不能使△DEF成为直角三角形。……………………………（12分）