中考模拟试卷数学试题(一)
数 学 试 题
一、选择题(每小题4分，共40分)
1.计算(-2)3的值是………………………………………………………………………【 】
A.-6 B.6 C.-8 D.8
2.下列运算正确的是……………………………………………………………………【 】
A.(-x2)3=-x6 B.x8÷x4=x2 C.x3+x3=2x6 D.(xy)3=xy3
3.第五次全国人口普查结果显示，我国的总人口已达到13亿人，用科学计数法表示这个数，正确的是…………………………………………………………………………………【 】
A.1.3×108 B.1.3×109 C.0.13×1010 D.13×108
4.一个口袋中有6个白球，6个黑球，下列事件中的必然事件是…………………【 】
A.从口袋中摸出6个球，其中3个白球，3个黑球
B.从口袋中摸出6个球，全部都是黑球
C.从口袋中摸出6个球，全部都是白球
D.从口袋中摸出7个球，至少有一个是白球
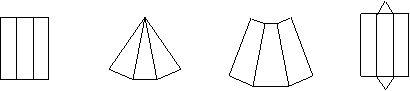5.下面图形中，三棱柱的展开图是…………………………………………………………【 】
A B C D
6.下面抽样合适的是……………………………………………………………………【 】
A.调查某电影院单排号的观众，以了解观众们对所看影片的评价情况
B.为了解植物园一年中游客的人数，小张利用五一长假作了5天的进园人数调查
C.某市为了解在校学生的视力情况，对某重点高中进行抽查
D.某服装厂为了制定某种型号的运动服，到某体校进行抽查
7.已知正比例函数y=(2m-3)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,y1>y2,那么m的取值范围是……………………………………………………………………………………【 】
A.m>
B.m<
C.m>
D.m<
8.
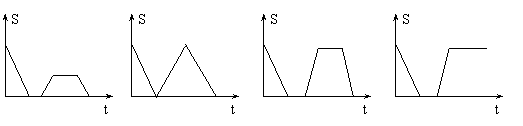有一注满水的游泳池，现按一定的速度将水排尽，然后进行清洗，再将水池注满清水。使用一段时间后，又将水排尽，则游泳池的存水量S(立方米)随时间t(小时)变化的大致图象可以是……………………………………………………………………………………【 】
A B C D
9. 秋千拉绳长3m，静止时踩板离地面0.5m，某小朋友荡该秋千时，秋千在最高处踩踏板离地面2m(左右对称)，则该秋千所荡过的圆弧长为…………………………………【 】
A.πm B.2πm C.
πm D.πm
10.如图，正方形ABCD中，F是AB的中点，E是AD上一点，且AE=
AD，FG⊥CE于G，连结ED、CF，下面四个结论：①△AFE∽△BCF；②FG2=CG·EG；③△EFC∽△EAF；④FE平分∠AFG。其中正确的有………………………………………………………【 】
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分，共20分)
11.小王在商场购买一件降价a元的商品,小王持有该商场的贵宾卡,可以再打九折,结果付了b元,此商品降价前的标价是 元.
12.如果等腰三角形的周长是37,一边是7,则它的腰长是 .
13.某商店举办有奖销售活动,购满100元发对奖券一张,在10000张对奖券中,设一等奖1个,二等奖10个，三等奖100个.若某人购物满100元，那么他中奖的概率是 .
14.若⊙O1的圆心坐标为
，半径为1；⊙O2的圆心坐标为
，半径为3，则这两圆的位置关系是 .
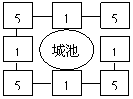15.要在矩形花园中建一条宽a米的道路,如图是一种设计方案.不改变花园中绿化部分的面积,请你在右边的两个矩形中再设计两个不同的方案.
 |
(第15题图) (第16题图)
三、(每小题8分，共16分)
16.岳飞是我国古代宋朝的民族英雄，曾任通泰镇抚史、兼泰州知州。据说在泰州抗击金兵期间，有一次他曾向将领们讲了如下一个布阵图，如图是一座城池，在城池的四周设了八个哨所，一共由24个卫士把守，按直线算，每边都有11个人，后来由由于军情发生变化，连续四次给哨所增添兵力，每次增加4人，但要求在增加人员后，仍然保持每边11个人把守，请问每一次兵力应任何调整？
17.先化简：
，再选取一个合理的数代入求值.
四、(每小题9分，共18分)
18.求不等式组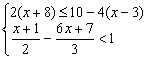
的整数解.
19.如图，直角坐标系中有菱形OABC，若以O为中心，把菱形OABC放大为原来地倍，得菱形OA1B1C1.
(1)在图中画出菱形OA1B1C1.
(2)若∠COA=60°，写出A1、B1、C1的坐标.
五、(每小题10分，共20分)
20.据有关资料统计，两个城市之间每天的电话通话次数T与这两个城市的人口数m、n（单位：万人）以及两城市间的距离d（单位：km）有T＝
的关系（k为常数）．现测得A、B、C三个城市的人口及它们之间的距离如图所示，且已知A、B两个城市间每天的电话通话次数为t，那么B、C两个城市间每天的电话通话次数(用t表示)．
21.我国淡水资源相对紧缺，合理利用水资源有利于我国的长期可持续发展。小明记录了他家6—12月每月月初水表的读数及所交水费(如下表)
| 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 水表止码(m3) | 2234 | 2244 | 2257 | 2268 | 2280 | 2292 | 2304 |
| 所交水费(元) | 24.16 | 15.10 | 19.63 | 16.61 | 18.12 | 18.12 | 18.12 |
请你利用所学的统计知识，解答下列问题：
(1)小明家2004年大约共用水多少立方米？
(2)若小明家2005年的用水量计划比2004年的用水量下降10%，问2005年小明家的水费需要多少元？
六、(本题满分12分)
22.某工厂生产某种产品，每件产品的出厂价为1万元，其原料成本价（含设备损耗等）为
0.55万元，同时在生产这程中平均每生产一件产品有1吨的废渣产生，为达到国家环保要求
需要对废渣进行脱硫，脱氮等处理，现有两种方案供选择
方案一：由工厂对废渣直接进行处理，每处理1吨废渣所用的原料费为0.05万元，并且每月设备维护及损耗费为20万元。
方案二：工厂将废渣集中到废渣处理厂统一处理，每处理1吨废渣需付0.1万元的处理费。
问：（1）工厂每月生产x件产品，每月利润为y万元，分别求出方案一和方案二处理废渣时，y与x之间的函数关系式（利润＝总收入—总支出）
（2）若你作为工作负责人，如何根据月生产量选择处理方案，既可达到环保要求又最
合算？
七、(本题满分12分)
23.
如图，P是正方形ABCD内一点，PA=a，PB=2a，PC=3a.将△APB绕点B按顺时针方向旋转，使AB与BC重合，得△CBP′.
(1)求证：△PBP′是等腰直角三角形；
(2)猜想△PCP′的形状，并说明理由；
(3)求∠APB的度数.
八、(本题满分12分)
24.抛物线y=ax2+(a+m)x-
m与x轴相交于A(1，0)、B（x2，0）两点，交y轴正半轴于点C，且S△ABC=.
(1)求x2的值；
(2)求此抛物线的解析式；
(3)在抛物线上(在B点的右侧)是否存在一点P，使∠PCB=∠CBA-∠ACB？若存在，求过C、P两点的直线解析式；若不存在，请说明理由.