中考适应性考试数学卷
数 学 试 卷
本试卷分第一卷（选择题）和第二卷（非选择题）两部分，第一卷1至2页，第二卷3至8页，满分150分，考试时间120分钟。其中重复题号的前一题为人教版内容题，后一题为华师大版内容题，重复题号的试题请同学们任意选做一题，多做不加分。
第一卷（选择题，共56分）
一、选择题（下列各小题的四个选项中，只有一个符合题意。每小题4分，共56分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13* | 13* | 14 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1．sin30°的值等于……………………………………………………………………（ ）
A.
B.
C.
D.1
2．若
，则
的值为 …………………………………………………（ ）
A.－2
B.0 C.2
D.
3．某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案，你认为符合条件的是（ ）
A.正三角形 B.正五边形 C.等腰梯形 D.菱形
4．如图，∠1=∠2，则下列结论一定成立的是………………………………………（ ）
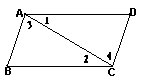A.AB∥CD
B.AD∥BC
C.∠B=∠D D.∠3=∠4
5．以下不能构成三角形的三边长的数组是 ……………………………………………（ ）
A.（1,
,2） B.（,
,
） C.（3，4，5）
D.（32，42，52）
6．下面式子从左边到右边的变形中是因式分解的是 ………………………………（ ）
A.
B.
C.
D.
7．顺次连接平行四边形四边中点所得的四边形是 ………………………………（ ）
A.平行四边形 B.矩形 C.菱形 D.正方形
8．若
，则
的取值范围是 …………………………
（ ）
A.
B.
C.
D.
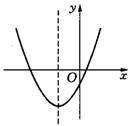
9．如图为二次函数
的图象，则一次函数
的图象不经过（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
（第9题） （第10题）
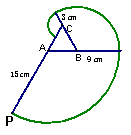
10．如图，有一个边长为6cm的正三角形木块ABC，点P是CA延长线上的一点，在A、P之间拉一条长为15cm细丝，握住点P，拉直细线，把它全部紧紧绕在△ABC木块上（缠绕时木块不动），则点P运动的路线长为 ………………………………………（ ）
A.9πcm B.12πcm C.18πcm D.24πcm
11．已知一组数据为：3，4，5，6，6，6，7，8，9.其中平均数、中位数和众数的大小关系是： ………………………………………………………………………………（ ）
A.平均数＞中位数＞众数 B.平均数＜中位数＜众数
C.中位数＜众数＜平均数 D.众数＝中位数＝平均数
12．两圆半径长分别为R和r，两圆心距为d，以长度为R、r、d的三条线段首尾相接可以围成一个三角形，则两圆的位置关系是 ……………………………………（ ）
A.外离 B.相切 C.相交 D.内含
13*．（人教版）要使二次三项式
在整数范围内能进行因式分解，那么整数p的取值可有 …………………………………………………………………………（ ）
A.2个 B.4个 C.6个 D.无数个
 |
13*．（华师版）在使用科学计算器时依次按下列键
后，会得到下列那个结果（说明： 表示第二功能键） …………………………………… （ ）
A.
B.
C.
D.
14．方程
的正根的个数为 ……………………………………………（ ）
A.0个 B.1个 C.2个 D.3个
第二卷（非选择题，共94分）
| 得分 | 评卷人 |
|
|
|
二、填空题（4×4＝16分）
15．以半圆为侧面的圆锥体的锥角等于 0.
16．观察数列：2，5，10，17，26，……，根据规律，其中第十个数是 .
17．已知m、n是方程x2－2003x＋2004＝0的两个根，则(n2－2004n＋2005)与(m2－2004m＋2005)的积是 .
18*．（人教版）把(x2－x＋1)2展开得a4x4＋a3x3＋a2x2＋a1x＋a0，那么a4＋a2
＋a0＝ .
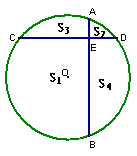18*．（华师版）如图所示AB、CD是⊙O的两条弦，且AB⊥CD于E，O到AB、CD的距离分别为2和4，则S1＋S2－S3－S4＝ .
三、解答题
| 得分 | 评卷人 |
|
|
|
19．（本题满分6分）
计算：
| 得分 | 评卷人 |
|
|
|
20．（本题满分6分）
如图，正方形ABCD中，BE＝BF，BG⊥EC，
求证：BF︰DC＝EG︰BG．
| 得分 | 评卷人 |
|
|
|
21．（本题满分6分）
解方程： 
| 得分 | 评卷人 |
|
|
|
22*．（人教版：本题满分8分）
夏雪同学调查了班级同学身上有多少零用钱，将每位同学的零用钱记录下来，下面是全班40名同学的零用钱的数目（单位：元）
2，5，0，5，2，5，6，5，0，5，5，52，5，8，0，5，5，2，5，
5，8，6，5，2，5，5，2，5，6，5，5，0，6，5，6，5，2，5，0.
（1）请你写出同学的零用钱（0元，2元，5元，6元8元）出现的频数；
（2）求出同学的零用钱的平均数、中位数和众数；
（3）假如老师随机问一个同学的零用钱，老师最有可能得到的回答是多少元？
| 得分 | 评卷人 |
|
|
|
22*．（华师版：本题满分8分）
某校每学期都要对优秀的学生进行表扬，每班采取民主投票的方式进行选举，若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额，且各项均不能兼得，现在学校有30个班级，平均每班50人。
（1）作为一名学生，你恰好能得到荣誉的机会有多大？
（2）作为一名学生，你恰好能当选三好生或模范生的机会各有多大？
（3）在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中，哪些是解决上面两个问题所需要的？
（4）你可以用哪些方法来模拟实验？（举出一例加以说明）
| 得分 | 评卷人 |
|
|
|
23．（本题满分8分）
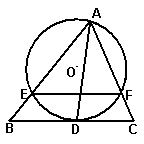已知△ABC中，∠A的平分线AD交BC于D，⊙O过点A，且和BC切于D，和AB、AC分别交于E、F.
求证：EF∥BC
| 得分 | 评卷人 |
|
|
|
24*．（人教版：本题满分10分）
甲、乙两人分别从相距27千米的A、B两地同时出发相向而行，3小时后相遇，相遇后两人按原来的速度继续前进，甲到达B地比乙到达A地早1小时21分，求两人的速度。
（1）设甲的速度是x千米/小时，乙的速度是y千米/小时，根据题意，利用速度、时间、路程之间的关系填写下表（要求用适当的代数式，完成表格）：
|
| 速度（千米/时） | 所用时间（时） | 所走的路程（千米） | |
| 相遇时 | 甲 | x | 3 |
|
| 乙 | y | 3 |
| |
| 走完全程时 | 甲 | x |
| 27 |
| 乙 | y |
| 27 | |
（2）列出方程（组），并求出问题的解。
| 得分 | 评卷人 |
|
|
|
24*．（华师版：本题满分10分）
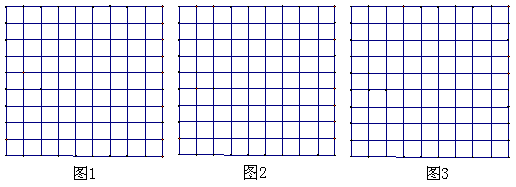
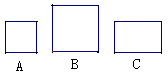现有足够的2×2，3×3的正方形和2×3的矩形图片A、B、C，如图所示，从中各选取若干个图片拼成不同的图形。请你在下面给出的方格纸中，按下面的要求分别画出一种示意图（说明：下面给出的方格纸中，每个正方形的边长为1。拼出的图形，要求每两片之间无缝隙，也不重叠。画图必须保留拼图的痕迹）：
（1）选取A、B型各1片，C型2片，在图1中拼成一个正方形。
（2）选取A型4片，B型1片，C型4片，在图2中拼成一个正方形。
（3）选取A型3片，B型1片，C型若干，在图3中拼成一个矩形。
| 得分 | 评卷人 |
|
|
|
25．（本题满分10分）
已知抛物线
（1）求证：该抛物线与x轴一定有两个交点；
（2）若该抛物线与x轴的两个交点分别为A、B，且它的顶点为P，求△ABP的面积。
| 得分 | 评卷人 |
|
|
|
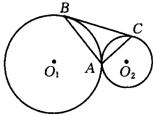
26．（本题满分12分）
已知，如图⊙O
与⊙O
外切于点A，BC是⊙O和⊙O的公切线，B、C为切点。
（1）求证：AB⊥AC；
（2）若
、
分别为⊙O、⊙O的半径，且＝2
，求
的值。
| 得分 | 评卷人 |
|
|
|
27．（本题满分12分）
如图，△OAB是边长为
的等边三角形，其中O是坐标原点，顶点B在Y轴的正半轴上，将△OAB折叠，使点A落在边OB上，记为D，折痕为EF。
（1）当DE∥X轴时，求点D和E的坐标
（2）当DE∥X轴时，求线段DF的长及直线DF的解析式；
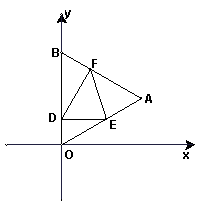（3）当D在OB上运动但不与O、B重合时，能不能使△DEF成为直角三角形？若能，请求出此时点D的坐标：若不能，请你说明理由。