新课标(北师大版)中考数学第一轮综合测试卷
一、选择题(每小题4分，共40分)
1、实施西部大开发战略是党中央面向21世纪的重大决策，西部地区占我国国土面积的
，我国国土面积约960万平方千米，用科学记数法表示我国西部地区的面积为（ B ）
A.64×105km2 B.6.4×106km2 C.6.4×107km2 D.640×104km2
2、下列计算中，正确的是（ D ）
A．2a+3b=5ab B．a·a3=a3 C．a6÷a2=a3 D．(-ab)2=a2b2
3、
……，依次观察左边三个图形，并判断照此规律从左到右第四个图形是（ B ）
4、不等式x－2＜0的正整数解是( A ).
A.1 B.0，1 C.1，2 D.0，1，2
5、衡量样本和总体的波动大小的特征数是（ B ）
A.平均数 B.方差 C.众数 D.中位数
6、某初中毕业班的每一个同学都将自己的相片向全班其他同学各送一张表示留念，全班共送了2550张相片，如果全班有x名学生，根据题意，列出方程为（ D ）
A.x（x＋1）＝2550 B.x（x－1）＝2550
C.2x（x＋1）＝2550 D.x（x－1）＝2550× 2
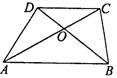7、如图，梯形ABCD的对角线交于点O，有以下四个结论：①△AOB∽△COD；②△AOD∽△ACB；③S△DOC∶S△AOD=DC∶AB；④S△AOD=S△BOC.其中始终正确的是（ C ）
A.①②③ B.①②④ C.①③④ D.②③④
8、已知在直角坐标系中，以点A(0，3)为圆心，以3为半径作⊙A，则直线y=kx+2(k≠0)与⊙A的位置关系是( B )
A.相切 B.相交 C.相离 D.与k值有关
9、用一把带有刻度的直角尺，
①可以画出两条平行的直线a与b，如图（1）；
②可以画出∠AOB的平分线OP，如图（2）；
③可以检验工件的凹面是否成半圆，如图（3）；
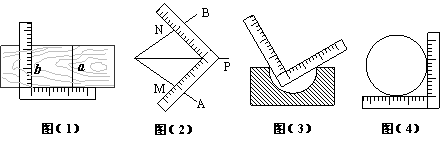④可以量出一个圆的半径，如图（4）.
|
上述四个方法中，正确的个数是（ D ）
A.1个 B.2个 C.3个 D.4个
10、甲、乙、丙三位同学进行立定跳远比赛，每人轮流跳一次称为一轮，每轮按名次从高到低分别得3分、2分、1分(没有并列名次)，他们一共进行了五轮比赛，结果甲共得14分；乙第一轮得3分，第二轮得1分，且总分最低.那么丙得到的分数是( B )
A. 8分 B. 9分 C. 10分 D.11分
二、填空题(每小题4分，共40分)
11、不等式组
的整数解是
-
<x<
.
12、一个口袋中装有 4个白球，1个红球，7个黄球，搅匀后随机从袋中摸出 1个球是白球的概率是 
.
13、某城市自来水收费实行阶梯水价，收费标准如下表所示，用户5月份交水费45元，则所用水为 20 度.
| 月用水量 | 不超过12度的部分 | 超过12度不超过18度的部分 | 超过18度的部分 |
| 收费标准（元/度） | 2.00 | 2.50 | 3.00 |
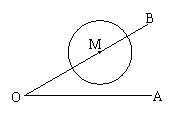14、如右图，已知∠AOB=30°，M为OB边上一点，以M为圆心、2cm为半径作M. 若点⊙M在OB边上运动，则当OM= 4 cm时，⊙M与OA相切.
15、将一个底面半径为3cm，高为4cm的圆锥形纸筒沿一条母
线剪开，所得到的侧面展开图的圆心角度数为__216°______.
三、(每小题8分，共16分)
16、先化简
，再请你自选一个合理的值，求原式的值.
17、已知一次函数y=kx+m与反比例函数y=
的图象在第一象限内的交点为P(1，3).
(1)求这两个函数的解析式；
(2)在所给坐标系中画出它们的图象，并根据图象写出x>0时，一次函数的值小于反比例函数的值的x的取值范围.
(1)y=x+2 y=
(2)图略 0<x<1.
四、(每小题9分，共18分)
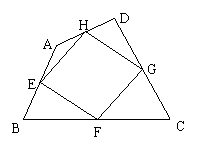
18、如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由．
解：添加的条件：
理由：
条件：对角线相等；理由略.
19、某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要完成总面积为80m2的三个项目的任务，三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示：
（1）从上述统计图中可知：每人每分钟给擦课桌椅 m2；擦玻璃、擦课桌椅、扫地拖地的面积分别是 m2， m2， m2；
（2）如果x人每分钟擦玻璃的面积是ym2，那么y关于x的函数关系式是 ；（3）他们一起完成扫地和拖地的任务后，把这13人分成两组，一组去擦玻璃，一组去擦课桌椅。如果你是卫生委员，该如何分配这两组的人数，才能最快地完成任务。
 |
(1)
16 20
44 (2)y=
x (3)应分配8人去檫玻璃，5人去檫课桌椅.
五、(每小题10分，共20分)
20、根据下图给出的信息，求每件T恤衫和每瓶矿泉水的价格.
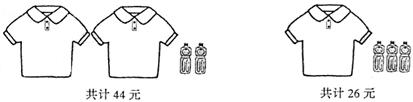
每件T恤衫20元，每瓶矿泉水2元.
21、已知二次函数y=x2-2mx+m2-m-2的图象的顶点为C，图象与x轴有两个不同的交点A、B，其坐标为A（x，0）、B（4，0），且△ABC的面积为8。求这个二次函数的解析式。
由B点坐标为（4，0）得：
16－8m+m2－m－2=0 ∴ m1=2 m2=7
当m=2时，y=x2-4x
△ABC面积为8，符合题意
当m=7时，y=x2-14x+40
∴点A（10，0） B（4，0） 顶点C（7，－9）
∴△ABC的面积为27，不符合题意
∴函数解析式为y=x2-4x
六、(本题12分)
22、小芳和小亮两人进行掷骰子游戏。小芳的骰子六个面中有两个面是红色，其余面是黄、蓝、白、黑。小亮的骰子六个面中分别是红、黄、蓝、白、黑、紫，规则是各自掷自己的骰子。向上的颜色相同小芳得分，否则小亮得分，这个游戏对双方公平吗？说明理由。如果不公平，怎样修改游戏规则才能使双方公平？
不公平；因为小芳获胜的概率为
，小明获胜的概率为
。
七、(本题12分)
23、某中学为筹备校庆活动，准备印刷一批校庆纪念册，该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表
| 印数a(单位：千册) | 1≤a＜5 | 5≤a≤10 |
| 彩页(单位：元/张) | 2.2 | 2.0 |
| 黑白页(单位：元/张) | 0.7 | 0.6 |
(1)印制这批纪念册的制版费为 元；
(2)若印制2千册，则共需多少费用？
(3)如果该校希望印数至少为4千册，总费用至多为60000元，求印数的取值范围(精确到0.01千册).
(1)1500元 (2)(2.2×4+0.7×6)×2000+1500=27500(元) (3)符合要求的印数x(千册)的取值范围为：4≤x≤4.5或5≤x≤5.04
八、(本题12分)
24、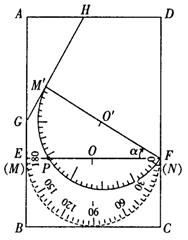
如图，在矩形ABCD中，AB=3，AD=2，点E、F分别在AB、DC上，AE=DF=2。现把一块直径为2的量角器(圆心为O)放置在图形上，使其0°线MN与EF重合；若将量角器0°线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α(0°<∠α<90°)，此时量角器的半圆弧与EF相交于点P，设点P处量角器的读数为n°.
(1)用含n°的代数式表示∠α的大小；
(2)当n°等于多少时，线段PC与M′F平行？
(3)在量角器旋转过程中，过点M′作GH⊥M′F，交AE于点G，交AD于点H。设GE= x，△AGH的面积为S，试求出S与x的函数关系式，并写出自变量x的取值范围.
(1)∠α=90°-n° (2)n°=120° (3)S=
，0<x<2