新课标[北师大版]第一轮复习测试卷
一、选择题(每小题4分，共40分)
1、(-3)2与-32 （ B ）
A.相等 B.互为相反数 C.互为倒数 D.它们的和为18
2、下列各式计算正确的是（ D ）
A.(a5)2=a7 B.2x―2=
C.4a3·2a2=8a6 D.a8÷a2=a6
3、已知一次函数y=kx+b的图象如图所示，则（ B ）
A.k>0，b<0 B.k>0，b>0 C.k<0，b<0 D.k<0，b>0
 | |||||
 | |||||
 | |||||
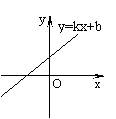(第3题图) (第4题图) (第5题图)
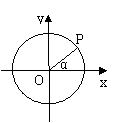
4、如图，以直角坐标系的原点O为圆心，1为半径作圆.若点P是该圆上第一象限内的一点，且OP与x轴正方向组成的角为α，则点P的坐标是（ D ）
A. (cosα，1) B. (1，sinα) C.（sinα，cosα） D. (cosα，sinα)
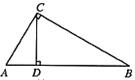
5、如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AC=6，AB=9，则AD的长是（ C ）
A.6 B.5 C.4 D.3
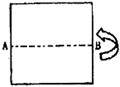
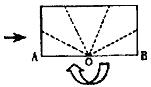
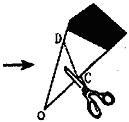
6、如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形）.则∠OCD等于（C ）
A．108° B．144° C．126° D．129°
7、甲做实验“估计一个啤酒瓶盖抛起后落地时开口朝上的概率有多大”，下列说法中合理的是( D )
A.口朝上、开口朝下都有可能，无规律可找
B.抛20次开口朝上8次，则可得出开口朝上的概率约为40%
C.多人分组实验，若啤酒瓶盖不够，可暂时用可乐瓶盖代替，这样数据合起来可缩短实验时间
D.在相同条件下，实验次数越多，估计值越准确
8、若⊙O1的圆心坐标为(2，0)，半径为1；⊙O2的圆心坐标为(-1，0)，半径为3，则这两圆的位置关系是（ A ）
A. 相交 B. 相切 C. 相离 D. 内含
9、已知A=A0(1+mt)(m、A、A0均不为零)，则t=（ D ）
A.
B.
C.
D.
10、如图，等腰直角三角形ABC（∠C=Rt∠）的直角边长与正方形MNPQ的边长均为4cm，CA与MN在直线l上，开始时A点与M点重合；让△ABC向右平移；直到C点与N点重合时为止。设△ABC与正方形MNPQ的重叠部分（图中阴影部分）的面积为ycm2，MA的长度为xcm，则y与x之间的函数关系大致是（ B ）
A B C D
二、填空题(每小题4分，共20分)
11、已知正比例函数y=(3k-1)x，若y随x的增大而增大，则k的取值范围是 k>
.
12、直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积是 30 cm2.
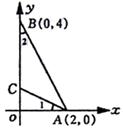
13、如图，已知两点A（2，0）、B（0，4），且∠1=∠2，则点C的坐标是 (0，1) .
14、为了能有效地使用电力资源,我市供电部门最近进行居民峰谷用电试点，每天8:00至21:00用电每千瓦时0.55元（“峰电”价），21:00至次日8:00每千瓦时0.30元(“谷电”价)．王老师家使用“峰谷”电后,五月份用电量为300千瓦时，付电费115元，则王老师家该月使用“峰电” ___100___千瓦时.
15、根据指令[s,A]（s≥0, 0°≤A<360°）机器人在平面上能完成如下动作：先在原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s. 现在机器人在平面直角坐标系的原点，且面对y轴的负方向，为使其移动到点（-3，3），应下的指令是
[3
，225°] .
三、(每小题8分，共16分)
16、解不等式组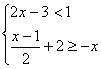
，并把解集在数轴上表示出来。
-1≤x<2
17、如图，平面直角坐标系中画出了函数y=kx+b的图象.
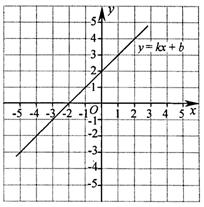(1)根据图象，求k、b的值；
(2)在图中画出 函数y= -2x+2的图象；
(3)求x的取值范围，使函数y=kx+b的函数值大于y= -2x+2的函数值.
(1)k=1，b=2 (2)图略 (3)x>0
四、(每小题9分，共18分)
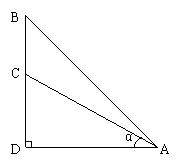18、如图，在坡角α为30°的山顶C上有一电视塔，在山脚A处测得电视塔顶部B的仰角为45°，斜坡AC长为40米，求电视塔BC的高.
BC=200(
-1)米
|
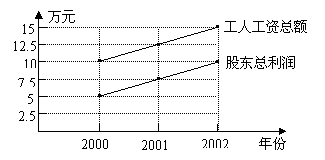20、某公司有2位股东，20名工人. 从2000年至2002年，公司每年股东的总利润和每年工人的工资总额如下图所示.
（Ⅰ）填写下表：
| 年 份 | 2000年 | 2001年 | 2002年 |
| 工人的平均工资（元） | 5000 | ||
| 股东的平均利润（元） | 25000 |
（Ⅱ）假设在以后的若干年中，每年工人的工资和股东的利润都按上图中的速度增长，那么到哪一年，股东的平均利润是工人的平均工资的8倍？
(I)
| 年份 | 2000年 | 2001年 | 2002年 |
| 工人的平均工资 | 5000 | 6250 | 7500 |
| 股东的平均利润 | 25000 | 37500 | 50000 |
（II）设经过x年每位股东年平均利润是每位工人年平均工资的8倍.由图可知：
每位工人年平均工资增长1250元，
每位股东年平均利润增长12500元 ，
所以 （5000＋1250x）×8＝25000＋12500x. 解得 x＝6 .
答：到2006年每位股东年平均利润是每位工人年平均工资的8倍.
五、(每小题10分，共20分)
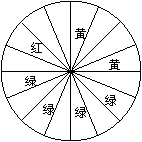
20、某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：顾客每购买100元的商品，就可以获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得100元、50元、20元的购物券(转盘被等分成16个扇形).
(1)如果小明妈妈购物176元，她获得购物券的概率是多少？她得到100元，50元，20元购物券的概率分别是多少？
(2)如果购物150元以上可以直接返还20元购物券，你认为怎样选择比较合算？
(1)P(获得购物券)=
，P(获得100元购物券)=
，P(获得50元购物券)=
，P(获得20元购物券)=
.
(2)转动一次转盘平均得购物券100×+50×+20×=17.5(元)<20(元)，所以直接返还20元购物券较合算.
21、如图，在等腰梯形ABCD中，AB∥CD，AC、BD是对角线，将△ABD沿AB向下翻折到△ABE的位置，试判定四边形AEBC的形状，并证明你的结论．
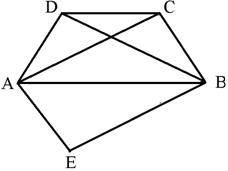
四边形AEBC是平行四边形。证明略.
六、(本题满分12分)
22、已知：射线OF交⊙O于点B，半径OA⊥OB，P是射线OF上一个动点(不与O、B重合)，直线AP交⊙O于点D，过D作⊙O的切线交射线OF于点E.
(1)图a 是点P在圆内移动时符合已知条件的图形，请你在图b中画出点P在圆外移动时符合已知条件的图形；
(2)观察图形，点P在移动过程中，△DPE的边、角或形状存在某些规律，请你通过观察、测量、比较，写出一条与△DPE的边、角或形状有关的规律；
(3)在点P移动过程中，设∠DEP的度数为x，∠OAP的度数为y，求y与x的函数关系式，并写出自变量x的取值范围.
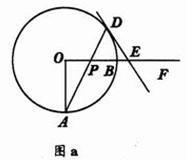
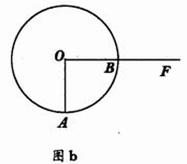
(1)图略 (2)∠EDP=∠DEP或PD=PE或△PDE是等腰三角形 (3)y=
x，0°<x<180°，且x≠90°.
七、(本题满分12分)
23、已知抛物线y=2x2+bx-2 经过点A（1，0）.
(1)求b的值；
(2)设P为此抛物线的顶点，B（a ,0）（a≠1）为抛物线上的一点，Q是坐标平面内的点。如果以A、B、P、Q为顶点的四边形为平行四边形，试求线段PQ的长。
 |
（1）由题意得2×12+b×1-2=0 ∴b=0
(2)由（1）知y=2x2-2 ∴抛物线的顶点为（0，-2）
∵B（a,0）(a≠1)为抛物线上的点，∴2a2-2=0 解得a1=-1,a2=1（舍去）
∴B(-1,0) 符合题意的Q点在坐标平面内的位置有下述三种：
①当Q在y轴上时, ∵四边形QBPA为平行四边形，可得QO=OP=2，∴PQ=4
②当点Q在第四象限时，∵四边形QBPA为平行四边形，∴PQ=AB=2
③当点Q在第三象限时，同理可得PQ=2。
八、(本题满分12分)
24、如图，四边形ABCD中，AC=6，BD=8且AC⊥BD顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……，如此进行下去得到四边形AnBnCnDn .
（1）证明：四边形A1B1C1D1是矩形；（6分）
（2）写出四边形A1B1C1D1和四边形A2B2C2D2的面积；（2分）
（3）写出四边形AnBnCnDn的面积；（2分）
（4）求四边形A5B5C5D5的周长.（4分）
(1)证明略（2）四边形
的面积为12；四边形
的面积为6； （3）四边形
的面积为
；（4）∴矩形
的周长=