初 三 数 学(第35周)
主讲教师:孙开华
主审教师:陈云楼
【教学内容】
相似形
【教学目标】
1、掌握比例的基本性质定理、合比性质和等比性质,会用它们进行简单的比例变形,会判断四条线段是否成比例,了解黄金分割。
2、了解平行线分线成比例定理及截三角形两边或其延长线的直线平行于第三边的判定定理的证明,会用它们证明线段成比例、线段平行等问题,并会进行有关的计算。
3、掌握相似三角形、相似多边形的判定和性质,并能熟练运用它们进行证明或计算。
【知识讲解】
1、比例的性质:(1)基本性质:![]()
(2)合比性质:![]()
(3)等比性质:若![]() ,且
,且![]()
则![]()
注:(1)在![]() 中,d称为a、b、c的第四比例项。
中,d称为a、b、c的第四比例项。
(2)基本性质中,若两个比例的内项相等,即![]() 。此时称b为a、c的比例中项。
。此时称b为a、c的比例中项。
(3)要注意等比性质的使用条件:![]() ,掌握等比性质的证明方法。
,掌握等比性质的证明方法。
(4)已知C点把线段AB分成两条线段AC,BC(AC>BC),若AC是BC和AB的比例中项,则称C点把线段AB黄金分割,C叫线段AB的黄金分割点,此时
![]() 。
。
2、平行线分线段成比例定理及其推论
(1)三条平行线截两条直线,所得对应线段成比例
![]()
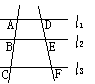
![]()
![]()
![]()
![]()
(2)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例;所截得的三角形与原三角形相似;所截得的三角形的三边与原三角形的三边对应成比例。
![]()
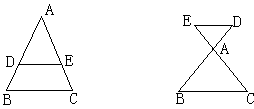
![]()
![]()
![]()
![]()
△ADE∽△ABC
![]()
(3)如果一条直线截三角形的两边(或其延长线)所截得的对应线段成比例,那么这条直线平行于三角形的第三边。
即在上面的“A”型图中或“X”型图中,若有被截两边AB、AC上的对应线段成比例,如
![]() ,
,![]() ,
,![]() 等,则可推出DE//BC,但要注意由
等,则可推出DE//BC,但要注意由![]() 推不出DE//BC。
推不出DE//BC。
说明:“A”型图和“X”型图在相似形一章中有着广泛的应用,希望同学们引起足够的重视。
3、相似三角形:对应角相等,对应边成比例的两个三角形。
(1)相似三角形的判定:
定理:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
判定定理:两角对应相等,两三角形相似;两边对应成比例且夹角相等,两三角形相似;三边对应成比例,两三角形相似;斜边和一条直角边对应成比例的两直角三角形相似;直角三角形被斜边上的高所分成的两个直角三角形都与原三角形相似。
(2)相似三角形的性质:
相似三角形的对应角相等,对应边成比例;
相似三角形中的对应线段(中线、角平分线、高等)之比等于相似比;
相似三角形的周长比等于相似比;
相似三角形的面积比等于相似比的平方。
4、相似多边形:若两个边数相同的多边形的对应角相等,对应边成比例。
(1)相似多边形的判定方法只有一种:即定义。
(2)相似多边形的性质类似于相似三角形的性质,对于相似多边形来说,其中的对应三角形也相似,相似比等于相似多边形的相似比。
说明:研究多边形的问题,常常把多边形分成若干个三角形,把求解多边形的问题转化为求解三角形的问题。
例1. 填空题
(1)若3x-4y=0,则![]() ,
,![]()
(2)△ABC的三边长为a、b、c,三边上的高为ha、hb、hc,若a:b:c=5:4:6,则
ha:hb:hc= _____.
(3)C是线段AB的黄金分割点,AC>BC,则![]() .
.
(4)若![]() ,则k= ______.
,则k= ______.
(5)如图,△ABC中,AD:DC=1:2,E为BD的中点,则BF:FC= ______.
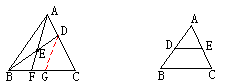 |
(6)如图,△ABC中,DE//BC,DE把△ABC分成面积相等的两部分,则![]()
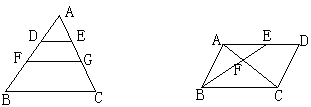 (7)已知如图,DE//FG//BC,AD:DF:FB=2:3:4,分别记△ADE,四边形DEGF,四边形FGCB的面积为S1、S2、S3,则S1:S2:S3=
______.
(7)已知如图,DE//FG//BC,AD:DF:FB=2:3:4,分别记△ADE,四边形DEGF,四边形FGCB的面积为S1、S2、S3,则S1:S2:S3=
______.
![]() (8) ABCD中,E为AB上一点,AE:ED=4:3,BE交AC于F,则S△AEF:S△ADC=____.
(8) ABCD中,E为AB上一点,AE:ED=4:3,BE交AC于F,则S△AEF:S△ADC=____.
[分析与解答](1)由比例的性质:
![]()
(2)由![]()
∴ ha:hb=b:a=4:5,hb:hc=c:b=6:4=3:2
∴ ha:hb:hc=12:15:10
(3)∵![]() ,
,![]()
∴![]()
(4)若a+b+c≠0,由等比性质得![]() ;
;
若a+b+c=0,则a+b=-c,![]()
∴![]() 或-1
或-1
说明:本题若不考虑等比性质的使用条件,则很容易漏掉k=-1
(5)作DG//AF交BC于G,则BF=FG,FG:GC=AD:DC=1:2,∴BF:FC=1:3
说明:求线段之比的问题,常可作平行线转化已知条件,从而得出结论。
(6)由条件得:![]() ,∴
,∴![]() ,
,![]()
(7)∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
说明:求两个三角形的面积之比,一定要注意两个三角形的内在联系,如等高、等底、相似等。
(8)利用相似三角形性质,可求得![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,∴S1:S2:S3=4:21:56
,∴S1:S2:S3=4:21:56
例2. 选择题:
(1)下列命题:
①有一对锐角相等的两个直角三角形相似
②有一角为100°的两个等腰三角形相似
③所有的菱形都相似
④两个正多边形一定相似
其中正确命题的个数有…………………………………………………………( )
A、1个 B、2个 C、3个 D、4个
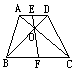 (2)如图,梯形ABCD中,AD//BC,AC、BD交于O,过O的直线分别交上、下底于E、F,则图中与
(2)如图,梯形ABCD中,AD//BC,AC、BD交于O,过O的直线分别交上、下底于E、F,则图中与![]() 的比值相等的比有……………( )
的比值相等的比有……………( )
A、4个 B、5个
C、6个 D、7个
![]() (3)如图,在 ABCD中,O1、O2、O3为对角线上三点,且BO1=O1O2=O2O3=O3D,
(3)如图,在 ABCD中,O1、O2、O3为对角线上三点,且BO1=O1O2=O2O3=O3D,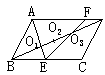 连结AO1并延长交BC于E,连结EO3并延长交AD于F,则AD:FD等于………( )
连结AO1并延长交BC于E,连结EO3并延长交AD于F,则AD:FD等于………( )
A、19:2 B、9:1
C、8:1 D、7:1
(4)如图,△ABC中,CE:EB=1:2,DE//AC,若△ABC的面积为S,则△ADE的面积为…………………………………………………………………………………( )
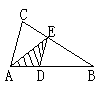 A、
A、![]() B、
B、![]()
C、![]() D、
D、![]()
(5)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,![]() ,则
,则![]() 等于……………………………………………………………………………( )
等于……………………………………………………………………………( )
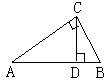 A、
A、![]() B、3:2
B、3:2
C、2:3 D、![]()
[分析与解答]
(1)①②正确,③④错误,故选(B)
(2)与![]() 相等的比有:
相等的比有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,故选(B)
,故选(B)
(3)由条件知![]() ,
,![]() ,∴
,∴![]() ,故选(B)
,故选(B)
(4)∵![]() ,∴
,∴![]() ,选(A)
,选(A)
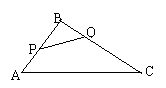 (5)C∵△CDB∽△ACB,∴
(5)C∵△CDB∽△ACB,∴![]() ,选(C)
,选(C)
例3、如图,在△ABC中,AB=8厘米,BC=16厘米,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以4厘米/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟△PBQ与△ABC相似?
[分析与解答] △PBQ与△ABC相似,顶点之间有两点可能的对应关系,一种是△PBQ∽△ABC,另一种是△PBQ∽△CBA,所以我们要分两种情况加以解决。
解:设P、Q同时出发后,经x秒,△PBQ与△ABC相似,则AP=2x,BQ=4x,PB=8-2x。
(1)若△PBQ∽△ABC,则![]() ,即
,即![]() ∴x=2;
∴x=2;
(2)若△PBQ∽△CBA,则![]() ,即
,即![]() ∴
∴![]() 。
。
答:经过2秒或![]() 秒,△PBQ与△ABC相似。
秒,△PBQ与△ABC相似。
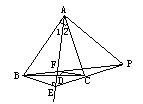 例4. △ABC中,AD平分∠BAC,BE⊥AD于E,CF⊥AD于F,EC、BF的延长线交于P。
例4. △ABC中,AD平分∠BAC,BE⊥AD于E,CF⊥AD于F,EC、BF的延长线交于P。
求证:AP∥CF
分析:欲证AP∥CF,需证在EA、EP上有对应线段成比例。
证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠AFC=90°,BE∥CF又∵∠1=∠2,∴△ABE∽△ACF,∴![]() ,∵BE//CF,∴
,∵BE//CF,∴![]() ,
,
∴![]() ,∴AP∥CF
,∴AP∥CF
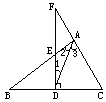 例5. Rt△ABC中,∠BAC=90°,D为BC中点,过D作BC的垂线分别交AB于E,CA的延长线于F。
例5. Rt△ABC中,∠BAC=90°,D为BC中点,过D作BC的垂线分别交AB于E,CA的延长线于F。
求证:AD2=DE·DF
分析:把要证的结论改成比例式![]() ,通过三点定位找出两个三角形:△ADE和△FDA,若能证明这两个三角形中除∠1外还有一对角对应相等,即可得△ADE∽△FDA,从而证明结论成立。
,通过三点定位找出两个三角形:△ADE和△FDA,若能证明这两个三角形中除∠1外还有一对角对应相等,即可得△ADE∽△FDA,从而证明结论成立。
证明:在△ABC中,∠BAC=90°,BD=DC
∴∠2+∠3=90°,DA=DC,∴∠C=∠3
∵FD⊥BC,∴∠C+∠F=90°,∴∠F=∠2,又∵∠1=∠1,∴△ADE∽△FDA
∴![]() ,∴
,∴![]()
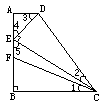 例6. 梯形ABCD中,AD∥BC,∠B=90°,E、F为AB上两点,使∠DEC=90°,∠1=∠2
例6. 梯形ABCD中,AD∥BC,∠B=90°,E、F为AB上两点,使∠DEC=90°,∠1=∠2
求证:BF=AE
证明:∵∠1=∠2,∠B=∠CED=90°
∴△CBF∽△CED,∴![]() ,∵AD∥BC,∠B=90°,∴∠A=90°∴∠3+∠4=90°,∵∠DEC=90°,∴∠4+∠5=90°,∴∠3=∠5,又∵∠A=∠B=90°∴△ADE∽△BEC,∴
,∵AD∥BC,∠B=90°,∴∠A=90°∴∠3+∠4=90°,∵∠DEC=90°,∴∠4+∠5=90°,∴∠3=∠5,又∵∠A=∠B=90°∴△ADE∽△BEC,∴![]() ,∴
,∴![]() ,∴AE=BF.
,∴AE=BF.
说明:利用比例线段证明线段相等,通常这样处理:要证线段a=b,只要能证出
![]() 和c=d即可。
和c=d即可。
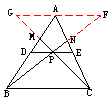 例7. 已知:DE是△ABC的中位线,P为DE上一点,BP、CP的延长线分别交AC、AB于N、M。
例7. 已知:DE是△ABC的中位线,P为DE上一点,BP、CP的延长线分别交AC、AB于N、M。
求证:![]()
分析:要证几个比的和(差)为常数,通常需将这几个比转化为分母相同的比,而后再进行加减运算。本题中利用已有的平行线DE//BC,无法将两个比转化,所以需要添加适当的辅助线。
证明:过A作GF//BC交BN、CM的延长线于F、G
∴![]() ,
,![]()
∴![]()
∵AG//PE,AE=EC,∴CP=PG,
同理可证:BP=PF
又∵∠BPC=∠FPG,∴△BPC≌△FPG
∴BC=FG,∴![]()
说明:若需证几个比的积为常数,则通常把几个比化为能约分的比,而后再进行乘积运算。
【一周一练】
一、填空题:(每小题2分,计16分)
1、(2002·龙沿)若![]() (a≠0),则
(a≠0),则![]() 。
。
2、(2002·福州)已知线段a=4cm,b=9cm,则a、b的比例中项c为_____cm。
3、(2002·临沂)用一桶配农药给果树除虫,桶高0.7m,桶内有一斜放的木棒,一端在桶底,另一端在桶盖小口处,抽出木棒量出木棒的总长为1m,上面浸有农药部分长为0.7m,则桶内药液的高度为 m。
4、(2002·南京)下列命题:(1)所有的等腰三角形都相似;(2)所有的等边三角形都相似;
(3)所有的等腰直角三角形都相似;(4)所有的直角三角形都相似。其中真命题的序号是 (把所有真命题的序号都填上)
5、如图,△ABC中,∠ACB=90°,AC=7,BC=3,CM、CH分别是中线和高,则S△ACM:S△BCM= ______;S△ACH:S△BCM= _____.
6、(2000·河南)如图,在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,那么CD= 。

7、如图,已知M是平行四边形ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与平行四边形ABCD的面积比为______。
8、如图,要把一个边长为a的正方形剪成一个最大的正八边形,须剪去四个全等的等腰直角三角形(图中阴影部分),其中一个等腰直角三角形的直角边长等于_______。
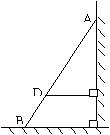 二、选择题:(每小题3分,计30分)
二、选择题:(每小题3分,计30分)
1、(2001·吉林)如图,AB是斜靠在墙壁上的长梯,梯脚B跟距墙1.6米,梯上点D距墙1.4米,BD长0.55米,则梯子的长为( )
A、3.85米 B、4.00米
C、4.40米 D、4.50米
 2、(2001·无锡)如图,E平行四边形ABCD的边BC的延长线上一点,连结AE交CD于F,则图中共有相似三角形( )
2、(2001·无锡)如图,E平行四边形ABCD的边BC的延长线上一点,连结AE交CD于F,则图中共有相似三角形( )
A、1对 B、2对
C、3对 D、4对
3、一个钢筋三角架三边长分别为20cm、50cm、60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A、一种 B、两种
C、三种 D、四种或四种以上
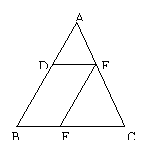 4、(2000·黄冈)如图,已知DE//BC,EF//AB,现得下列结论①
4、(2000·黄冈)如图,已知DE//BC,EF//AB,现得下列结论①![]() ;②
;②![]() ;③
;③![]() ④
④![]() ,其中正确比例式的个数有( )
,其中正确比例式的个数有( )
A、4个 B、3个
C、2个 D、1个
5、梯形ABCD中,AB//DC,EF为其中位线,则△AEF的面积与梯形ABCD的面积之比为( )
A、1:3 B、1:4 C、2:5 D、3:5
6、(2002·北京东城区)P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有( )
A、2条 B、3条 C、4条 D、5条
 7、(2001·黑龙江)如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF等于( )
7、(2001·黑龙江)如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF等于( )
A、4:10:25 B、4:9:25
C、2:3:5 D、2:5:25
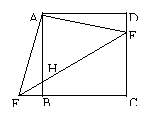 8、(2001·黑龙江)如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连结EF交AB于H,则下列结论错误的是( )
8、(2001·黑龙江)如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连结EF交AB于H,则下列结论错误的是( )
A、AE⊥AF
B、EF:AF=![]()
C、AF2=FH·FE D、FB:FC=HB:EC
 9、(2002·嘉兴)如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动。现有一块石头,要使其滚动,杠杆的B端必须向上翘起10cm,已知杠杆的动力臂AC与阻力臂BC之比为5:1,则要使这块石头滚动,至少要将杠杆的A端向下压( )
9、(2002·嘉兴)如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动。现有一块石头,要使其滚动,杠杆的B端必须向上翘起10cm,已知杠杆的动力臂AC与阻力臂BC之比为5:1,则要使这块石头滚动,至少要将杠杆的A端向下压( )
|
C、50cm D、10cm
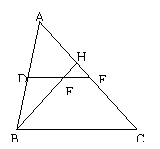 10、(2001·北京东城区)如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则AH:HE等于( )
10、(2001·北京东城区)如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则AH:HE等于( )
A、1:1 B、2:1
C、1:2 D、3:2
三、计算或证明题:(每小题9分,计54分)
1、(2001·山西)在方格纸中每个小格的顶点叫做格点。以格点连线为边的三角线叫做格点三角形。请你在如图所示的10×10的方格纸中,画出两个相似但不全等的格点三角形,并加以证明。要求:所画三角形是钝角三角形,并标明相应字母。

2、(2002·吉林)将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,回答下列问题:(1)图中共有多少个三角形?把它们一一写出来;(2)图中有相似(不含全等)三角形吗?如果有,就把它们一一写出来.

3、(2002·威海)如图,AD、CE是△ABC的高
(1)求证:△BDE∽△BAC;
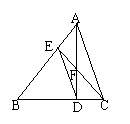 (2)若AC=10,cosB=
(2)若AC=10,cosB=![]() ,求DE的长.
,求DE的长.
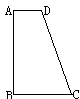 4、如图,在梯形ABCD中,AD//BC,∠A=90°,AB=7,AD=2,BC=3,试在边AB上确定点P的位置,使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似。
4、如图,在梯形ABCD中,AD//BC,∠A=90°,AB=7,AD=2,BC=3,试在边AB上确定点P的位置,使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似。
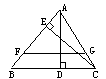 5、△ABC中,AD⊥BC于D,CE⊥AB于E,在AB上截取AF=AD,作FG∥BC交AC于G。
5、△ABC中,AD⊥BC于D,CE⊥AB于E,在AB上截取AF=AD,作FG∥BC交AC于G。
求证:FG=CE
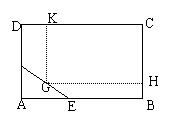 6、某房地产公司要在一地块中(图中矩形ABCD)上,规划建造一个小区公司(矩形GHCK),为了使文物保护区△AEF不被破坏,矩形公园的顶点,G不能在文物保护区内。已知AB=200m,AD=160m,AE=60m,AF=40m.
6、某房地产公司要在一地块中(图中矩形ABCD)上,规划建造一个小区公司(矩形GHCK),为了使文物保护区△AEF不被破坏,矩形公园的顶点,G不能在文物保护区内。已知AB=200m,AD=160m,AE=60m,AF=40m.
(1)当矩形小区公园的顶点G恰是EF的中点时,求公园的面积;
(2)当G在EF上什么位置时,公园面积最大?
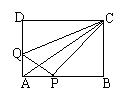
7、(2002·河北)如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6)那么
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积,提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
 |
【一周一练答案】
一、1、5, 2、6 3、0.49 4、(2)(3)
5、1:1,49:9 6、4
7、![]() 8、
8、![]()
二、1、C 2、C 3、B 4、B 5、B
6、C 7、A 8、C 9、C 10、B
三、
1、略
2、(1)共有7个三角形,分别是△ABD、△ABE、△ABC、△ADE、△ADC、△AEC、△AFG
(2)有相似三角形,它们是△ADE∽△BAE∽△CDA
3、(1)先证明△BCE∽△BAD,∴![]() ,又∠B=∠B∴△BDE∽△BAC
,又∠B=∠B∴△BDE∽△BAC
(2)DE=6
4、(1)若△APD∽△BPC,则![]() ∴
∴![]() ,AP=
,AP=![]()
(2)若△APD∽△BCP,则![]() ∴
∴![]() ,AP=1或6
,AP=1或6
∴当AP的长为1或6或![]() 时,以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似。
时,以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似。
5、证明:∵FG//BC∴![]() ,∵∠BEC=∠BDA=90°,∠B=∠B
,∵∠BEC=∠BDA=90°,∠B=∠B
∴△BDA∽△BEC,∴![]() ,又∵AF=AD,∴
,又∵AF=AD,∴![]() ,∴
,∴![]() ,
,
∴CE=FG
6、延长HG、KG分别交AD、AB于M、N。
(1)当G是EF的中点时,由三角形中位线定理,得
![]() 。∴S矩形KGHC=HG·KG=(200-30)(160-20)=23800(m2);
。∴S矩形KGHC=HG·KG=(200-30)(160-20)=23800(m2);
(2)设MG=x,则GH=200-x。∵MG∥AE,∴△FMG∽△FAE。
∴![]() MA=FA-FM=40-
MA=FA-FM=40-![]() (0≤x≤60).
(0≤x≤60).
∴S矩形KGHC=HG·KG=(200-x)[160-(40-![]() )]=
)]=![]()
∴当x=10(m)时,S矩形KGHC最大。
7、(1)t=2s,△QAP为等腰直角三角形
(2)SQAPC=36,∴P、Q两点在运动的过程中,四边形QAPC的面积保持不变
(3)分两种情况:若△QAP∽△ABC,t=1.2s;若△PAQ∽△ABC,t=3s