一次函数 反比例函数 不等式复习题 班级______ 姓名____________
一.填空题
1.点A在
轴右侧，距轴6个单位长度，距
轴8个单位长度，则A点的坐标是 ，A点离开原点的距离是
。
2.点（-3，2），（a,a+1）在函数
的图像上，则
3.函数
与x轴的交点是 ，与y轴的交点是 。与两坐标轴围成的三角形面积是
。
4.已知y与4x-1成正比例，且当x=3时，y=6，写出y与x的函数关系式 。
5、某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费0.5元，超计划部分每吨按0.8元收费。
（1） 写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式①用水量小于等于3000吨 ；②用水量大于3000吨 。
（2） 某月该单位用水3200吨，水费是 元；若用水2800吨，水费 元。
（3） 若某月该单位缴纳水费1540元，则该单位用水 吨.
6. 用不等式表示：x的3倍与1的差不大于2与
的和的一半，得__ ___
7.直线
与
平行，且经过（2，1），则k= ,b= .
二、选择：
8.下面哪个点不在函数
的图像上（ ）
A.（-5，13） B.（0.5，2） C（3，0） D（1，1）
9.下列函数中，y随x的增大而减小的有（ ）A.1个B.2个C.3个D.4个
①y=-2x+1 ②
③
④
10．在同一直角坐标系中，函数y=kx-k与y=
（k≠0）的图象大致是(
)
A B C D
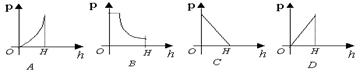
11、已知圆柱的侧面积是100
，若圆柱底面半径为
（），高线长为
（
），则关于的函数的图象大致是（ ）
三.解答题
12. 在同一坐标系中作出， y=2x+1,y=3x ,y=4x-3的图像
在上述三个函数的图像中，哪一个函数的值先达到30？
13、解不等式组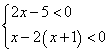
，并把解集在数轴上表示出来。
14.某市自来水公司按如下标准收取水费，若每户每月用水不超过5m3则每立方米收费1.5元；若每户每月用水超过5m3,，则超出部分每立方米收费2元。小颖家某月的水费不少于15元，那么她家这个月的用水量至少是多少？
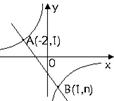15、如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的的
取值范围
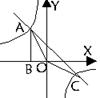16、如图，Rt△ABO的顶点A是双曲线
与直线
在第二象限的交点，AB⊥轴于B且S△ABO=
（1）求这两个函数的解析式
（2）求直线与双曲线的两个交点A，C的坐标和△AOC的面积。
17 .如图，lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
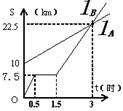（1）B出发时与A相距 千米。
（2）走了一段路后，自行车发生故障，进行修理，所用的时间是 小时。
（3）B出发后 小时与A相遇。
（4）若B的自行车不发生故障，保持出发时的速度前进， 小时与A相遇，相遇点离B的出发点 千米。在图中表示出这个相遇点C。
（5）求出A行走的路程S与时间t的函数关系式。（写出过程）
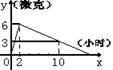18、某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药后2小时时血液中含药量最高，达每毫升6微克（1微克=10―3毫克），接着逐步衰减，10小时时血液中含药量为每毫升3微克，每毫升血液中含药量y微克随时间x小时的变化如图所示，当成人按规定剂量服药后，
（1）分别求出≤2和≥2时
与之间的函数关系式
（2）如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的，那么这个有效时间是多长？