|
|
学科：数学 |
| 教学内容：一次函数的图像和性质 |
【基础知识精讲】
一、一次函数的图像
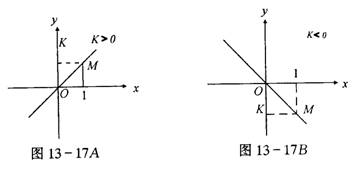
1.正比例函数y=kx(k≠0,k是常数)的图像是经过O(0，0)和M(1，k)两点的一条直线(如图13-17).(1)当k＞0时，图像经过原点和第一、三象限；(2)k＜0时，图像经过原点和第二、四象限.
2.一次函数y=kx+b(k是常数，k≠0)的图像是经过A(0,b)和B(-
，0)两点的一条直线，当kb≠0时，图像(即直线)的位置分4种不同情况：
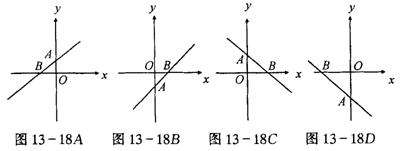
(1)k＞0,b＞0时，直线经过第一、二、三象限，如图13-18A
(2)k＞0,b＜0时，直线经过第一、三、四象限，如图13-18B
(3)k＜0,b＞0时，直线经过第一、二、四象限，如图13-18C
(4)k＜0,b＜0时，直线经过第二、三、四象限，如图13-18D
3.一次函数的图像的两个特征
(1)对于直线y=kx+b(k≠0),当x=0时,y=b即直线与y轴的交点为A(0,b),因此b叫直线在y轴上的截距.
(2)直线y=kx+b(k≠0)与两直角标系中两坐标轴的交点分别为A(0，b)和B(-，0).设直线与x的夹角为α，则tgα=
=k，由于角α：0＜α＜90°，tgα＞,因此k=tgα.
4.一次函数的图像与直线方程
(1)一次函数y=kx+b(k≠0)的图像是一条直线，因此y=kx+b(k≠0)也叫直线方程.但直线方程不一定都是一次函数.
(2)与坐标轴平行的直线的方程.
①与x轴平行的直线方程形如：y=a(a是常数).a＞0时，直线在x轴上方；a=0时，直线与x轴重合；a＜0时，直线在x轴下方.(如图13-19)
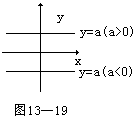
②与y轴平行的直线方程形如x=b(b是常数)，b＞0时，直线在y轴右方，b=0时，直线与y轴重合；b＜0时，直线在y轴左方，(如图13-20).
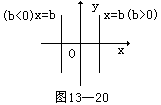
二、两条直线的关系
1.与坐标轴不平行的两条直线l1:y1=k1x+b1,l2:y2=k2x+b,若l1若l2相交，则k1≠k2;若k1≠k2，则l1与l2不平行，其交点是联立这两条直线的方程，求得的公共解.
三、一次函数的增减性
1.增减性 如果函数当自变量在某一取范围内具有函数值随自变量的增加(或减少)而增加(或减少)的性质，称为该函数当自变量在这一取值范围内具有增减性，或称具有单调性.
2.一次函数的增减性
一次函数y=kx+b在x取全体实数时都具有如下性质：
(1)k＞0时，y随x的增加而增加；
(2)k＜0时，y随x的增加而减小.
3.待定系数法求一次函数的解析式：
若已知一次函数的图像(即直线)经过两个已在点A(x1，y1)和B(x2，y2)求这个一次函数的解析式，其方法和步骤是：
(1)设一次函数的解析式：y=kx+b(k≠0)
(2)将A、B两点的坐标代入所设函数的解析式，得两个方程：y1=k1x1+b①y2=k2x2+b2②
(3)联立①②解方程组，从而求出k、b值.
这一先设系数k、b，从而通过解方程求系数的方法以称为待定系数法.
【重点难点解析】
例1 已知一次函数y=(m+3)x+(4-n),(1)m为何值时，y随x的增大而减小；(2)n为何值时，函数的图像与y轴的交点x轴下方；(3)m、n为何值时，函数图像与y=x+2的图像平行.
解：(1)当m+3＜0,即m＜-3时，y随x的增大而减小；
(2)当4-n＜0,即n＞4时，函数的图像与y轴的交点在x下方；
(3)当m+3=1且4-n≠2时，即m=-2, n≠2时，函数的图像是一条与y=x+2平行的直线.
例2 当a、b＞0，ac＜0，直线ax+by+c=0不通过哪个象限.
解：∵b≠0 ∴由原函数式变形得：
y=-
x-
∴ab＞0 ∴-＜0
又∵ac＜0,∴-＞0
直线ax+by+c=0不通过第三象限.
例3 直线l1:y1=k1x+b1 与y=2x平行且通过A(3，4)，直线l2:y2=k2x+b2通过B(1，3)，C(-1，5)，求l1和l2的解析式.
解：∵y1=k1x+b1与y=2x平行且通过A(3，4)
∴
解这个方程组得：
∴l1的解析式为:y=2x-2
∵y2=k2x+b2通过B(1，3)和C(-1，5)两点，将两点的坐标代入解析式得：
∴l2的解析式为：y=-x+4
例4 已知一个正比例函数和一个一次函数，它们的图像都经过P(-2，1)，且一次函数在y轴上的截距为3.(1)求这两个函数的解析式；(2)在同一坐标系中，分别画出两个函数的图像；(3)求这两个函数的图像与y轴围成的三角形的面积.
解：(1)设正比例函数和一次函数的解析式分别为y=k1x和 y=k2x+b.由y=k1x过点(-2，1)得1=-2k1 ∴k1=-
由y=k2x+b过点(-2，1)，截距为3 得：b=3
-2k2+b=1 解得：k2=1 b=3
(2)过点O(0，0)、P(-2，1)两点画一条直线，即得函数y=-x的图像.经过A(0，3)和P(-2，1)画一条直线即得y=x+3的直线，如图13-21
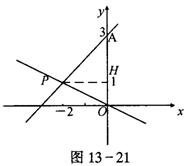
(3)直线y=x+3与y轴交于点A(0，3)过P作PH⊥y轴，则OA=3，PH=-2=2，而函数与y轴所围成的三角形面积即是△APO的面积.
S△APO=·AO·PH
=×3×2=3
例5 已知y-(m-3)与x(m是常数)成正比例，且 x=6时，y=1；x=-4时， y=-4.(1)求y与x之间的函数关系式；(2)在直角坐标系中，画出这个函数的图像；(3)求出这个函数的图像与坐标轴的两个交点之间的距离.
解：∵y-(m-3)与x成正比例
∴可设y-(m-3)=kx,即y=kx+m-3①
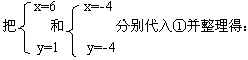
故所求函数关系式为：y=x-2
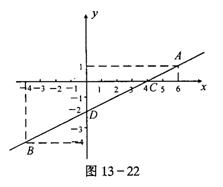
(2)经过A(6，1)和B(-4，-4)画直线即是函数y=x-2的图像.如图13-22
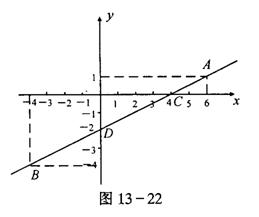
(3)当x=0时：y=×0-2=-2
当y=0时，0=x-2 x=4
∴C(4，0)，D(0，-2)
CD=
综上所述5例可见，本节重点为：①根据直线所通过的点的条件求直线方程；②根据直线方程求作直线的图像；③根据增减性、截距求直线方程；④根据两直线的位置关系求直线方程；本节的难点是求直线围成的图形的面积.解决重难点的方法是运用待定系数法和数形结合的方法.
【难题巧解点拨】
例6 已知函数y=x-a+x+19+x-a-96，其中a为常数，且满足19＜a＜96,当自变量x的取值范围为a≤x≤96时，求y的最大值.
解：∵19＜a＜96,a≤x≤96
∴x-a≥0,x+19＞10,x-a-96＜0则y=x-a+x+19+a+96-x=115+x
函数y=15+x是一次函数，其增减性表明y随x的增大而增大.
∴在a≤x≤96的x取值范围内，当x=96时，y取最大值，即：
ymax=96+115=211
说明：含绝对值的函数首先要讨论绝对值的式子的正负性质，再根据绝对值定义化简，从而得到一次函数；讨论在某一自变量的取值范围内最大值或最小值要根据一次函数的性质和自变量x范围的两端点取值来求.
例7 如图13-23在平面直角坐标系中，点O′的坐标为(0，3)，⊙O′与y轴交于原点O和点A，又B、C、E三点的坐标分别为(0，-2)、(4，0)、(x，0)，且0＜x＜4.(1)求点A的坐标；(2)当点E在线段OC上移动时，直线BE与⊙O′有哪几种位置关系？(3)求出直线BE与⊙O′每种位置关系时，x的取值范围.
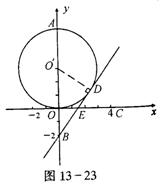
分析：直线与圆有三种位置关系，从直线与圆相切这种特殊情形，用运动变化的观点寻求结论成立的条件是解本题的关键.
解：(1)∵O′(0，3) ∴⊙′的半径为：
OO′=3，∴OA=2·OO′=2×3=6，∴A(0，6)
(2)∵点B在⊙O′外，BE与⊙O′有三种位置关系：相离、相切、相交；
(3)当直线BE与⊙O′相切于D点时，连结O′D，则△O′BD是Rt△.
O′D=3, O′B=5,BD=4,OB=2,OE=x
∵△O′BD∽△EBO
∴
即
，解得：x=
故当＜x＜4时，直线BE与⊙O′相离；当x=时，直线BE与⊙O′相切.
当0＜x＜时，直线BE与⊙O′相交.
例8 如图13-24，某航空公司托运行李的费用与托运行李重量的关系为一直线，由图中可知行李的重量不超过多少公斤，就可以免费托运？
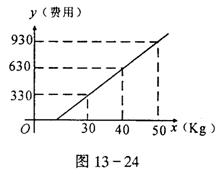
解：设直线方程为：y=kx+b (k、b是常数，k≠0)
由图可知：x=20时，y=330；x=40时，y=630;把x,y的对应取值代入直线方程，得：
解这个方程组，得：k=30,b=-570
∴直线方程为:y=30x-570
若y=0时，30x-570=0, ∴x=19
答：只要行李重量不超过19公斤时，就可免费托运.
【命题趋势分析】
由于一次函数是最基本的函数内容，是初中重点之一，在实际中应用十分广泛，因此是中考热点考题.有关一次函数考试主要是概念、图像、性质三个基本内容和待定系数法、数形结合法两种数学方法.
【典型热点考题】
例9 填空题：已知直线l:y=-3x+2，现在4个命题：①点P(1，-1)在直线l上；②若直线l与x轴、y轴分别交于A、B两点，则AB=
；③若点M(
，1)，N(a、b)都在直线l上，且a＞,则b＞1;④若点Q到两坐标轴的距离相等，且点Q在l上，则点Q在第一或第四象限.
其中正确的命题是 .(注意：在横线上填上你认为正确的命题序号)(2000年厦门市中考题)
分析：检验①：只需将x=1,y=-1代入函数式看是否适合，当x=1时，y=-3+2=-1,即P(1，-1)在直线y=-3x+2上，①命题正确；检验②；当y=0时，求得x=
,即A(，0)，当x=0时，y=2，即B(0，2)，∴AB=
，命题②正确；检验③，若M(，1)，N(a,b)都在y=-3x+2上，根据直线的性质，k=-3＜0,y随x的增加而减小，∴a＞时，应该有b＜0,因此b＞1错误，即命题③错误；检验④，∵Q到两坐标轴的距离相等，设Q(m、n)，则m=n,且n=-3m+2,由此解得：
或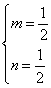
因此Q点在第一或第四象限，命题④正确.
因此，选①、②、④填空.
例10 某居民小区按照分期付款的形式福利售房，政府给予一定的贴息，小明家购得一套现价为120000元的房子，购房时首期(第一年)付款30000元，从第二年起，以后每年应付房款5000元与上一年剩余欠款利息的和，设剩余欠款年利率为0.4%.(1)若第x(x≥2)年小明家交付房款y元，求年付款y(元)与x(年)的函数关系式；(2)将第三年，第十年应付房款填入下列表格中：(2000年大连市中考题)
| 年份 | 第一年 | 第二年 | 第三年 | …… | 第十年 |
| 交房款(元) | 30000 | 5360 |
| …… |
|
分析：首期付款后共余120000-30000=90000元房款，以后每年付款应为5000，与上一年所欠余款×0.4%，即余款的利息之和.
解：(1)y=5000+[90000-5000(x-2)] ×0.4%
=5400-20x(x≥2)
(2)当x=3时，y=5340，当 x=10 时，y=5200，
因此第三年应付款5340元，第十年应付款5200元.
例11 已知直线x-2y=-k+6和x+3y=4y+1，若它们的交点在第四象限内，(1)求k的取值范围，(2)若k为非负整数，点A的坐标为(2，0)，点P在直线x-2y=-k+6上，求使△PAO为等腰三角形的点P的坐标.(2000年西安市中考题)
解：(1)依题意：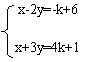
解这个方程组，得：x=k+4,y=k-1
∵两直线的交点在第四象限
∴k+4＞0,且k-1＜0
解不等式组得：-4＜k＜1
(2)∵k为非负整数，∴k=0
∴直线x-2y=-k+6即为：y=
-3
设P(a，b)为直线y=-3上一点，作PE⊥x轴，垂足为E，若使PO=PA，则应有OE=AE，即E(1，0)
∵a=1,∴b=-
∴P1(1,- )
若使PO=OA=2，则a2+b2=4,a2+(a-3)2=4,
a2-3a+5=0,
△=9-25＜0此方程无解.
若使PA=OA=2，则(2-a)2+b2=4,(2-a)2+(a-3)2=4,
∴a2-7a+9=0,a1=2,a2=
,当a1=2时，b1=-2，当a2=时 ,b2=-
.
∴P2(2,-2)或P3(，)
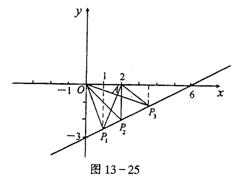
综合上所述，点P的坐标为(1，-)，(2，-2)，(，-)如图13-25.
【同步达纲练习】(时间：45分钟，满分：100分)
一、选择题(10分×6=60分)
(1)一次函数y=kx+b的图像经过点(m,-1)和点(1,m)，其中，m＜-1,则k和b满足的条件是( )
A.k＜0,b＜0 B.k＞0,b＞0 C.k＜0,b＞0 D.k＞0,b＜0
(2)若一次函数y=(1-2k)x-k(x为自变量)的函数值y随x的增大而增大，且此函数的图像不经过第二象限，则k的取值范围是( )
A.k＜
B.k＞0
C.0＜k＜ D.k＜0或k＞
(3)当mn＜0 mp＞0时，一次函数y=
的图像不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(4)一次函数y=kx+b的图像如图13-26,那么k、b应满足的条件是( )
A.k＞0,b＞0 B.k＞0,b＜0 C.k＜0,b＞0 D.k＜0,b＜0
(5)已知函数y=
的图像经过点(-1，1)，则函数y=kx+3的图像是( )
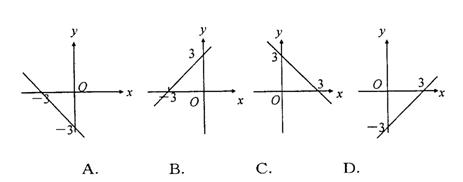
(6)直线y=kx+b与直线 y=-x垂直，并且经过点(-1，1)，那么直线y=kx+b的解析式为( )
A.y=-x-2 B.y=x+2 C.y=x-2 D.y=-x+2
二、解答题(10分×3=30分)
(7)已知一次函数y=(3-k)x+2k+1.①如果它的图像经过(-1，2)点，求k的值；②如果它的图像经过第一、二、四象限，求k的取值范围.
(8)已知y+b与x-1(其中b是常数)成正比例.①证明：y是x的一次函数；②若这个一次函数的图像经过点(，0)，且与坐标轴在第一象限内围成的三角形的面积为
，求这个一次函数，并画出它的图像.
(9)已知一次函数y=(p+3)x+(2-q).①p为什么实数时y随x的增大而增大？②q为什么实数时，函数图像与y轴的交点在x轴的上方；③p、q为什么实数时，函数的图像过原点？
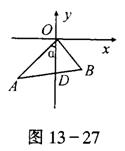
(10)如图13-27，在直角坐标系中，点A(x1，-3)在第三象限，点B(x2,-1)在第四象限，线段AB与y轴交于点D，∠AOB=90°，①当x2=1时，求图像经过A、B的一次函数的解析式；②当△OAB的面积等于9时，设∠AOD=α，求sinα·cosα的值.
【素质优化训练】
一个水池的容积是100m3,现存水20m3,今要灌满水池，已知进水管的流量是每小时8m3,写出水池的水量υ与进水时间t之间的函数关系式，并画出图像.
【生活实际应用】
某商场计划投入一笔资金采购一批紧俏商品，经过市场调查发现，如果月初出货，可获利15%，并可用本和利再投资其它商品，到月末又可获利10%；如果月末出售可获利30%，但要付出仓储费用200元，请问根据商场的资金状况，如何购销获利最多？
【知识探究学习】
求直线方程的几种方法：
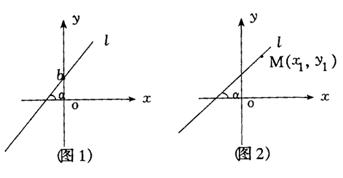
1.如图1，若l与x轴的夹角为α(0＜α＜90)，直线与y轴交于点(0，b),则直线l方程即为：
y=tgα·x+b
2.若l与x的夹角为α(0＜α＜90)，且经过点M(x1,y1)，如图2，则直线l的方程即可写为：
3.若l经过A(x1,y1)，B(x2,y2),则直线l的方程即可写为：
参考答案：
【同步达纲练习】
一、A C D D C B
二、(7)k=
,k＞3,(8)①y=kx-(k+b)(k≠0)；②y=-2x+5;(9)①P＞-3,②q＜2,③p≠3且q=2;(10)①y=x-;②sinα·cosα=
【素质优化训练】
v=20+8t(0≤t≤10)
【生活实际应用】
设商场投资x元，在月初出售，到月末可获得y1元，在月末出售可获利y2元.
y1=0.265x，y2=0.3x-700
(1) 当y1=y2时,x=20000
(2) y1＜y2时，x＞20000
(3) y1＞y2时，x＜2000